Eğik düzlem nedir? Dinamik soruları ve çözümleri

Dinamik deyince aklımıza hareketin sebebinin anlaşılması gelmesi gerektiğini öğrenmiştik. Şimdi eğik düzlem üzerindeki bir cismin hareketini inceleyeceğiz. Eğik düzlem, bir yüzeyin yataya belli bir açı yapacak şekilde yerleştirilmesiyle elde edilir. Örneğin, finüküler bir eğik düzlemdir, inşaatlarda el arabalarını rahat ilerletmek için tahtaları yokuş olacak şekilde yerleştirilmesi eğik düzlem örneklerindendir.

Bu yazıda eğik düzlemde serbest bırakılan bir cismin hareketini inceleyeceğiz. Aşağıdaki resimde, bir karton kutunun bir kenarı klasörlerin üstüne yerleştirerek diğeri yere bırakılarak bir eğik düzlem elde edilmiş. Üstüne de bir tahta silgisi konulmuş.

Aşağıdaki resimde bunun şematik hali gösteriliyor, yandan kesit alıp bakıyoruz. Fizikte bunu çok sık yapıyoruz, gerçek bir durumun basitleştirilmiş resmini çiziyoruz.

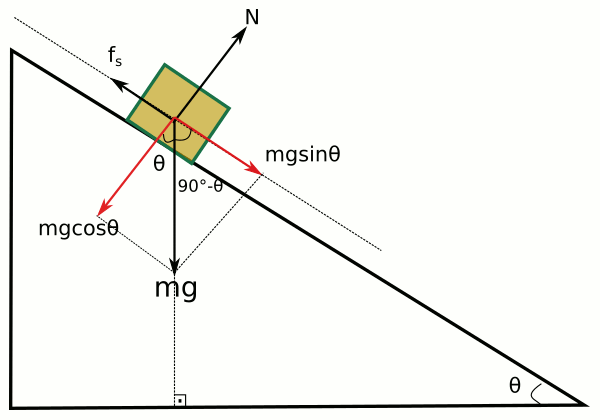
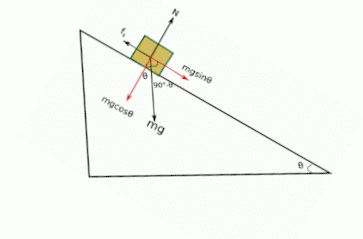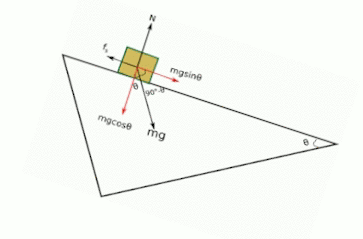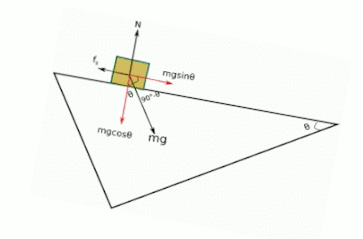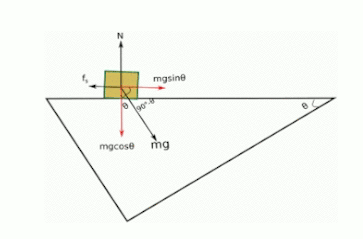
Yukarıdaki resimde bir tahta takozu eğik düzleme koymuşlar. Bu takoz nasıl hareket eder sorusuna cevap arıyoruz. Newton’un hareket kanunları hareketi açıkladığına göre, takoz nasıl hareket eder sorusuna bu kanunları kullanarak yanıt vereceğiz. Cismin üzerindeki kuvvetleri göstermek için serbest cisim diyagramını çizmemiz gerekecek, aslında yukarıdaki cisimde çizilmiş durumda. Şimdi kuvvetlerin bileşenlerini bulalım.

1. Eğik düzlemin yatayla yaptığı açı θ, eğik düzlemin kendisi bir dik üçgen şeklinde.
2. Cismin ağırlığı (mg, kütlesiyle yer çekimi ivmesinin çarpımı), -y yönünde (yere dik). Ağırlık kuvvetinin doğrultusunu alırsanız (resimdeki yere dik yatay kesikli çizgi), bunun da eğik düzleme benzer bir dik üçgen oluşturduğunu görebilirsiniz.
3. Dik üçgenin iç açılarının toplamı 180° olduğuna göre ağırlık ile ağırlığın eğik düzleme paralel olan bileşeni arasındaki açının (β açısı diyelim) 90° – θ olduğunu görebilirsiniz. (180° = 90° + θ + β, β = 180° – 90° – θ, β = 90° – θ)
4. Ağırlığın eğik düzleme dik olan bileşeninin açısının (α diyelim bu açıya) da bu durumda θ olması gerekir. Çünkü, ağırlık vektörünü dik bileşenlerine ayırıyoruz. (α + β = 90°, β = 90° – θ, α + 90° – θ = 90°, α = θ).
5. Öyleyse ağırlığın eğik düzleme paralel bileşeni m\vec{g}sin \theta ve eğik düzleme dik bileşeni m\vec{g}cos \theta olur.

Şimdi analizimize devam etmek için bu şekli biraz daha basitleştirelim. Bunun en kolay yolu koordinat sistemini çevirmek. Yani tüm sistemi (eğik düzlemi, takozu ve yeri) saat yönünün tersine doğru θ kadar döndüreceğiz.

Koordinatları çevirdiğimiz zaman eğik düzlem sistemi aşağıdaki gibi görünüyor.

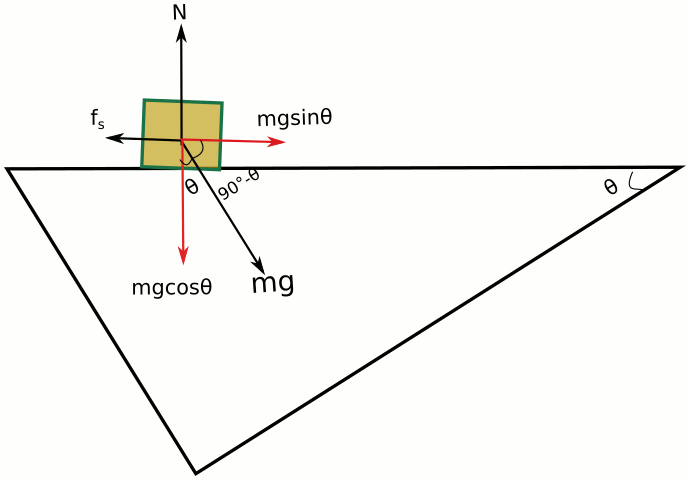
Yukarıdaki resimde koordinat sisteminin döndürülmüş halini görüyoruz, bu tanıdık bir şekil, x ve y eksenleri bizim alışık olduğumuz hale geldi, +x sağa, +y yukarı doğru. Şimdi yatay ve düşey düzlemlere Newton’un hareket kanunlarını uygulayalım.

Önce düşey düzlemden başlayalım. Eğik düzlemdeki cisim zıplamıyor, yani y ekseni doğrultusunda hareket etmiyor, öyleyse dengelenmiş kuvvetlerin etkisi altında, yani üzerindeki net kuvvet sıfır olmak zorunda.

-m\vec{g}cos \theta + \vec{N} = 0

Tepki kuvvetinin büyüklüğü mgcosθ, yönü de +y yönünde. (Eksi işareti -y yönünü gösteriyor.) Tepki kuvveti (normal kuvveti) daima yüzeye diktir, matematikte normal dik demektir.

\vec{N} = m\vec{g}cos \theta

Şimdi yatay bileşenlere bakalım. Ama önce sürtünme kuvvetini hesaplayalım. Tepki kuvvetini bildiğimiz için bu kolay olacak. k sürtünme katsayısını gösteriyor (statik sürtünme mi kinetik sürtünme mi sizce?):

\vec{f}_s = k|\vec{N}| \vec{f}_s = km|\vec{g}|cos \theta

Artık yataydaki net kuvveti hesaplayabiliriz. (Eksi işareti -x yönünü gösteriyor.)

\vec{F}_{net} = m\vec{g}sin \theta - \vec{f}_s

Dikkat etmemiz gereken sürtünme kuvvetinin yönünün daima harekete zıt yönde olduğu. Bu takozun eğik düzlemde hareket ettiğini varsayıyoruz, yani sürtünme kuvveti mgsinθ ‘dan daha küçük. Net kuvvetin büyüklüğü dolayısıyla şöyle olur:

|\vec{F}_{net}| = m|\vec{g}|sin \theta - |\vec{f}_s|

Artık, ivmenin büyüklüğünü de Newton’un ikinci hareket yasasını yazarak bulabiliriz.

\vec{F}_{net} = m\vec{a} a = \frac{mgsin \theta - kmgcos \theta}{m}

Sadeleştirirsek:

a = \frac{\cancel{m}g (sin \theta - kcos \theta)}{\cancel{m}} a = g(sin \theta - kcos \theta)

Dışarıdan bir kuvvet etkimediği zaman, eğik düzlemde hareket eden bir cismin ivmesinin kütlesinden bağımsız olduğu sonucuna ulaştık. Bu ne anlama gelir? 100 kg’lik bir cismin de 10000 kg’lik bir cismin de eğik düzlemde ivmesi aynıdır.

Sürtünmesiz eğik düzlem

Eğik düzlemi incelerken en genel durumu ele aldık ve sürtünme kuvvetinin bulunacağını düşündük. Peki sürtünme kuvveti yoksa (yani ihmal edebileceğimiz, yok sayabileceğimiz kadar küçükse, önemsizse)? O zaman cismin hareketi nasıl olur? Tek yapmamız gereken serbest cisim diyagramındaki sürtünme kuvvetini silmek. O zaman Newton’un ikinci yasasını şöyle yazabiliriz:

\vec{F}_{net} = m\vec{a} \vec{F}_{net} = m\vec{g}sin \theta \cancel{m} \vec{a} = \cancel{m}\vec{g}sin \theta \vec{a} = \vec{g}sin \theta

Yine, dışarıdan bir kuvvet etkimediği zaman, eğik düzlemde hareket eden cismin ivmesi kütlesinden bağımsız çıktı.

Eğik düzlem kullanarak statik ve kinetik sürtünme katsayısının ölçülmesi

Eğik düzlem kullanılarak sürtünmeli bir yüzeyle bir cisim arasındaki statik sürtünme katsayısını bulabilir miyiz? Evet 🙂 Ama nasıl? Cismi eğik düzlemin üzerine yerleştiririz sonra eğik düzlemin açısını yavaş yavaş artırırız.

Örneğin yukarıdaki resimde bir kitabı böyle bir eğik düzlem üzerine yerleştirmişler ve açının da 4° olduğunu görüyoruz. Kitap hareket etmiyor. (Akıllı telefonla açı ölçme fikri harika değil mi?)

Sonra açıyı artırıyorlar. Aşağıdaki gibi 10° olduğu zaman kitap hala hareket etmiyor.

Nihayet açıyı daha da artırıp 15° yaptıklarında kitap kaymaya başlıyor (öteleme hareketi yapıyor).

15° cismin kaymaya başladığı açı olduğuna göre, bu an statik sürtünme kuvvetinin cismin ağırlığının eğik düzleme paralel olan bileşenine eşit olduğu duruma denk geliyor. Aşağıdaki resim kitabın tam bu andaki serbest cisim diyagramı.

Newton’un birinci kanununa göre kuvvetlerin eşitliğinden:

m\vec{g}sin \theta - \vec{f}_{s-statik} = 0 \vec{N}-m\vec{g}cos\theta = 0 k_{statik}.|\vec{N}| = m\vec{g}sin \theta k_{statik}.m|\vec{g}|cos \theta = m\vec{g}sin \theta

Eşitliğin iki tarafını da mg’ye bölersek ve sadece kuvvetlerin büyüklüklerini alırsak:

k_{statik} = \frac{sin \theta}{cos \theta} = tan \theta

Bu kitap için statik sürtünme kuvvetinin en büyük değerini hesaplayabiliriz:

\theta = 15 ^\circ k_{statik} = tan 15^\circ = 0,268

Bu bulduğumuz en yüksek (azami veya maksimum) statik sürtünme katsayısı. Cisim harekete geçtikten sonra azalacak, çünkü kinetik sürtünme katsayısı statik sürtünme katsayısının en büyük değerinden küçüktür.

Eğer kitap eğik düzlemde sabit hızla giderse, o zaman kinetik sürtünme katsayısını da hesaplayabiliriz. Hareket denklemimiz tam olarak statik sürtünmeyle aynı olacak yalnızca açı değişecek.

k_{kinetik} = \frac{sin \theta}{cos \beta} = tan \beta k_{kinetik} < k_{statik} ; \beta < \theta

Flipping Physics’in bu videosunu izleyebilirsiniz.

Eğik düzlem örnek soru:

Bir eğik düzlem düzeneğine yerleştirilen bir takoz eğik düzlemin yatayla açısı 45° olunca sabit hızla hareket ediyor. Eğik düzlemin açısı 60°’ye çıkarılırsa takozun ivmesinin büyüklüğü kaç m/s² olur? (sin 45° = cos 45° = √2/2; sin 60° = √3/2 ;cos 60° = 1/2, g = 10 m/s²).

Çözüm:

Serbest cisim diyagramını siz çizin. Sonra işlemleri takip edersiniz.

Cisim sabit hızla hareket ederken sürtünme kuvveti ağırlığın eğik düzleme paralel olan bileşenine eşit. Sabit hızla hareket ettiği için net kuvvet sıfır olmak zorunda çünkü.

\vec{F}_{net} = m\vec{g}sin \theta - \vec {f}_{s} = 0 k_{kinetik}.m|\vec{g}|cos \theta = m\vec{g}sin \theta k_{k} = tan \theta k_{k} = tan 45^\circ = 1

Kinetik sürtünme katsayısını bulduk. Şimdi 60° için hareket denklemini yazalım. Düşeyde hareket yok, sadece yataya bakıyoruz.

\vec{F}_{net} = m\vec{a} \vec{F}_{net} = m\vec{g}sin \theta - \vec{f}_s

Sürtünme kuvvetinin yönü harekete zıt:

\vec{F}_{net} = m\vec{g}sin 60^\circ - k_{k}m|\vec{g}|cos 60^\circ \cancel{m}\vec{g}(sin 60^\circ - cos 60^\circ) = \cancel{m}\vec{a} |\vec{a}| = 10 (\frac{\sqrt{3}}{2}-\frac{1}{2}) \space m/s^2 |\vec{a}| = 5 (\sqrt{3} - 1) \space m/s^2 |\vec{a}| = 5 (1,73 - 1) \space m/s^2 |\vec{a}| = 5 (0,73) \space m/s^2 |\vec{a}| = 3,66 \space m/s^2

√3 irrasyonel bir sayı (iki tam sayının oranı olarak yazılamıyor, virgülden sonra birbirini tekrar etmeyen şekilde sonsuza kadar uzuyor tıpkı π gibi) ama ilk iki basamağını alıp yaklaşık bir sonuç bulabiliyoruz.

Dinamik ile ilgili mutlaka okumanız gereken yazılar

1. Dinamik nedir? Sürtünmesiz düzlemde sorular ve çözümler
2. Dinamik soruları ve çözümleri
3. Atwood makinesi nedir? Birbirine bağlı cisimler soruları
4. Eylemsizlik kuvveti nedir? Asansör soruları

Eğik düzlem ile ilgili kazanımlar

2017 – 11.1.3.1. Net kuvvetin yönünü belirleyerek büyüklüğünü hesaplar.

• Serbest cisim diyagramları üzerinde cisme etki eden kuvvetlerin gösterilmesi sağlanır.
• Yatay, düşey ve eğik düzlemde sürtünme kuvvetinin yönü belirlenerek büyüklüğünün hesaplanması sağlanır.

2017 – 11.1.3.2. Net kuvvet etkisindeki cismin hareketi ile ilgili hesaplamalar yapar.

• Hesaplamaların günlük hayat örnekleri üzerinden yapılmasına özen gösterilir.
• Sürtünmeli ve sürtünmesiz yüzeyler dikkate alınmalıdır.