Snell Yasası nedir? Kırılma Kanunları

Bir ortamdan başka bir ortama geçen ışığın kırıldığını öğrendik. Şimdi kırılmanın nelere (yani hangi değişkenlere) bağlı olduğunu inceleyeceğiz. Bu değişkenler arasındaki ilişkileri açıklayan kırılma kanunları nelermiş göreceğiz, özellikle de Snell yasası üzerinde duracağız.

Snell Yasası nedir?

Snell yasası ortam değiştiren ışığın geldiği ortamın kırılma indisi ve gelme açısı ile girdiği ortamın kırılma indisi ve kırılma açısı arasındaki matematiksel ilişkidir. Ne demek bu? Bükülen Işık PHET Simülasyonunu kullanıp, veri toplayarak, sonra da topladığımız veriyi analiz ederek görelim. Önce fiziksel olayı gösterelim ve hangi değişkenlerle ilgilendiğimizi belirleyelim.

Aşağıdaki resimde sol üst köşede bir lazer var. Lazerin bulunduğu ekranın üst yarısı hava (yani birinci ortam ya da ışığın geldiği ortam.) Ekranın alt yarısı su (yani ikinci ortam.) Ayrıca havanın ve suyun kırılma indislerini de biliyoruz. n_hava = 1 ve n_su = 1,33. Bir de, ışığın tam ortam değiştirdiği noktaya, gelme açısını ve kırılma açısını ölçebilmek için bir açı ölçer yerleştirilmiş. Havayla suyun birleştiği yüzeye dik çizilen ve kesikli çizgiyle de normal doğrusunun gösterildiğini görüyoruz.

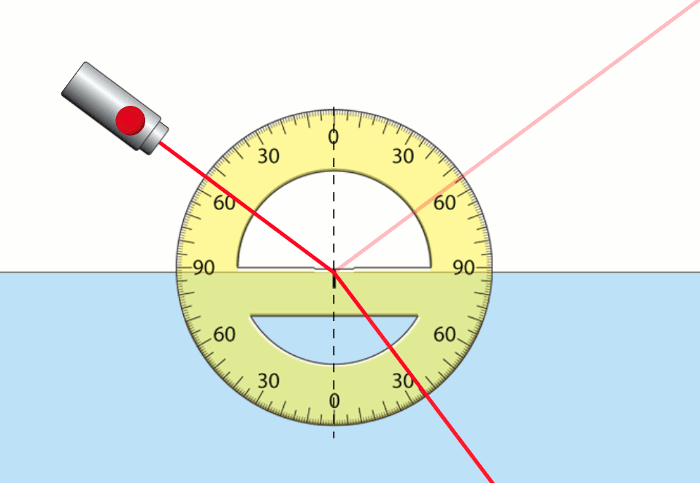
Bu resimde lazerden gelen ışığın gelme açısının (normalle yaptığı açının) 55° olduğunu, kırılma açısının (bu da kırılan ışığın normalle yaptığı açı) 35° olduğunu görüyoruz. Ayrıca suyun yüzeyine ulaşan ışığın sadece kırılmadığını ayrıca yansıdığını da görüyoruz. Işığın düzgün yansıma yaptığını da yansıma açısının (yine yansıyan ışının normalle yaptığı açı) 55° olmasından bu sonuca varıyoruz.

Şimdi sistemli olarak gelme açısını değiştirip, kırılma açısının nasıl değiştiğini ölçelim ve ölçümlerimizi kaydedelim. Aşağıdaki tabloda benim topladığım veri görülüyor.

Gelme açısı	Kırılma açısı
10	6
20	15
30	21
40	27
50	33
60	39
70	43
80	46

Verimiz sayı çifti olduğuna göre bir dağılım grafiği çizip bakalım bir ilişki var mı bu sayılar arasında? Önce bir dağılım grafiği çizip eğilim eğrisi ekliyorum grafiğe. Şöyle görünüyor:

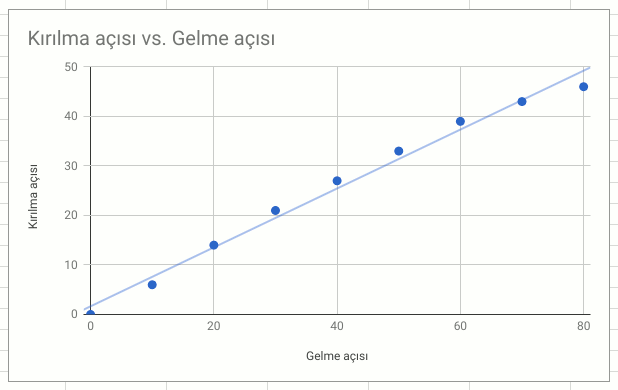
Eğilim çizgisi gelme açısıyla kırılma açısı arasında doğrusal (y = mx +b şeklinde) bir ilişki olabileceğini gösteriyor, ama noktalar bu çizginin üstünde dizilmemiş. Açılarla uğraştığımda trigonometrik dönüşümler yaparak başka ilişkiler arayabileceğimi biliyorum (artık siz de biliyorsunuz.) Öyleyse ilk aklıma gelen dönüşüm olan sinüs dönüşümünü deneyeyim. Yani gelme açısının sinüsünü (sin i diyelim buna) ve kırılma açısının sinüsünü (sin r diyelim buna da) alıp, grafiği bir de öyle çizelim. Bu kez şöyle görünüyor:

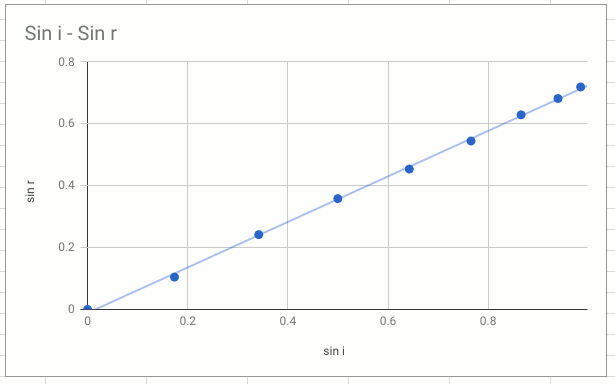
Bu ilk grafiğe göre çok daha iyi. Noktaların çoğunun çizgiye çok yakın olduğunu, bazılarının da ip gibi eğilim çizgisinin üztünde dizildiğini görüyoruz. Bu grafiği kullanmak ilkine göre daha mantıklı dolayısıyla. Şimdi de eğilim çizgisinin eğimini bulalım. Bunun için tablodaki üçüncü noktayı seçebilirim.

\frac{sin(i)}{sin(r)} = \frac{sin(20^\circ)}{sin(15^\circ)} = \frac{0,341}{0,258} = 1,32

Bu ilginç bir sonuç, çünkü suyun kırılma indisine çok yakın (n_su = 1,33). Eğer bu deneyi başka malzemelerle yapacak olsaydık, şöyle bir genellemeye ulaşırdık:

\frac{sin(i)}{sin(r)} = \frac{n_{su}}{n_{hava}}

İşte bu ilişkiye Snell yasası deniyor. En genel haliyle formülü yazarsak:

\frac{sin(i)}{sin(r)} = \frac{n_{2}}{n_{1}}

Düzenlersek:

n_1sin(i) = n_2sin(r)

Snell yasasını bir de kelimelerle ifade edelim: Işığın geldiği ortamın kırılma indisinin gelme açısının sinüsüyle çarpımı, ışığın kırıldığı ortamın kırılma indisiyle kırılma açısının çarpımına eşittir.

Müfredat matematiksel işlemlere girilmez diyor, öyleyse nitel olarak Snell yasasının anlamını gözden geçirelim:

• Kırılma indisi düşük (optik olarak yoğun) ortamdan kırılma indisi yüksek (optik olarak daha az yoğun) olan ortama gelen ışın kırılırken normale yaklaşır. Bunu bu sayfadaki ilk resimde görebiliyoruz. Kırılma açısı gelme açısından daha küçük oluyor. Optik olarak yoğunluk kavramı daha önce öğrendiğiniz yoğunluk veya özkütle kavramından tamamen farklı bir kavram. Özkütle ile kırılmanın bir ilişkisi yok.
• Kırılma indisi yüksek ortamdan kırılma indisi düşük olan ortama gelen ışın kırılırken normalden uzaklaşır. Yani kırılma açısı gelme açısından daha büyük oluyor. Bunu da aşağıdaki resimde görüyoruz.

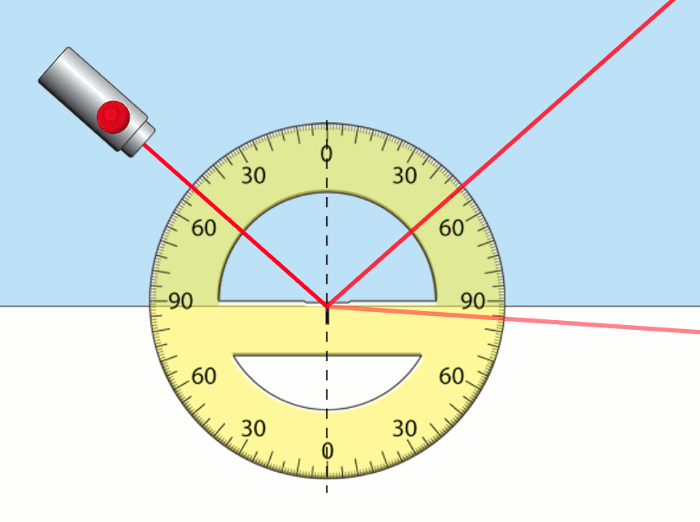
Bu resimde resmin üst yarısı su, alt yarısı hava. Sudan gönderilen ışık gelme açısı 50° olacak şekilde su-hava yüzeyine ulaşıyor, kırılma açısının da 84° olduğunu görüyoruz. Bu çok dramatik bir değişim. Daha sonraki yazımızda sınır açısı ve tam iç yansımayı incelerken, gönderilen ışığın hiç kırılmadığı durumlar olduğunu da göreceğiz. Ayrıca prizmalar ve mercekler Snell yasasına göre tasarlanan optik aletlerdir.

Son olarak ışığın taşıdığı enerjinin ölçüsü olan ışık şiddetinin kırılma olayı esnasında değiştiğini de hatırlatmalıyım. Enerjinin korunumu yasasına göre, gelen ışığın enerjisi kırılan ve yansıyan ışığın enerjilerinin toplamına eşit olmak zorunda.

Fermat Prensibi

Snell yasası ışığın nasıl kırıldığını açıklıyor, ama neden öyle kırıldığını açıklamıyor. Bunu Fransız matematikçi Pierre de Fermat açıklamış. Matematiksel çıkarımı çok zarif olmasına rağmen, türevi öğrenmeden anlayamayacağınız için nitel olarak açıklayayım. Bunun için boğulan adam ve can kurtaran benzetmesini (analojisini) kullanacağız.

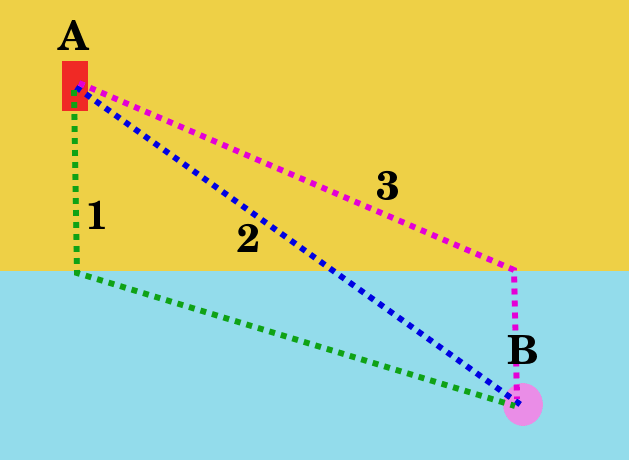
Yukarıdaki resim bir plajı temsil ediyor. Sarı bölge kum, mavi bölge deniz. A noktasında can kurtaran var, denize bakınca B noktasında bir kişinin yardım istediğini görüyor. Sorumuz şu: Can kurtarının boğulan kişiye en hızlı ulaşması için hangi yolu seçmesi gerekir? Hızlı ulaşmasının önemli olduğu açık, ne kadar hızlı ulaşırsa kişiyi boğulmaktan kurtarma ihtimali o kadar yükseliyor.

Yeşil çizgi ile gösterilen 1 numaralı yolu seçerse kumdan denize dik olarak koşup, sonra denizde doğrudan adama doğru yüzebilir. Mavi çizgi ile gösterilen 2 numaralı yolu, ki bu A ve B noktaları arasındaki en kısa yol yani bir doğru, seçebilir. Mor çizgiyle gösterilen 3 numaralı yolu seçip, kumda olabildiğince uzun süre koşup, kum ile adam arasındaki en yakın mesafeden yüzmeye başlayabilir. Can kurtaranın kumda koşma hızının denizde yüzme hızından daha yüksek olduğunu da belirtelim. Sizce can kurtaranın bu kişiye en kısa sürede ulaşması için hangi yolu seçmesi gerekir?

1 numaralı yolu seçerse kısa bir süre kumda koşup uzun bir süre yüzmesi gerekecek, bu en uzun süren yol olur. 2 numaralı yolu, yani en kısa yolu, seçerse kumdaki mesafe ve denizdeki mesafe eşit, ama daha yavaş yüzdüğünü düşünürseniz denizde kumda olduğundan daha uzun süre geçirecek. 3 numaralı yolu seçerse yolu 2 numaralı yola göre uzatmış olacak, ama kumda denizde olduğundan daha hızlı ilerleyecek ve denizde daha az mesafe kalacak. Dolayısıyla en kısa süren yol 3 numaralı yol olur, bunun en kısa mesafe olmadığına dikkat edin.

İşte Fermat’ın fikri de bu benzetime dayanıyor. Işık daima en kısa süreyi alacağı yolu izliyor, en kısa mesafeyi değil. Bu nedenle ortam değiştirirken kırılıyor. Snell yasası da Fermat’ın en kısa süre ilkesinden türemiş oluyor.

Snell yasası ve kırılma kanunları ile ilgili kazanımlar

2017 – 10.4.6.1. Işığın kırılmasını, su dalgalarında kırılma olayı ile ilişkilendirir.

• Deney veya simülasyonlar kullanılarak ortam değiştiren ışığın ilerleme doğrultusundan sapma miktarının bağlı olduğu değişkenleri belirlemeleri sağlanır. Snell Yasası’nın matematiksel modeli verilir.
• Snell Yasası ile ilgili matematiksel hesaplamalara girilmez.
• Snell Yasası ile ilgili matematiksel hesaplamalar yapılması sağlanır. (Fen lisesi)