Volta 1800 yılında pili icat ettikten sonra bilim insanları elektrikle neler yapabileceklerini görmek için bu konuya üşüştüler. Bu bilim insanlarından biri Danimarkalı Hans Christian Oersted’di. Aslında niyeti elektrikle manyetizma arasında bir ilişki var mı diye araştırmak değildi. Elektrik devreleriyle ilgili başka bir deney yaparken devrenin tellerinin birinin yakınında bir pusula unutmuştu. Devreyi çalıştırıp tellerden elektrik akımı geçmesini sağladığında gözü pusulaya kaydı ve pusulanın iğnesinin yönünün saptığını fark etti. Bu tatlı kaza elektrikle manyetizma arasında bir ilişkinin olduğunu gösterdi. Bilim insanlarına üşüşecek yeni bir konu daha çıkmıştı. Elektrik manyetizmayı, manyetizma elektriği nasıl etkiliyor sorusunu sistemli olarak araştırmaya başladılar. Akım şiddeti arttıkça pusula daha fazla sapıyor muydu? Pusulayı telden uzaklaştırınca sapma miktarı değişiyor muydu?
Akım geçen telle pusulaların ne ilgisi olabilir? Önce olayın kendisini görmeliyiz. Pusulanın manyetik alanın var olup olmadığını ve varsa yönünü belirlemek için bir algıç (sensör) gibi kullanıldığını öğrenmiştiniz. Pusulalar, bulundukları noktadaki manyetik alan vektörünün yönünü gösteriyor. Örneğin, düz bir karton alsak üstüne bir sürü pusula yerleştirsek sonra üstü pusula dolu bu kartonu bir masaya koysak pusulaların nasıl davranmasını bekleriz? Etrafta mıknatıs gibi manyetik alan yaratan bir cisim yoksa tüm pusulalar aynı yönü göstermez mi? Yani kuzeyi. (Dünya’nın manyetik alanını bir hatırlamak isteyebilirsiniz.) Aşağıdaki fotoğrafta tam da bunu görüyoruz. Fotoğrafta kartonun ortasından düz bir bakır tel geçiyor ama telin üstünden akım geçmiyor.

Kartonun ortasındaki teli bir pile bağlasak yani telin üstünden akım geçmesini sağlasak pusulalar nasıl davranır? Bir düzenlilik, bir örüntü görür müyüz? Aşağıdaki fotoğrafta telin üstteki ucu pilin artı kutbuna alttaki ucu eksi kutbuna bağlanmış. Yani telin üzerinden akım yukarıdan aşağıya doğru geçiyor.

Bu fotoğrafı birlikte inceleyelim. Pusulaların kuzeyi gösteren sivri uçlarının telin etrafında bir çember oluşturduğunu fark edebildiniz mi? Manyetik alan akım geçerken düz telin etrafında bir çember etrafında dolanıyor. Telin pille bağlantısını kesip akımı durdurursak pusulalar ilk fotoğraftaki hallerine dönüyorlar, hepsi yine kuzeyi gösteriyor.
Şimdi de telden geçen akımın yönünü değiştirmeyi deneyelim. Bütün yapmamız gereken telin altta kalan ucunu pilin artı kutbuna üstte kalan ucunu da pilin eksi kutbuna bağlamak. Böylece akım telden ilk durumun tam tersi yönde, yukarı doğru geçecek. Aşağıdaki fotoğrafta bu durum gösteriliyor.

Pusulaların iğnelerinin yine bir çember şeklinde telin etrafını sardığını görüyoruz. Ama ilk duruma göre bir fark var. İki fotoğrafa dikkatli bakın ve karşılaştırın. İkinci fotoğrafta pusula iğnelerinin sivri uçları ilk fotoğraftaki durumun tam zıttı yöndeler. Pusula iğneleri telin etrafını yine sarıyor ama ilk duruma göre zıt yönde sarıyor.
Sağ el kuralı ile manyetik alanın yönü nasıl bulunur?
Akım ve manyetik alanın ilişkisini daha önce biraz incelemiştik şimdi daha derine ineceğiz. Buraya kadar gözlemlediğimiz iki durum hakkında fikir yürütelim. Acaba telden geçen akımın yönüyle oluşan manyetik alanın bir ilişkisi var mı? Akımın yönünü bilirsek pusulaların çemberde hangi yönde döneceğini bilebilir miyiz? Bu ilişkiyi bulmanın bir yolu olabilir mi?
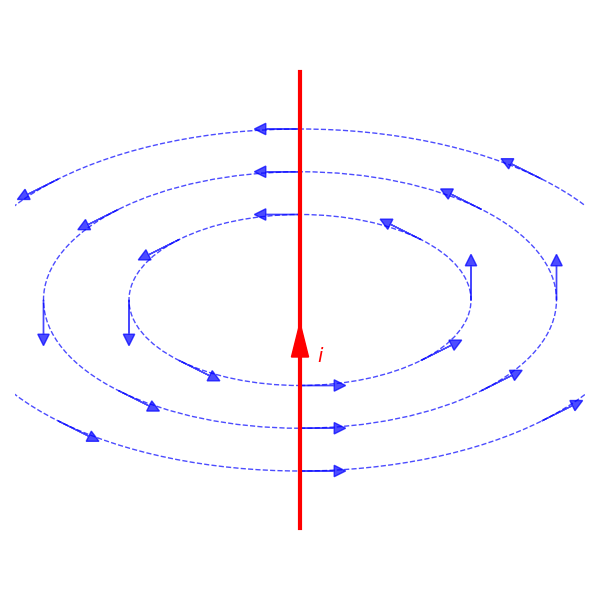
Üç sorunun da cevabı evet. Pusulaların sivri uçlarının gösterdiği manyetik alanın dolanım yönünü bulmanın bir yolu sağ el kuralını kullanmak. Manyetik dolanımın yönünü bulmak için sağ elinizin başparmağını akımın yönünü gösterecek yönde tutuyorsunuz. Sonra diğer parmaklarınızı avuç içinize doğru kıvırıyorsunuz. Parmaklarınızın döndüğü yön manyetik dolanımın yönü oluyor. Aşağıdaki resimde sağ el kuralının manyetik alanın dolanımı için nasıl kullanıldığını görebilirsiniz. Başparmağın üstündeki siyah C vektörü akımın yönünü (yukarı doğru), diğer parmakların kıvrıldığı kırmızı oklar manyetik dolanımın yönünü gösteriyor. Elinize tam tepeden bakıyor olsaydınız akımın başparmağınızın ucundan size doğru geldiğini manyetik alanın da saat yönünün tersinde dolandığını görürdünüz. Kendiniz bir deneseniz çok iyi olur. Yanlışlıkla sol elinizi kullanmadığınıza dikkat etmelisiniz.

Şimdi de akımın yukarıdan aşağıya doğru olduğu durumda sağ el kuralını kullanalım. Sağ elimizin başparmağı aşağıyı gösteriyor. Parmaklarınızı avuç içinize doğru sardığınızda saat yönünde döndüğünü görmüş olmalısınız. Aşağıdaki resimde bu durum gösteriliyor. Manyetik dolanımın ilk durumun tam zıttı yönde olduğunu, akım yukarı yönlü geçerken saat yönünün tersinde, akım aşağı geçerken saat yönünde dolandığını fark etmiş olmalısınız.
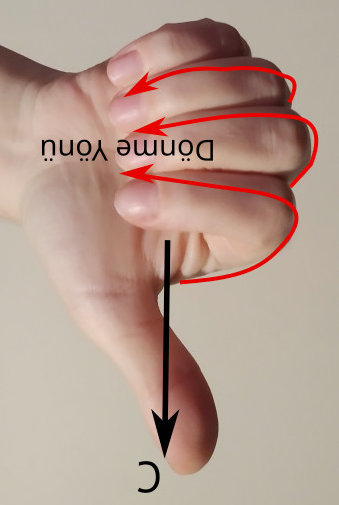
Aşağıdaki resimde akım geçen düz telin (kırmızı çizgi) etrafında seçtiğimiz bir çemberin (elips gibi görünüyor) üstündeki manyetik dolanımı görüyoruz. Akım telde aşağıdan yukarı gidiyor, çemberin üstünde altı nokta seçmişiz bu noktalardaki manyetik alan vektörleri de mavi oklarla gösteriliyor.
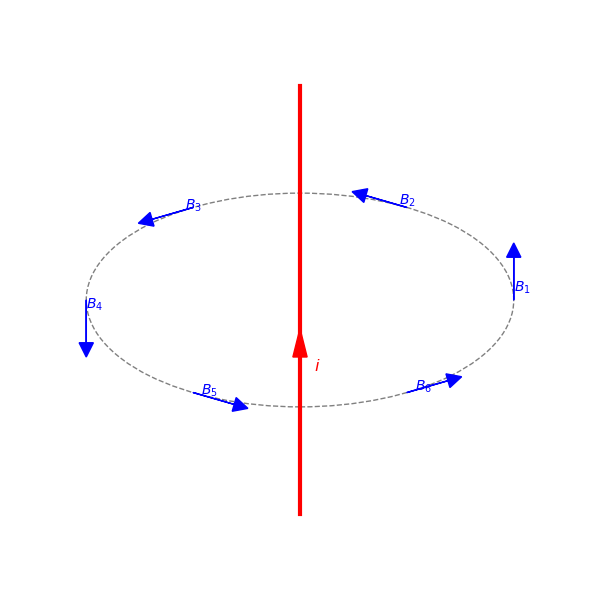
Ama telin etrafındaki uzayın her yerinde manyetik alan oluşuyor. Bunu göstermek için manyetik alan çizgilerini ve bir kaç çemberi daha kullanabiliriz. Aşağıdaki resimde üç çember üstünde manyetik alanın nasıl dolandığı gösteriliyor. Çemberler telden uzaklaştıkça manyetik alan vektörlerinin boyunun kısaldığını fark ettiniz mi? Ayrıca manyetik alan çizgilerinin bu çemberlerde bir başlangıç ve bir bitiş noktasının olmadığını fark ettiniz mi? Bir soru daha. Aslında ilk iki çemberin arasında kaç çember daha var? Cevaplarınızı yorumlarda bekliyorum.
Akım ve manyetik alanın iki boyutta gösterimi
Fotoğraflarda ve resimlerde gerçekte üç boyutlu olan şeyleri iki boyutta görüyoruz, kağıdın veya ekranın yüzeyinde. Perspektif algımızdan dolayı üç boyutlu cisimleri iki boyutta temsil edebiliyoruz. Bir üstteki resimde manyetik alanın dolanımını yaparken aslında çember olan bir şekli elips olarak gösterdim örneğin. Akım ve manyetizma işin içine girince işimizi kolaylaştırmak için üç boyutu iki boyuta indirgemenin kolay bir yolu olsa harika olmaz mı? Çok sık kullandığımız bir yöntemi birlikte görelim.
Aşağıdaki fotoğrafta düz bir kağıdı delip geçen bir kurşun kalemi görüyoruz. Kalemin sivri ucu bize bakıyor. Bu tıpkı bir okun sayfadan (veya ekrandan) bize doğru gelmesine benziyor. Bu kalem bir iletken teli temsil ediyor, sivri uç da akımın yönünü. Sağ el kuralını kullanarak manyetik alanın yönünün saat yönünün tersinde olduğunu bulabiliyoruz.
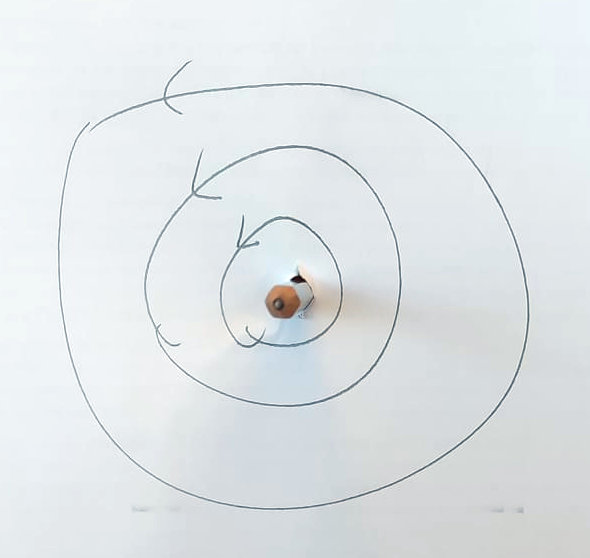
Aşağıdaki fotoğrafta da aynı kalemin bu kez arka ucu görünüyor. Kalemi akım geçen iletken bir tel olarak düşünürsek akım sayfadan (veya ekrandan) içeri doğru gidiyor. Bu kez manyetik alanın yönünün saat yönünde olduğunu görüyoruz. Sağ el kuralıyla kontrol etmenizi tavsiye ederim.
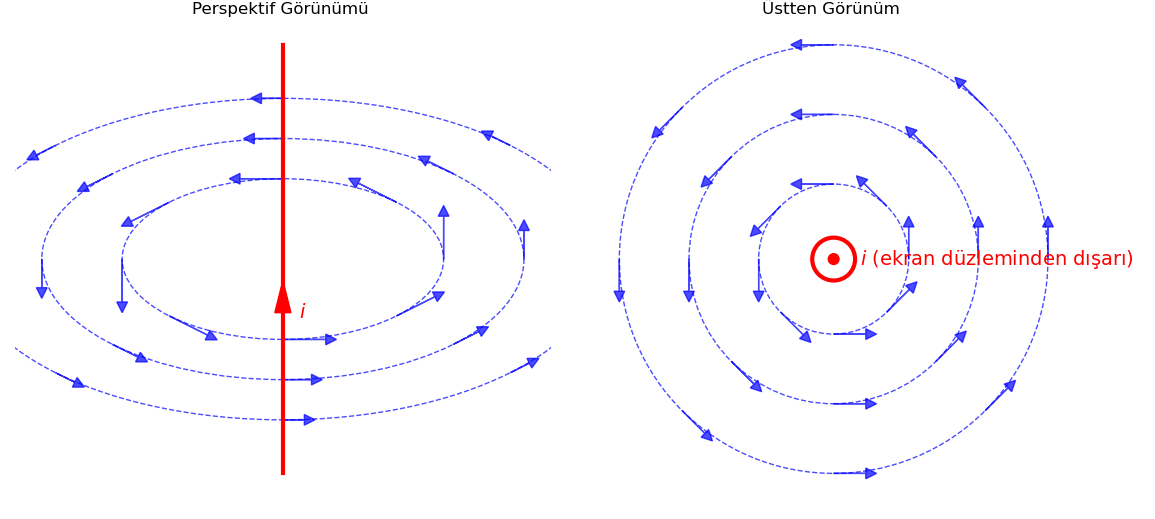
Şimdi de fotoğraf yerine basitleştirilmiş çizimler kullanarak üç boyuttaki vektörleri iki boyutta nasıl temsil ettiğimize bakalım. Aşağıdaki resimde akım geçen bir telin perspektif görünümü ve üstten görünümü gösteriliyor. Perspektif görünümünde akım aşağıdan yukarı doğru. Bu tele üstten bakınca akım bize doğru geliyor, yani sayfa (veya ekran) düzleminden dışarı doğru. Bunu küçük bir çemberin içine çizdiğimiz bir nokta ile gösteriyoruz. Üstten bakınca okun ucunu görüyoruz, bize doğru geliyor.
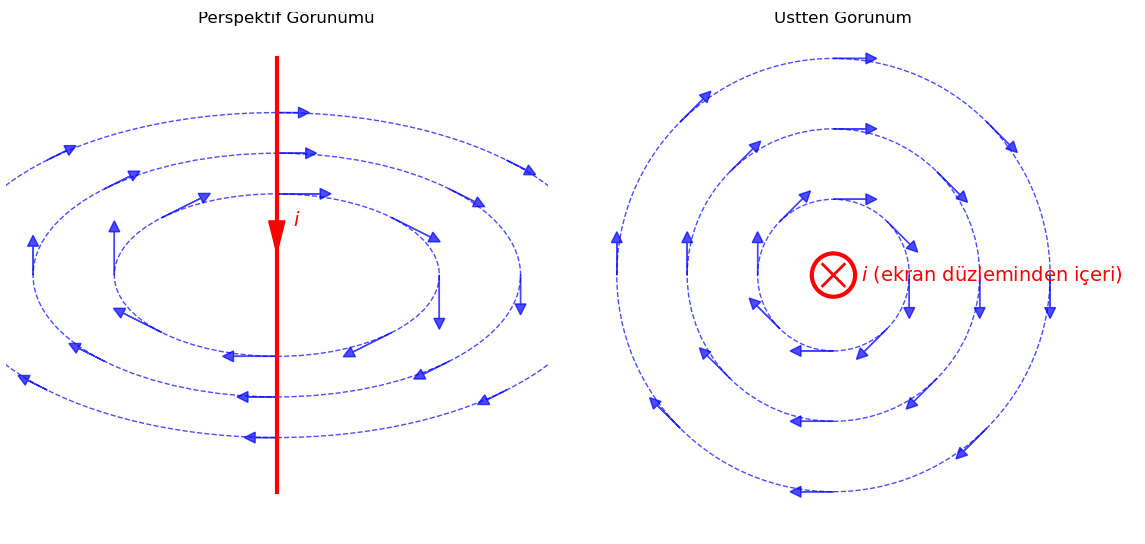
Aşağıdaki resim bir önceki resme benziyor, tek farkı bu kez akımın perspektif görünümünde yukarıdan aşağıya geçmesi. Bu durumda tele üstten bakınca akım sayfa (ekran) düzleminden içeri doğru. Akımın yönünü (sayfa düzleminde içeri doğru) temsil etmek için küçük bir çemberin içine çizilmiş bir çarpı işaretini kullanıyoruz. Üstten bakınca okun arkasını görüyoruz, bizden uzaklaşıyor.
Son olarak bu gösterimi sadece akımı temsil etmek için kullanmıyoruz. Üç boyuttaki tüm vektörleri temsil etmek için kullanabiliriz. Örneğin aşağıdaki resimde kırmızı çizgi akım geçen teli temsil ediyor, akım soldan sağa doğru. Bu durumda manyetik alan vektörü telin üst kısmında sayfadan dışarı doğru, telin alt kısmında sayfadan içeri doğru. Telin çevresinin manyetik alan vektörleriyle dolu olduğunu görebiliyor musunuz?

Akım geçen düz iletken telin çevresinde oluşan manyetik alanın büyüklüğü hangi değişkenlere bağlıdır?
Buraya kadarki incelemelerimiz niteldi. Şimdi nicel yani matematiksel incelememizle devam ediyoruz. Aslında Ampere kanununu kullanarak çok estetik bir şekilde türetebiliriz, ama lise seviyesinde cebirle yetinmek zorundayız. Manyetik alanın bağlı olduğu değişkenleri deneyden elde edilen sonuçlar olarak vereceğiz.
Akım şiddeti
Eğer düz bir telden akım geçirip etrafındaki manyetik alanın büyüklüğünü ölçseydiniz akım şiddeti arttıkça manyetik alanın büyüklüğünün de arttığını, yani bu iki değişkenin doğru orantılı olduğunu görürdünüz. Öyleyse:
|\vec{B}| \propto i
|\vec{B}| manyetik alanın büyüklüğünü i akım şiddetini gösteriyor.
Telden uzaklık
Aynı deneyde manyetik alan şiddetinin telden uzaklıkla ters orantılı olduğunu, yani telden uzaklaştıkça azaldığını görürdünüz. Öyleyse:
|\vec{B}| \propto \frac{1}{d}
|\vec{B}| manyetik alanın büyüklüğünü d telden uzaklığı gösteriyor.
Ortamın manyetik geçirgenliği
Elektriksel kuvveti öğrenirken Coulomb kanununda kuvvetin ortamın elektrik geçirgenliğiyle (\epsilon) ilgili olduğunu öğrenmiştiniz. Benzer şekilde manyetik alanın büyüklüğü de ortamın manyetik geçirgenliğiyle (\mu) doğru orantılı.
|\vec{B}| \propto \mu
Akım geçen düz telin manyetik alan şiddetinin matematiksel modeli (formülü)
Bu değişkenler arasındaki ilişkileri bir eşitlik olarak ifade edersek:
|\vec{B}| = \frac{\mu i}{2\pi d}
Eğer ortamı boşluk olarak alırsak o zaman boşluğun manyetik geçirgenliği katsayısını kullanabiliriz:
|\vec{B}| = \frac{\mu_0 i}{2\pi d}
Ders kitaplarınızda manyetik geçirgenlik yerine k diye bir başka katsayının kullanıldığını görebilirsiniz:
k = \frac{\mu_0}{4\pi}
Bu durumda manyetik alanın büyüklüğünü de şöyle ifade edebiliriz:
|\vec{B}| = \frac{2k i}{d}
İlgili Kazanımlar
2018 – 11.2.4.1 Üzerinden akım geçen iletken düz bir telin çevresinde, halkanın merkezinde ve bobinin merkez ekseninde oluşan manyetik alan şiddetini etkileyen değişkenleri analiz eder.