Elektriksel kuvvet ve Coulomb Yasası nedir? Nelere bağlıdır?

Elektrostatik konularını incelerken yüklü cisimlerin birbirini ittiklerini veya çektiklerini görmüştük, birbirlerine bir kuvvet uyguluyorlardı, bu kuvvete elektriksel kuvvet denir, birimi de (bu bir kuvvet olduğu için) Newton’dur (N). Elektriksel kuvvetin varlığını gördük, ama büyüklüğünü bilmiyoruz, tam olarak iki yüklü cisim birbirine ne kadar elektriksel kuvvet uygular? Bu sorunun cevabını Charles Augustine de Coulomb 1784 yılında keşfetmiş, bu nedenle elektriksel kuvvet onun adıyla anılır olmuş: Coulomb kuvveti denilmiş. İki elektrik yükü arasındaki etkileşimin matematiksel modeline (formülüne) de Coulomb yasası (kanunu, ilkesi veya prensibi) adı verilmiş. Columb yasasının keşfedildiği deney elektriksel kuvvetin niceliksel (sayısal) olarak hangi değişkenlere bağlı olduğunu anlamamızı kolaylaştırabilir.

Coulomb Deneyi: Coulumb Kuvveti nelere bağlıdır?

Coulomb burulma terazisi diye bir ölçüm aracı icat etmiş. Burulma terazisi, ucuna kuvvet uygulandığında dönen (açı yapan) bir araç, ne kadar kuvvet uygulandığını açı miktarını kıyaslayarak bulabiliyoruz. Columb’un yaptığı deneyin (ve burulma terazisinin) basitleştirilmiş hali şöyle:

Burulma terazisinin ucuna yük çeşidini ve miktarını bildiğimiz küçük bir yüklü cisim (iletken olması işleri kolaylaştırıyor) yerleştirelim. Sonra bir başka yük türünü ve miktarını bildiğimiz başka bir yüklü cismi, ilk cisme yaklaştıralım. Acaba elektriksel kuvvet nelere bağlı?

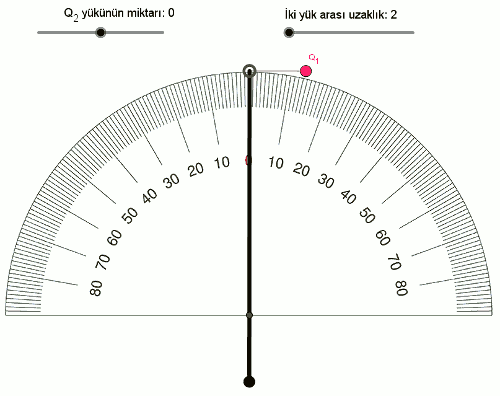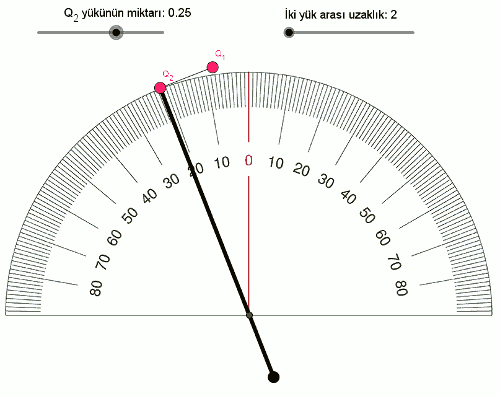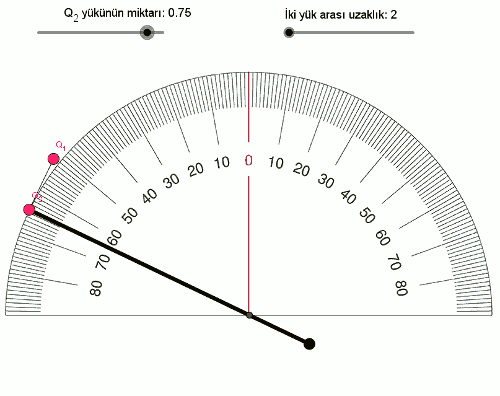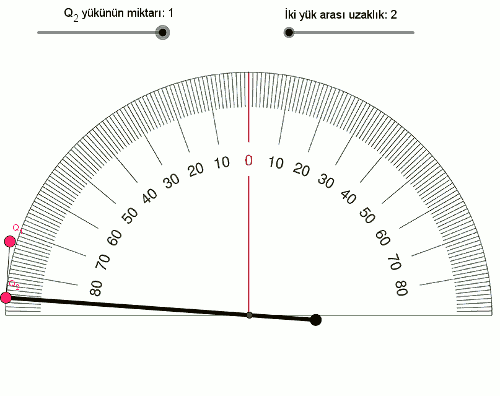
Başlangıçta şunu deniyoruz. İki cisimden biri yüksüz ise ne oluyor? Aşağıdaki resimde burulma terazisindeki cismin yüksüz (elektrik yükünün sıfır) olmasını sağladığımız zaman, iki cisim arasındaki etkileşimi görüyoruz. İki cisimden biri yüksüz olduğu zaman kuvvet uygulanmadığını fark etmiş olmalısınız. Öyleyse kuvvetle, iki yük arasındaki ilişki yüklerin toplamı ya da farkı olamaz, sadece çarpımı olabilir (bunu iyice bir düşünün neden?)

Aşağıdaki resimde ise Q₁ ve Q₂ yüklerinin miktarları ve cinsleri aynı, ikisi de pozitif (artı) yüklü. Kontrollü deney yapmak istediğimiz için sadece ilgilendiğimiz bağımsız değişkeni (yük miktarını) değiştireceğiz ve bunun sonucunda değişen bağımlı değişkeni (elektriksel kuvveti) ölçeceğiz. Elektriksel kuvveti ölçmek için burulma terazisinde elektriksel kuvvetin büyüklüğünün göstergesi olan açının büyüklüğünü ölçeceğiz. Bunun dışındaki tüm değişkenleri sabit tutmalıyız, en göze çarpan değişken iki yük arasındaki mesafe. Öyleyse, aradaki mesafeyi sabit tutalım; Q₂‘nin yük miktarıyla elektriksel kuvvetin ilişkisi nasılmış araştıralım.

Şimdi de neler bulduk sıralayalım: (Q₁ = 1 olduğunu bildiğimizi farz edelim.)

1. Q₂ = 0 olduğunda, açının değişmediğini (0° de kaldığını) dolayısıyla iki cismin etkileşmediğini yani birbirlerine elektriksel kuvvet uygulamadıklarını görüyoruz. Q₁Q₂ = 0
2. Q₂ = 0,25 (Q₁Q₂ = 0,25) olduğunda açı 22° oluyor.
3. Q₂ = 0,5 (Q₁Q₂ = 0,5) olduğunda açı 43° oluyor.
4. Q₂ = 0,75 (Q₁Q₂ = 0,75) olduğunda açı 64° oluyor.
5. Q₂ = 1 (Q₁Q₂ = 1) olduğunda açı 86° oluyor.

Elimizde iki sayı olduğuna göre (matematikte buna sıralı ikili diyoruz), bu sayılar (Q₁Q₂, açı) arasındaki ilişkiyi araştırmak için grafik çizmek. Aşağıdaki grafikte x -ekseni yüklerin büyüklüklerinin çarpımını, y- ekseni açıyı gösteriyor.

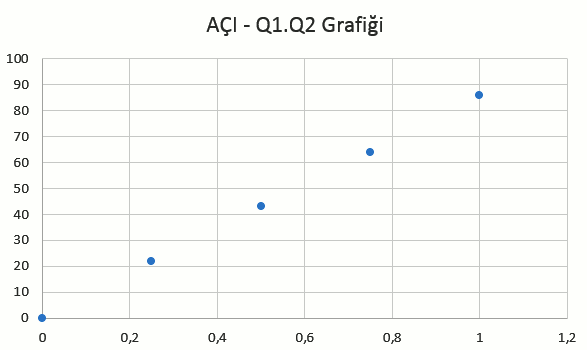
Bu grafiğin doğrusal olduğu çok muhtemel. Yani noktaları birleştiren bir doğru çizebiliriz (buna matematiksel model diyeceğiz, grafiğe eğilim çizgisi ekleyeceğiz). Aşağıdaki resim de bu grafiğe oturtulmuş doğruyu gösteriyor. (Bunu excel ile kolayca yapabiliyoruz.)

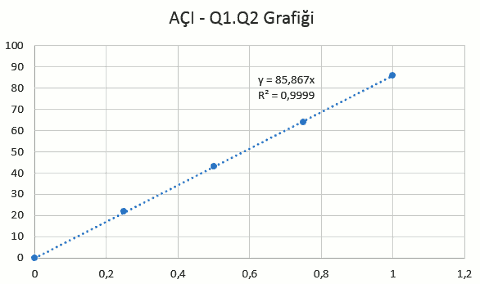
Grafikteki doğrunun eğimi (85,867 değeri) yüklerin büyüklüğünün çarpımıyla açı (kuvvet) arasındaki ilişkinin oranını gösteriyor. R² = 0,9999 değeri ise bu noktalara bu doğrunun ne kadar iyi oturduğunun göstergesi. 1’e yakın değerler iyi oturmuş demek, bu model (doğru) bu veriye gerçekten çok iyi oturmuş. Buradan varacağımız sonuç şöyle:

Açı yük miktarlarının çarpımıyla doğru orantılı. Demek ki elektriksel kuvvet de yüklerin büyüklüklerinin çarpımıyla doğru orantılı.

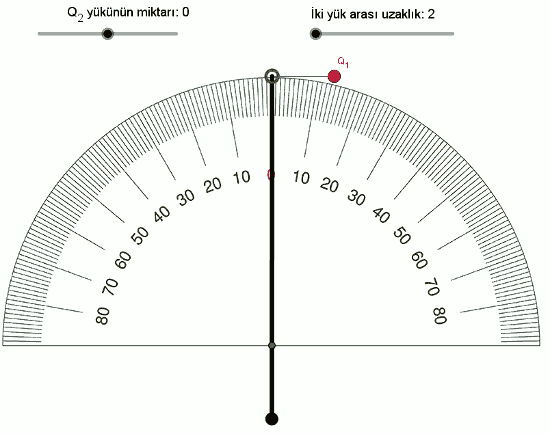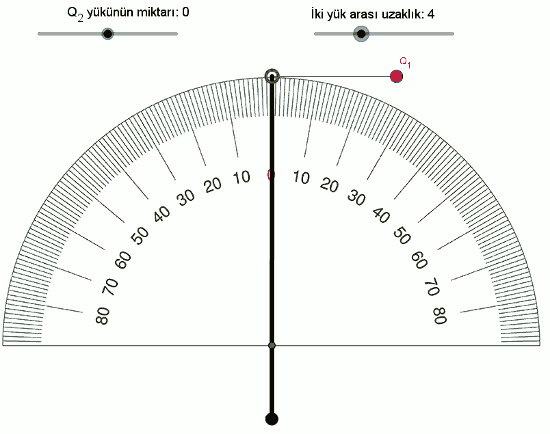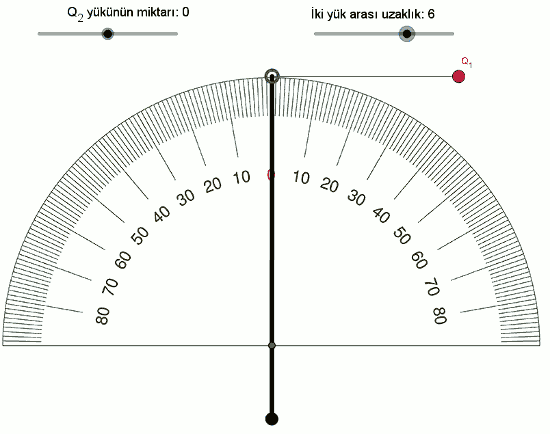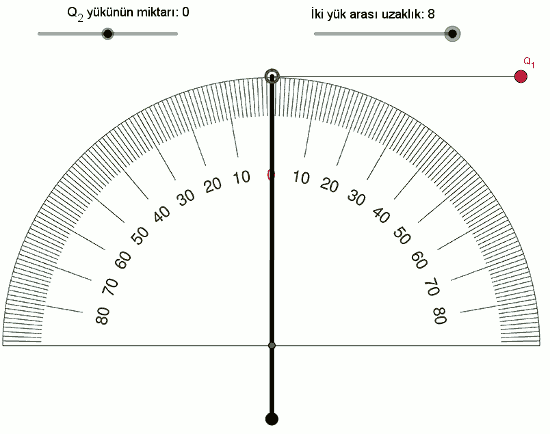
F \space \alpha \space Q_1 \times Q_2

Şimdi de yükleri sabit tutup, yüklerin arasındaki mesafeyle (uzaklıkla) elektriksel kuvvetin ilişkisini inceleyelim. İki yükün arasındaki mesafeyi 2’den başlayarak 0,25 adımlarla artıralım, şöyle görünüyor:

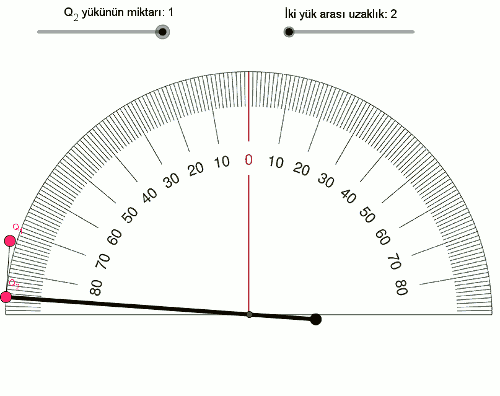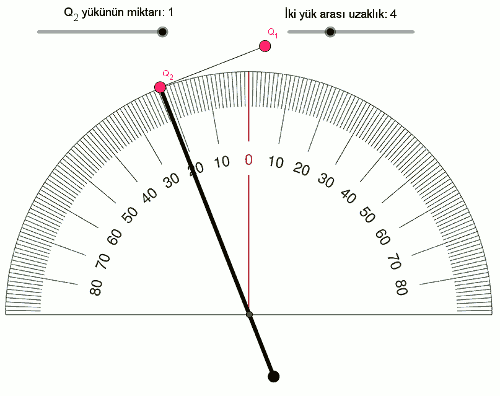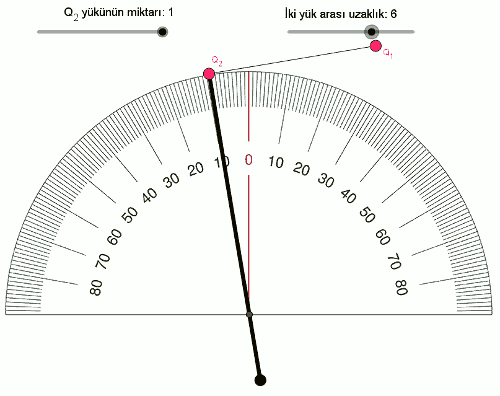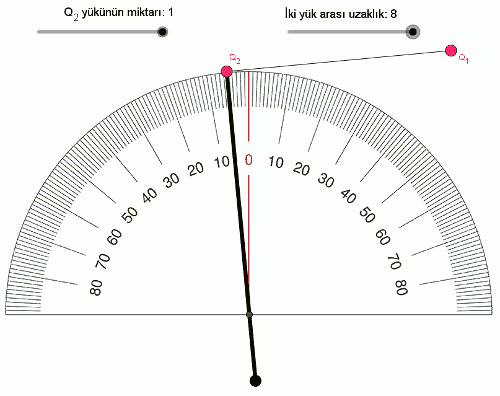
Daha çok veri noktamız olduğu için bu sıralı ikilileri (mesafe,açı) bir tabloya yazalım.

Mesafe	Açı
2	86
2,5	55
3	38
3,5	28
4	21
4,5	17
5	13
5,5	11
6	10
6,5	8
7	7
7,5	6
8	5

Şimdi de bu verinin grafiğini çizelim:

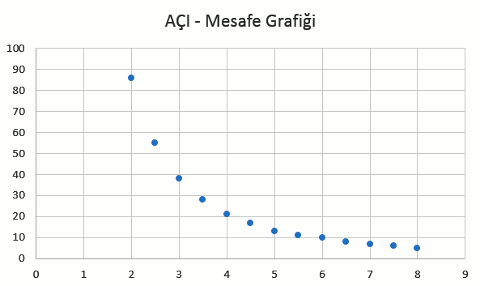
Bu grafik kesinlikle doğrusal görünmüyor. Uzaklık arttıkça açının ne kadar hızlı azaldığına dikkat edin. Öyleyse buna bir başka model oturtmalıyız, üssel fonksiyon denediğimde şöyle bir grafik elde ettim:

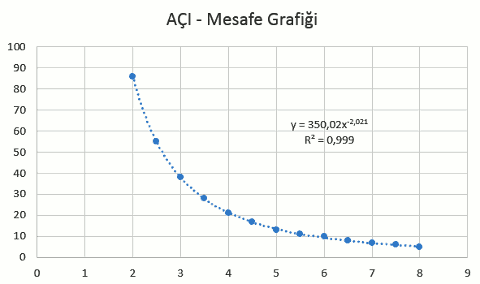
Bu grafikteki modelde y = (350)x^-2 çıktığını görüyorum (rakamları yuvarladım). R² = 0,999 çıkmış, yani bu model bu veriye çok iyi oturmuş. y = mx^{-2} = m\frac{1}{x^2} olduğuna dikkat edin. Öyleyse, elektriksel kuvvet yüklerin arasındaki uzaklığın karesiyle ters orantılı. Buna ters kare kanunu da deniyor, kütle çekim kuvveti de bir başka ters kare kanunu.

F \space \alpha \space \frac{1}{x^2}

Şimdi bu deneyden öğrendiklerimizi birleştirelim ve Coulumb kuvveti nelere bağlıdır sorusuna cevap verelim:

1. Elektriksel kuvvet yüklerin çarpımıyla doğru orantılı
2. Elektriksel kuvvet yüklerin arasındaki mesafenin karesiyle ters orantılı

F \space \alpha \space q_1q_2\frac{1}{x^2} F \space \alpha \space \frac{q_1q_2}{x^2}

Bu Coulomb kanunun genel ifadesi. Ancak elektriksel kuvvet ile yüklerin çarpımı ve arasındaki mesafenin oranını gösteren bir de sabit katsayı var. Artık orantı değil eşitlikten söz edebiliriz ve Coulumb kuvvetinin formülünü şöyle yazabiliriz:

F = k \frac{q_1q_2}{x^2}

k katsayısına Coulomb katsayısı deniyor, büyüklüğü de

k = 9.10⁹ m²/C²

Bu katsayının bu kadar büyük olmasının nedeni (9.000.000.000) Coulumb biriminin çok büyük miktarda yükü ifade ediyor olması. Bizim karşılaştığımız yükler genellikle nC (nano Coulomb) ya da (mikro Coulomb) mertebesinde oluyor. Dolayısıyla Newton olarak ölçtüğümüz kuvveti gösterebilmesi için de böyle büyük bir katsayıyla çarpılarak büyütülmesi gerekiyor. Yani küçücük miktardaki yükler kocaman elektriksel kuvvet uyguluyor.

Ayrıca bu katsayı yüklerin içinde bulunduğu ortama göre de değişiyor. k= 9.10⁹ C²/m² boşluk (içinde madde olmayan uzay) için geçerli olan değer, eğer yükleri bir maddenin içine (su veya cam gibi) koyarsanız bu değer değişiyor.

Son olarak Coulumb kuvveti ile ilgili deneylerimizde hep aynı cins yük kullandık. Eğer deneyleri zıt yüklü cisimler için tekrar etseydik, elektriksel kuvvetin büyüklüğünün aynı kaldığını ama yönünün değiştiğini görecektik. Aşağıdaki resimler sırayla üç farklı olasılığı gösteriyor. İlk resimde iki artı yük birbirini eşit büyüklükte ve zıt yönlü kuvvetlerle itiyor. Dikkat etmeniz gereken yüklerin büyüklüğünün eşit olması gerekmediği.

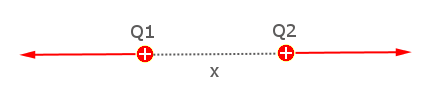
Aşağıdaki resimde bu kez iki eksi yük görüyoruz. Bu iki eksi yük de tıpkı artı yüklerde olduğu gibi birbirlerini eşit büyüklükte ve zıt yönlerde itiyor.

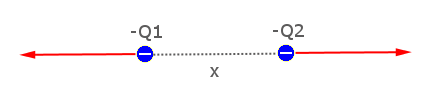
Son olarak bu resimde biri artı, diğer eksi iki yüklü cisim görüyoruz. Bu yükler birbirlerini eşit büyüklükte ve zıt yönde (buna dikkat gerçekten yönleri zıt mı?) kuvvetlerle çekiyorlar.

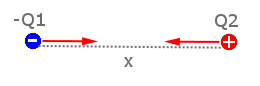
Her durumda Newton’un üçüncü yasası etki tepki prensibi geçerli. İki cisim etkileştiğinde birbirlerine eşit büyüklükte ama zıt yönde kuvvetler uyguluyorlar.

Elektriksel kuvvet ve Coulomb Kanunu ile ilgili Simülasyonlar

• Bu simülasyon İtalyanca ama gayet açık oynamanızı tavsiye ederim, bu yazıdaki Coulomb deneyi bununla yapıldı.
• Bu simülasyon Yunanca ama bu da gayet açık, iki eksi yük, iki artı yük ve bir artı bir eksi yük durumunda uygulanan Coulomb kuvvetinin yönünü ve büyüklüğünü gösteriyor.

Elektriksel kuvvet ve Coulomb Kanunu ile ilgili kazanımlar

2018 – 9.6.1.3. Elektrik yüklü cisimler arasındaki etkileşimi açıklar.

• Deneyler veya simülasyonlardan yararlanılarak elektrik yüklü cisimler arasındaki etkileşimin (Coulomb Kuvveti) bağlı olduğu değişkenler arasındaki ilişkiyi belirlemeleri sağlanır. Matematiksel model verilir.
• Yüklerin etkileşimi ile ilgili matematiksel hesaplamalara girilmez.
• Yüklerin etkileşimi ile ilgili hesaplamalar yapılması sağlanır. (Fen lisesi)

Bu konu hem 9. sınıfta hem de 11. sınıfta var.
2018 – 11.2.1.1. Yüklü cisimler arasındaki elektriksel kuvveti etkileyen değişkenleri belirler.

• Öğrencilerin deney veya simülasyonlardan yararlanmaları sağlanır.
• Coulomb sabitinin (k), ortamın elektriksel geçirgenliği ile ilişkisi vurgulanır.