Sağ el kuralı fizikte ve matematikte kullandığımız bir hatırlama aracıdır. Neyi hatırlama? Üç boyuttaki eksenleri. Şimdiye kadar bir ve iki boyuttaki vektörlerle çalışmıştınız. Tork, manyetizma ve açısal momentum kavramlarına gelince, kaçınılmaz olarak üçüncü boyut işin içine giriyor. Çünkü bu kavramlarda aynı düzlemdeki iki vektörün vektörel çarpımı söz konusu. Sağ el kuralı iki vektörün vektörel çarpımı sonucunda ortaya çıkan çarpım vektörünün yönünü belirlemede yardımcı oluyor.
Vektörel Çarpım
Önce matematiksel olarak vektörel çarpımı tanıyalım. Aynı düzlemdeki iki vektörün vektörel çarpımı, her iki vektöre de diktir.
\vec{A} \times \vec{B} = \vec{C}
A vektörü x eksenine paralel, B vektörü y eksenine paralel olursa, ikisinin vektörel çarpımı olan C vektörü z eksenine paralel olur, yani x – y eksenlerinin oluşturduğu düzleme dik olur. Bunun anlamı C vektörünün aynı anda hem A hem de B vektörüne dik olduğudur. Aşağıdaki resimde sağ elimizi kullanarak bu üç vektörü nasıl gösterebileceğimizi görüyoruz.
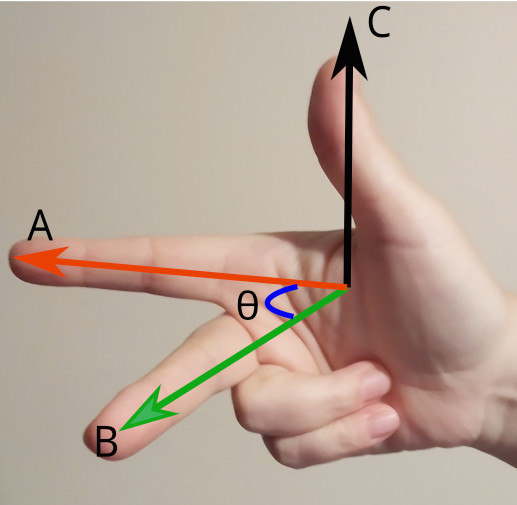
Vektörel çarpımda değişme özelliği yoktur. Yani:
\vec{A} \times \vec{B} \ne \vec{B} \times \vec{A}
Dolayısıyla vektörlerin çarpımdaki sırası önemlidir. Sağ el kuralı bize bunu hatırlatır. Sağ elimizin işaret parmağı birinci vektörü (A), orta parmağımız ikinci vektörü (B) gösterecek şekilde tutulduğunda, baş parmağımız vektörel çarpım vektörünün (C) yönünü gösterir.
Vektörel çarpımda eğer iki vektörün yerini değiştirirsek, çarpım vektörünün yönü ters döner. A vektörüyle B vektörünün vektörel çarpımı C ise, B vektörüyle A vektörünün çarpımı -C olur. Eksi işaretine dikkat edin, yönünün zıt olduğunu gösteriyor.
\vec{B} \times \vec{A} = - \vec{C}
Bu durumu sağ el kuralıyla şöyle gösterebiliriz.
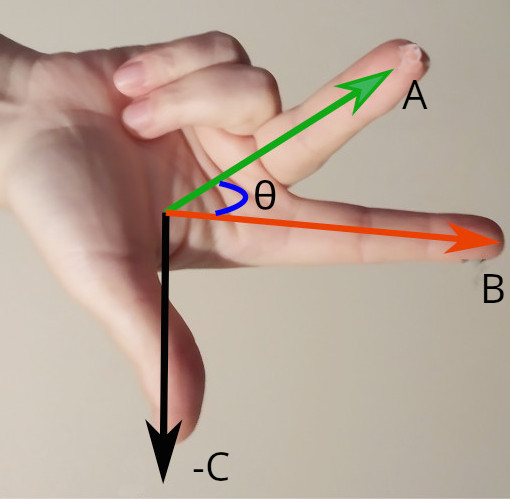
Dikkat edin, gerektiğinde elimizi çevirmemiz gerekiyor. Bu durumda tam ters çevirdik sağ elimizi. B vektörünün işaret parmağımızı, A vektörünün orta parmağımızı göstermesi gerekiyordu çünkü. Böylece iki vektörün çarpımının -C vektörü olduğunu bulabildik.
İkinci Yöntem
Eğer siz de benim gibi orta parmağınızı dik tutmakta zorlanıyorsanız, sağ el kuralını uygulamanın bir yolu daha var. Onu da aşağıdaki resimde görelim.
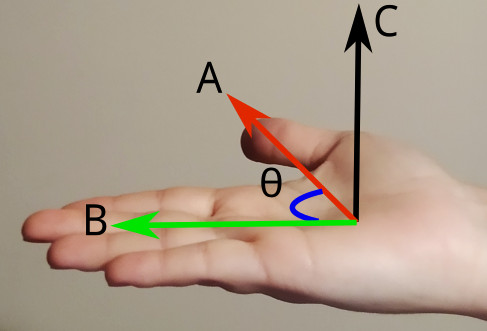
Bu kez avcunuzu açıyorsunuz. İlk vektörü (A) baş parmağınızın, ikinci vektörü (B) diğer parmaklarınızın yönünde yerleştiriyorsunuz. Sonra avcunuzla yukarı doğru ittiriyorsunuz. Avcunuzun gösterdiği yön vektörel çarpımın sonucunun (C) yönü oluyor.
Üçüncü Yöntem
Son olarak sağ el kuralında parmakların dönme yönüyle belirleme yönteminden bahsedelim. Aşağıda A ve B vektörleri gösteriliyor. A x B vektörel çarpımının yönünü bulacağız.
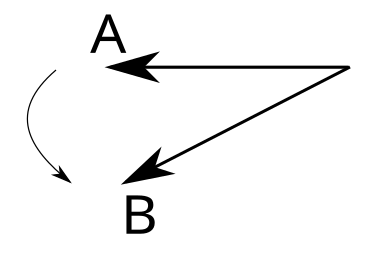
Bu yöntemde ilk vektörün (A) yönünde dört parmağımızı uzatıyoruz. Sonra ikinci vektörün (B) yönünde parmaklarımızı kıvırıyoruz. Baş parmağımız A ve B vektörlerinin çarpımının (C) yönünü gösteriyor. Sağ elimizin dört parmağını saat yönünün tersinde kıvırıyoruz.

Bir de tam ters duruma bakalım. Aşağıdaki vektörlerin vektörel çarpımının yönünü bulalım.
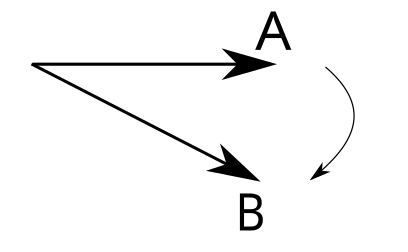
Bu kez A’dan B’ye doğru saat yönünde kıvırmak zorundayız sağ elimizin parmaklarını. Bunu sağ elinizle yapabilmenizin tek yolu elinizi ters çevirmek. Aşağıdaki resimde gösterildiği gibi.

Sağ el kuralını anlamanın yolu pratik yapmaktan geçiyor. Denerken elinizin ve bedeninizin tuhaf durumlara girmesi mümkün. Deneyerek en rahat çalışacağınız yöntemi bulmak size kalıyor.
Vektörel Çarpımın Büyüklüğü
Sağ el kuralı bize iki vektörün vektörel çarpımının yönünü bulmakta çok yardımcı oluyor, ama büyüklüğüyle ilgili bir şey söylemiyor. Vektörel çarpımın büyüklüğü matematiksel olarak şöyle bulunuyor:
|\vec{A} \times \vec{B} | = |\vec{A}||\vec{B}|sin \theta
Yani A ve B vektörlerinin büyüklüklerini çarpıp, sonra iki vektörün arasındaki açının sinüsüyle çarpıyoruz. Eğer iki vektör birbirine dik olursa sin 90° = 1 olduğu için vektörel çarpımın büyüklüğü şuna dönüşüyor:
|\vec{A} \times \vec{B} | = |\vec{A}||\vec{B}|sin 90^\circ = |\vec{A}||\vec{B}|
Sağ el kuralıyla ilgili kazanımlar
10.1.4.1. Üzerinden akım geçen düz bir iletken telin oluşturduğu manyetik alanı etkileyen değişkenleri analiz eder.
- Sağ el kuralı verilir. Manyetik alanın yönü ve şiddeti ile ilgili matematiksel hesaplamalara girilmez.
11.1.8.1. Tork kavramını açıklar.
- Torkun yönünü belirlemek için sağ el kuralı verilir.
11.2.4.1. Üzerinden akım geçen iletken düz bir telin çevresinde, halkanın merkezinde ve akım makarasının (bobin) merkez ekseninde oluşan manyetik alanın şiddetini etkileyen değişkenleri analiz eder.
- Manyetik alan yönünün sağ el kuralıyla gösterilmesi sağlanır.
11.2.4.3. Üzerinden akım geçen iletken düz bir tele manyetik alanda etki eden kuvvetin yönünün ve şiddetinin bağlı olduğu değişkenleri analiz eder.
- Manyetik kuvvetin büyüklüğünün matematiksel modeli verilir, sağ el kuralının uygulanması sağlanır.
11.2.4.5. Yüklü parçacıkların manyetik alan içindeki hareketini analiz eder.
- Öğrencilerin, sağ el kuralını kullanarak yüklü parçacıklara etki eden manyetik kuvvetin yönünü bulmaları ve bu kuvvetin etkisiyle yükün manyetik alandaki yörüngesini çizmeleri sağlanır.