Açısal momentum dönme hareketinde ortaya çıkan bir fiziksel büyüklüktür. Öteleme hareketinde çizgisel momentumdan bahsetmiştik, bu yazıda önce açısal momentumu tanımlayacağız, sonra çizgisel momentum ile ilişkilendireceğiz. Bu büyüklük korunduğu için fizikteki en önemli büyüklüklerden biri olarak karşımıza çıkıyor, atomları anlamaktan galaksileri incelemeye kadar bir çok alanda kullanıyoruz. Aşağıdaki resimde düzgün çembersel hareket yapan bir cisim gösteriliyor. Bu cismin kütlesi m, dönme hareketinin yarıçapı r ve cismin çizgisel sürati de v.
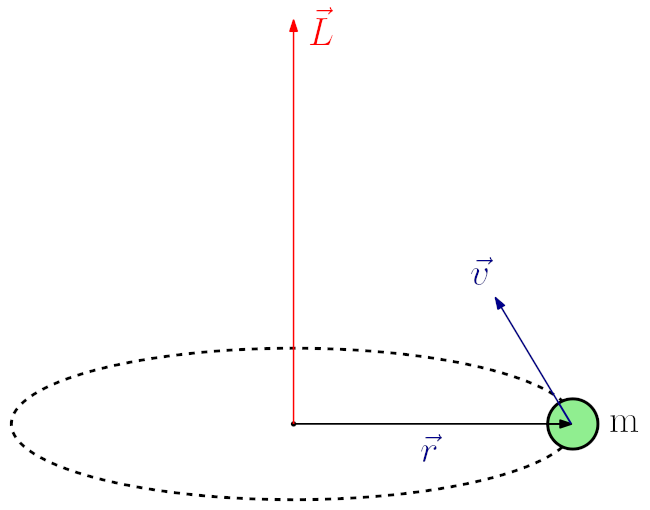
Bu cisim için açısal momentumun formülü (matematiksel modeli ya da tanımı) şöyle:
\vec{L} = \vec{r} \times \vec{P} = \vec{r} \times m\vec{v}
Şimdi ne demek bu formül açıklayalım. Öncelikle L ile gösteriliyor ve vektörel bir büyüklük (kırmızı vektör). Konum vektörüyle (yarıçap konum vektörü r) çizgisel momentum vektörünün (P) çarpımına eşit. Açısal momentum vektörünün yönünü sağ el kuralı ile buluyoruz, yönü hem konum vektörüne hem de çizgisel momentum vektörüne dik. Bu cisim saat yönünün tersinde dönme hareketi yapıyor olsaydı açısal momentum vektörünün yönü ne tarafa doğru olurdu? Cevaplarınızı yorumlarda bekliyorum. L’nin büyüklüğü de mvr’ye eşit. L = mvr. En önemli noktalardan biri açısal momentumun olabilmesi için (yani sıfır olmaması için) cismin mutlaka dönme hareketi yapıyor olması. Diğer bir nokta da eğer dönme eksenini değiştirirseniz yarıçap vektörü değişir dolayısıyla açısal momentum da değişir. Son olarak açısal momentumun biriminin kgm2/s olduğunu da ekleyelim.
Örnek soru 1
Sürtünmelerin önemsiz olduğu yatay bir düzlemde, 2 kg kütleli bir cisim 4 m yarıçaplı bir yörüngede düzgün çembersel hareket yapmaktadır. Cismin çizgisel sürati 20 m/s ise açısal momentumu kaç kgm2/s olur?
Çözüm
Açısal momentumun formülünü hatırlayalım:
L = mvr
Gerisi sadece formülde bildiğimiz değerleri yerine koymak.
L = (2kg)(20m/s)(4m) = 160 kgm^2/s
Açısal momentum ile Eylemsizlik momenti arasındaki ilişki nasıldır?
Dönme hareketini incelerken, öteleme hareketinin analogu olan büyüklükleri kullanıyoruz. Örneğin çizgisel hız yerine açısal hız, kuvvet yerine tork, kütle yerine eylemsizlik momenti gibi. Öyleyse momentumda P = mv yaptığımız gibi L için de eylemsizlik momenti (I) cinsinden ne yazabiliriz?
\vec{L} = \vec{r} \times m \vec{v}
Çizgisel hızı açısal hız cinsinden yazalım:
\vec{v} = \omega r
Yerine koyalım:
L = r \times m (\omega r) = (mr^2)\omega
Eylemsizlik momenti neydi, hatırlayın:
I = mr^2
Öyleyse:
L = I\omega
Aslında L ve w vektörel büyüklükler ve yönleri de aynı, eylemsizlik momenti ise skaler bir büyüklük:
\vec{L} = I\vec{\omega}
P = mv öteleme hareketinde momentumun tanımıydı, dönme hareketinde ise L = Iw açısal momentumun tanımı oldu.
Örnek soru 2
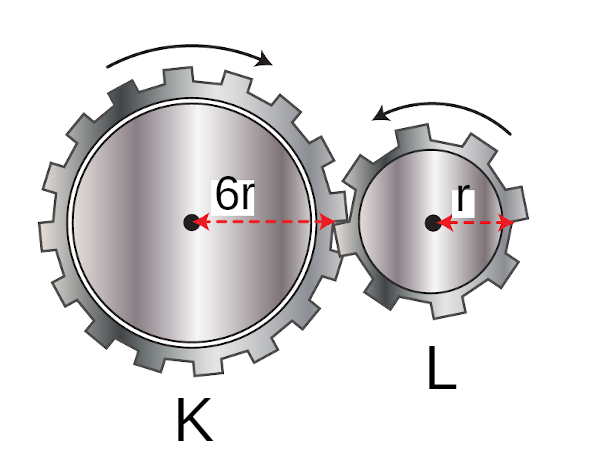
Şekildeki K ve L dişlileri birlikte dönerken açısal momentumları eşit oluyor. K dişilisinin eylemsizlik momenti IK L dişlisininki IL ise, IK/ IL oranı kaçtır?
Çözüm
Açısal momentumların eşit olduğunu biliyoruz. Öyleyse:
L_K = L_L
Bu durumda dişlilerin açısal hızlarını bulmamız gerekir. K dişlisi bir tur attığında aldığı yol:
2 \pi 6r = 12 \pi r
Bu yol L dişlisinin de aldığı yola eşit, çünkü birlikte dönüyorlar. Öyleyse:
\omega_K = \frac{12\pi r}{6r} = 2\pi; \omega_L = \frac{12\pi r}{r} = 12\pi
Şimdi yerine yerleştirelim:
\frac{I_K}{I_L} = \frac{\omega _L}{\omega_K} = \frac{12 \pi}{2 \pi} = 6
Açısal ivme nedir?
Açısal hızı tanımlamıştık, şimdi karşımıza açısal ivme çıktı. Şimdi önce açısal hızı hatırlayalım, sonra açısal ivmeyi tanımlayalım. Açısal hız birim zamanda değişen açı demekti yani:
\omega = \frac{\Delta \theta}{\Delta t}
Açısal ivme ise birim zamanda değişen açısal hız demek. Biriminin de radyan bölü saniye kare (rad/s2) ya da 1 bölü saniye (1/2) olduğuna dikkat edin. Çünkü açısal hızın birimi rad/s idi, bir kez daha zamana (s) bölünce bu çıkıyor.
\alpha = \frac{\Delta \omega}{\Delta t} = \frac{\omega_{son} - \omega_{ilk} }{t_{son} - t_{ilk}}
Düzgün çembersel harekette açısal hız sabit olduğu için açısal ivme sıfırdı. Ama çembersel hareket illa düzgün yani sabit açısal hızlı olmak zorunda değil. Eğer cisme çizgisel hızı doğrultusunda bir kuvvet uygulanırsa cismin açısal hızı değişir dolayısıyla açısal ivme sıfırdan farklı olur. Ayrıca çizgisel ivme de sıfırdan farklı ve açısal ivme ile ilişkili. Düşünelim:
a = \frac{\Delta v}{\Delta t}; v = r\Delta \omega; a= \frac{r\Delta \omega}{\Delta t}; a = r\alpha
Yani tıpkı çizgisel hızla açısal hız arasındaki ilişki gibi çizgisel ivme ile açısal ivme arasındaki ilişki yarıçapla doğru orantılı olması.
Açısal ivme, tork ve eylemsizlik momenti ilişkisi nasıldır?
Newton’un ikinci hareket kanununu kurcalarsak, acaba dönme hareketi için ne gibi ilişkiler elde edebiliriz. Kurcalayalım:
F = ma
Dönme hareketinde tork sürekli karşımıza çıkıyordu. Bakalım tork ne yapacak:
\tau = Fr
F yerine bulduğumuz ifadeyi yazalım:
\tau = (\alpha m r)r = \alpha mr^2
Eylemsizlik momentini hatırlayalım:
I = mr^2
Bakın ne çıktı:
\tau = I \alpha
Öteleme hareketin de F = ma idi dönme hareketinde T = Iα oldu.
Örnek soru 3
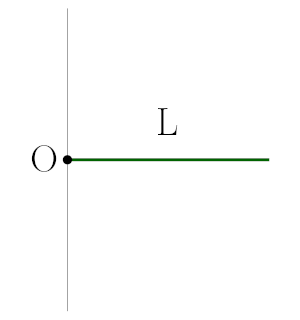
Şekilde gösterilen m kütleli L uzunluğundaki çubuk O noktası etrafında düşey düzlemde serbestçe dönebilmektedir. Çubuk serbest bırakıldığında açısal ivmesi α ve eylemsizlik momenti I oluyor. Çubuğun kütlesi iki katına yarıçapı üç katına çıkarılırsa (a) açısal ivmesi kaç α, (b) eylemsizlik momenti kaç I olur?
Çözüm
Korkmaya gerek yok. Önce soruyu bir anlamaya çalışalım. İlk durumda çubuğu serbest bırakırsak ağırlığından dolayı çubuğun ağırlık merkezine bir tork uygulanacak. Ağırlık merkezi çubuğun tam ortası yani L/2.
\tau = Fr = mg\frac{L}{2}
Ayrıca tork ile açısal ivme arasındaki ilişkiyi de biliyoruz:
\tau = I \alpha
Böylece kalsın şimdilik. Şimdi ikinci durumu inceleyelim:
\tau_2 = F_2r_2 = 2mg\frac{3L}{2} = 3mgL
Şimdi oran yapabiliriz:
\frac{3mgL}{mg\frac{L}{2}} = \frac{I_2 \alpha_2}{I \alpha} = 6
Eylemsizlik momentini düşünelim. Çubuğunkini hatırlamayabilirsiniz, soruda da verilmeyebilir, tek bilmeniz gereken mr2 ‘nin bir sabitle çarpımı olması (aynı dönme ekseni olduğunda ama).
I = Kmr^2 = KmL^2
Yani eylemsizlik momentleri oranı 18. Artık açısal ivmeyi bulmak kolay.
6I\alpha = 18I \alpha_2
Öteleme ve dönme hareketlerinin kıyaslanması
Aşağıdaki tabloda öteleme ve dönme hareketlerini incelerken kullandığımız kavramların karşılaştırması sunuluyor:
| Karşılaştırılan | Öteleme | Dönme |
|---|---|---|
| Harekete karşı gösterilen direnç | kütle (m) | eylemsizlik momenti (I) |
| Momentum | çizgisel momentum (P) | açısal momentum (L) |
| Hız | çizgisel hız (v) | açısal hız (w) |
| İvme | çizgisel ivme (a) | açısal ivme (α) |
| İvmenin sebebi (hareket durumunu değiştiren etki) | kuvvet (F) | tork (T) |
| Temel ivme denklemi | F = ma | T = Iα |
| Kinetik enerji | (1/2)mv2 | (1/2)Iw2 |
Açısal momentum ile ilgili kazanımlar
12.1.3.1. Açısal momentumun fiziksel bir nicelik olduğunu açıklar.
- Açısal momentumun atomik boyutta da fiziksel bir nicelik olduğu belirtilir.
12.1.3.2. Açısal momentumu çizgisel momentum ile ilişkilendirerek açıklar.
Kazanımlara uygun bir anlatımdı . Teşekkürler