Dönme ve Dönerek Öteleme Hareketinde Kinetik Enerji

Dönme hareketini ve dönerek öteleme hareketini incelemiştik. Şimdi bu hareket çeşitlerinde kinetik enerji nasıl bulunur formülü nedir, inceleyeceğiz. Önce kinetik enerji öteleme hareketinde nasıldı, hatırlayalım. m kütleli bir cisim h süratiyle hareket ediyorsa kinetik enerjisi şöyledir:
KE = \frac{1}{2}mv^2

Peki olduğu yerde dönen bir cismin kinetik enerjisi nasıldır? En basit haliyle düzgün çembersel hareket yapan m kütleli bir cismi inceleyelim. Aşağıdaki resimde m kütleli bir cisim r yarıçaplı bir çember etrafında v çizgisel hızıyla düzgün çember hareket yapıyor olsun. Bu cismin kinetik enerjisini nasıl buluruz?

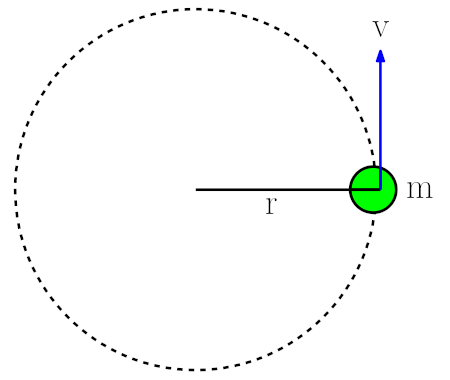
KE = \frac{1}{2}mv^2

Açısal hız ile çizgisel hız arasındaki ilişkiyi hatırlayalım:
v = \omega r

Şimdi bunu yerine yazalım:
KE = \frac{1}{2}m(\omega r)^2 = \frac{1}{2}mr^2\omega^2

Eylemsizlik momentini de öğrenmiştik. Düzgün çembersel hareket yapan böyle bir cismin eylemsizlik momenti:
I = mr^2

Bunu da yerine yazalım:
KE = \frac{1}{2}I\omega^2

Dönen bir cismin kinetik enerjisinin cismin eylemsizlik momenti ile ve açısal hızının karesiyle doğru orantılı olduğunu bulmuş olduk. Peki şimdi bir örnek çözelim.

Örnek soru 1:

m kütleli L uzunluğunda bir çubuk dönme ekseni ortasında olacak şekilde ve dönme ekseni çubuğun bir ucunda olacak şekilde döndürülüyor. Her iki durumda da kinetik enerjileri eşit olduğuna göre çubuğun birinci durumdaki açısal hızının ikinci durumdaki açısal hızına oranı kaç olur?

Çözüm

Öncelikle eylemsizlik momentlerini ezberlemenize gerek yok, bunlar sorularda verilir. Bir çubuk için dönme ekseni ortasındaysa ve ucundaysa I değerleri şöyleydi:
I_{orta} = \frac{1}{12}mL^2; I_{uc} = \frac{1}{3}mL^2

Artık kolay bu soruyu çözmek:
KE_{orta} = \frac{1}{2}(\frac{1}{12}m(\frac{L}{2})^2)\omega_{orta}^2

KE_{uc} = \frac{1}{2}(\frac{1}{3}m(\frac{L}{2})^2)\omega_{uc}^2

Kinetik enerjiler eşit olduğuna göre:
\frac{1}{2}(\frac{1}{12}m(\frac{L}{2})^2)\omega_{orta}^2 = \frac{1}{2}(\frac{1}{3}m(\frac{L}{2})^2)\omega_{uc}^2

\cancel{\frac{1}{2}}(\frac{1}{12}\cancel{m}\cancel{(\frac{L}{2})^2)}\omega_{orta}^2 = \cancel{\frac{1}{2}}(\frac{1}{3}\cancel{m}\cancel{(\frac{L}{2})^2)}\omega_{uc}^2 \frac{\omega_{orta}^2}{12} = \frac{\omega_{uc}^2}{3} \frac{\omega_{orta}^2}{\omega_{uc}^2} = \frac{12}{3} = 4 \sqrt{(\frac{\omega_{orta}}{\omega_{uc}}})^2 = \sqrt{4} = 2

Dönerek öteleme hareketinde kinetik enerji

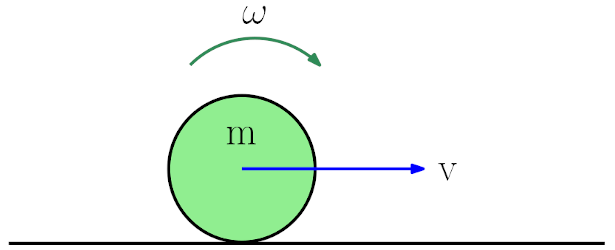
Şimdi de dönerek öteleme hareketinde kinetik enerjiyi inceleyelim. Aşağıdaki resimde m kütleli bir cisim yatay bir zeminde kaymadan dönerek öteleme hareketi yapıyor. Cismin kütle merkezinin v hızıyla gittiğini ve cismin de ω açısal hızıyla döndüğünü görüyoruz. Bu cismin kinetik enerjisi hem cismin kütle merkezinin öteleme hareketinden hem de dönme hareketinden kaynaklanıyor, dolayısıyla ikisinin toplamına eşit.

KE = \frac{1}{2}mv^2 + \frac{1}{2}I\omega^2

Örnek soru 2

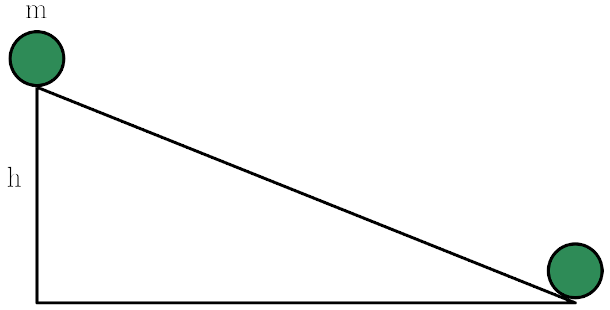
Yukarıdaki şekilde h yüksekliğinde bir eğik düzlemden içi dolu bir silindir serbest bırakılıyor. İlk durumda silindir eğik düzlemde sadece kayarak ilerliyor. İkinci durumda ise hiç kaymadan sadece dönerek hareket ediyor. Silindirin yarıçapı 1 metre ise, ilk durumda eğik düzlemin sonuna geldiğindeki hızının ikinci durumda eğik düzlemin sonuna geldiğindeki oranı kaç olur? (I=1/2mr²)

Çözüm

Silindir sadece kayıyorsa, sadece öteleme hareketi yapıyor demektir. Öyleyse kimetik enerjisi:
KE_1 = \frac{1}{2}mv_1^2

silindir sadece dönüyor hiç kaymıyorsa o zaman dönerek öteleme hareketi yapıyor demektir. Öyleyse:
KE_2 = \frac{1}{2}mv_2^2 + \frac{1}{2}I\omega^2

Başlangıçta potansiyel enerjileri aynı olduğuna göre, eğik düzlemin sonuna geldiklerinde kinetik enerjileri de aynı demektir.
KE_1 = KE_2 = mgh

Şimdi dönen silindirin açısal hızını bulalım:
v = \omega r; \omega = \frac{v}{r}

Eşitliği yazalım ve bunu yerine koyalım:
\frac{1}{2}mv_1^2 = \frac{1}{2}mv_2^2 + \frac{1}{2}I \frac{v_2^2}{r^2}

Şimdi eylemsizlik momentini yazalım:
I = \frac{1}{2}mr^2; r = 1; I = \frac{m}{2}

Tekrar düzenleyelim:
\frac{1}{2}mv_1^2 = \frac{1}{2}mv_2^2 + \frac{1}{2}\frac{m}{2} \frac{v_2^2}{1^2} = \frac{1}{4}mv_2^2

(\frac{v_1}{v_2})^2 = \frac{2}{4} = \frac{1}{2} \frac{v_1}{v_2} = \frac{1}{\sqrt{2}}

Dönme ve dönerek öteleme hareketi ile ilgili kazanımlar

12.1.2.3. Dönme ve dönerek öteleme hareketi yapan cismin kinetik enerjisinin bağlı olduğu değişkenleri açıklar.

• Matematiksel hesaplamalara girilmez.