Açısal Momentumun Korunumu nedir? Örnekler ve Gösterimler

Daha önce bir sisteme dışarıdan bir kuvvet etki etmediği sürece sistemin momentumunun sabit kaldığını yani korunduğunu öğrenmiştiniz. Dönme hareketiyle ilgili olarak da yine bir sisteme dışarıdan bir tork uygulanmadığı müddetçe açısal momentum da sabit kalır, işte açısal momentumun korunumu budur. Şimdi bir örnekle bunu inceleyelim.

 

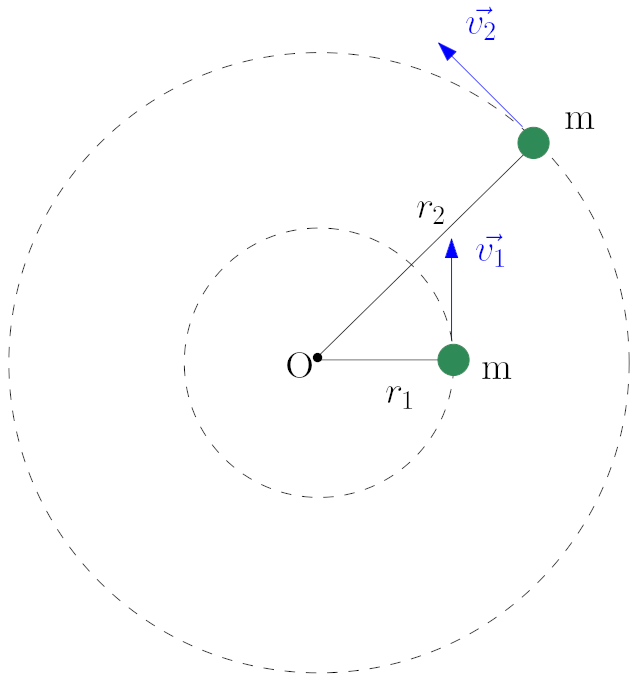
Yukarıdaki resimde m kütleli bir cisim önce O dönme ekseninde küçük r₁ yörüngesinde düzgün çembersel hareket yapıyor. Sonra aniden yarıçap büyüyor ve r₂ oluyor. Çizgisel hızlarının oranı yani v₁/v₂ ne olur? Dışarıdan bir tork uygulanmadığına göre açısal momentum korunur, yani ilk yörüngedeki açısal momentum son yörüngedekine eşit olur. Yazalım:
L = mv_1r_1 = mv_2r_2
Şimdi düzenleyelim:
\frac{v_1}{v_2} = \frac{r_2}{r_1}
Yani yarıçap artarsa çizgisel hız azalıyor; yarıçap azalırsa çizgisel hız artıyor. Peki açısal hız nasıl değişiyor?
v = \omega r

\frac{r_1}{r_2} = \frac{\omega_2 r_2}{\omega_1 r_1} \frac{\omega_1}{\omega_2} = \frac{r_2^2}{r_1^2}

Açısal hızın yarıçapların oranının karesiyle orantılı olduğunu gördük. Şimdi de açısal momentumun korunumunu günlük yaşamdan örneklerle inceleyelim.

Örnek soru

Yarıçapı 2 m olan bir yörüngede 4 m/s süratle düzgün çembersel hareket yapan 3 kg kütleli bir cisim aniden yarıçapı 1 m olan bir yörüngeye indirilerek hareketine devam ediyor. Cismin son durumda çizgisel hızı ve açısal hızı ne olur?

Çözüm

Yukarıda formülleri çıkardık. Sadece yerine koyalım. İlk açısal momentum şöyle:
L = (3 kg)(4 m/s)(2 m) = 24 kgm^2/s
Açısal momentum korunduğuna göre:
L = (3kg)(v_s)(1 m) = 3vs = 24
Öyleyse:
v_s = 8 m/s
Açısal hız da:
v = \omega r

\omega = \frac{8 m/s}{1 m} = 8 \space rad/s

Açısal momentumun korunumu video

Aslına bakarsanız, hareket eden birşeyi görmeden hareketini anlamak zor. Bu nedenle aşağıdaki videoyu izleyip okumaya öyle devam etmenizi öneririm. Yazının devamı videoyu yorumluyor.

Uzay İstasyonunda Takla atan Astronot

• Bu astronotu başka bir astronot bir sırtından bir tork uygulayarak çevirip bırakıyor.
• Astronot önce dizlerini ve kollarını gövdesinde topluyor. Böylece dönme yarıçapını azaltıyor. Bu durumda hızlı dönüyor.
• Sonra kollarını ve bacaklarını açıyor. Böylece dönme yarıçapını artırıyor. Açısal momentum korunduğu için, dönme yarıçapı artınca dönme hızı azalıyor.

Dönen taburedeki adam

• Bu adam dönen bir taburede oturuyor ellerinde de dumbeller var. Başlangıçta biri ona bir tork uygulayarak biri çeviriyor.
• İlk durumda kolları açıkken yavaş dönüyor.
• Sonra kollarını vücuduna doğru çekip topladığında dönme hızı artıyor. Çünkü açısal momentum korunuyor, yarıçap azalınca çizgisel hız artıyor.

Dönen buz patencisi

• Bu buz pantenci kolları ve bacakları açıkken yani dönme yarıçapı büyükken yavaş dönüyor.
• Kollarını ve bacaklarını içe topladığında hızlanıyor.

Açısal momentum deneyi

• Bu alet aslında önceki örneklerin ölçülebilir olanı.
• Bir çubuğun uçlarında iki kütle yerleştirilmiş.
• Kütlelere bir ip bağlı ve yukarıdaki halkadan çekince kütleler birbirine yaklaşıyor.
• Açısal momentumun, çizgisel momentumla dönme yarıçapının çarpımı olduğunu hatırlayın.
• Dönme yarıçapı azalınca çizgisel hızın arrtığını görüyoruz.
• Çünkü açısal momentum korunuyor.

Hoberman Küresi

• Bu bir Hoberman küresi.
• Altında bir ip var ve çekince küre küçülüyor.
• Küre küçüldüğünde eylemsizlik momenti de küçülüyor.
• Dolayısıyla açısal hızı artıyor.
• Çünkü açısal momentum korunuyor.

Güneş’in Etrafında Eliptik Yörüngesinde Dolanan Gezegen

• Güneşin çevresinde eliptik bir yörüngede dolanma hareketi yapan gezegenin hızına dikkat edin.
• Güneşten uzakken yani dönme yarıçapı büyükken çizgisel hızı küçük.
• Güneşe yaklaşınca dönme yarıçapı azalıyor, dolayısıyla çizgisel hızı artıyor.

Dönen taburedeki adam ve dönen bisiklet tekerleği

• Burada da bir adam bir bisiklet tekerleğini döndürüyor.
• Sonra dönen bir tabureye oturuyor.
• Bisiklet tekeri dikken adam dönmüyor.
• Ama tekeri yatay hale getirince önce sağdan sola dönmeye başlıyor.
• Tekeri tam tersine ama yine yatay hale getirince bu kez soldan sağa dönmeye başlıyor.
• Çünkü teker ve adamdan oluşan sistemin açısal momentumu korunuyor.

Dönerken düşmeyen bisiklet tekeri

• Burada da bisiklet tekeri bir ipe bağlanmış.
• Teker dönmediğinde teker düşüyor.
• Ama teker döndürüldüğünde düşmüyor.

Jiroskop

• Bu da irice bir jiroskop.
• Jiroskop dönmediğinde dengede kalamıyor, düşüyor.
• Ama döndürüldüğünde düşmüyor, dengede kalabiliyor.
• Çünkü açısal momentum korunuyor.

Açısal momentumun korunumuyla ilgili kazanımlar

12.1.3.4. Açısal momentumun korunumunu günlük hayattan örneklerle açıklar.

• Açısal momentumun korunumu ile ilgili matematiksel hesaplamalara girilmez.