Momentumun korunumu yasası nedir?

Momentumun korunumu yasası kapalı (yalıtılmış) bir sistemde toplam çizgisel momentumun zamana göre değişmeyeceğini anlatır. Yalıtılmış bir sistemin başlangıç momentumunun büyüklüğü ve yönü sistem kendi içinde etkileşse bile hep aynı kalır. Burada kendi içinde etkileşmek önemli bir nokta, bu etkileşimlere iç kuvvetler diyoruz. İç kuvvetler çarpışma, iç patlama, kenetlenme, birbirini itme gibi durumlarda karşımıza çıkar. Kapalı sistemin tanımı da hiç dış kuvvet olmayan sistemdir, çerçeve dış kuvvet olmayacak şekilde çizilir. Kapalı bir sistemde hiç dış itme bulunmaz. Momentumun korunumu kavramını örneklerle açıklayalım. Arada da örnek sorular çözelim.

Momentum ve etki – tepki yasası ilişkisi nasıldır?

Momentumun bir cismin kütlesi ve hızının çarpımı olduğunu öğrendiniz. Daha önce Newton’un üçüncü yasası olan etki – tepki kanunu da öğrenmiştiniz. Etki tepki yasası kuvvetlerin daima çiftler halinde geldiğini söyler. Bir cisim ikinci bir cisme kuvvet uyguladığında (etki), ikinci cisim de ilk cisme eşit büyüklükte ve zıt yönde bir kuvvet (tepki) uygular. Aşağıdaki resimde iki astronot yerçekimsiz ortamda birbirini itiyor. Biri diğerini ittiğinde her ikisi de kendi ittikleri yönün zıt yönünde hareket etmeye başlıyorlar. Aşağıdaki resim ittikleri anı gösteriyor. Soldaki lacivert tişötrlü astronot yeşil ok yönünde itince, kendisi sarı ok yönünde hareket etmeye başlıyor. Beyaz tişörtlü astronot da sarı ok yönünde itiyor, ardından yeşil ok yönünde geriye doğru gidiyor. Neden böyle oluyor?

İtme ve momentum kavramlarını kullanarak anlamaya çalışalım. Önce kuvvet çiftini yazalım. sağdaki astronota 1 soldakine 2 diyelim.
\vec{F_1} = - \vec{F_2}
Şimdi denklemin her iki yanını etkileşim süresiyle çarpalım.
\vec{F_1}\Delta t = - \vec{F_2}\Delta t
İtmenin momentum değişimine eşit olduğunu biliyoruz. Öyleyse:
\Delta \vec{p_1} = - \Delta \vec{p_2}
Şimdi değişimleri son ve ilk momentumların farkı olarak yazalım:
\vec{p_{1son}} - \vec{p_{1ilk}} = -( \vec{p_{2son}} - \vec{p_{2ilk}})
Düzenleyelim:
\vec{p_{1son}} - \vec{p_{1ilk}} = - \vec{p_{2son}} + \vec{p_{2ilk}}
İlk ve son momentumları bir araya getirelim:
\vec{p_{1ilk}} + \vec{p_{2ilk}} = \vec{p_{1son}} + \vec{p_{2son}}
Daha açık yazarksak:
m_1\vec{v_{1ilk}} + m_2\vec{v_{2ilk}} = m_1\vec{v_{1son}} + m_2\vec{v_{2son}}

İlginç bir sonuca ulaştık. İki astronotun başlangıç momentumları son momentumlarına eşit çıktı. Bu bize momentumun korunduğunu gösteriyor. Korunmak demek, değişmemek demektir. Yani ilk momentum, büyüklük ve yönüyle, son momentuma daima eşit olmak zorunda. Yine hatırlatalım, bu durum yalnızca dış kuvvetlerin olmadığı kapalı sistemler için geçerli. Bir örnek soru çözerek pekiştirelim mi?

Örnek soru 1

Kütlesi 0,9 kg olan bir tüfeğin içinde kütlesi 0,005 kg olan bir mermi bulunmaktadır. Tüfek ateşlendiğinde mermi 900 m/s hızla namludan çıkıyor. Buna göre tüfeğin geri tepmesindeki hızı kaç m/s olur?

Çözüm

Bu momentumun korunumu sorusu mu? Evet. Kapalı sistemimizi tüfek + mermi olarak alacağız. Bu sisteme dışarıdan kuvvet uygulanmıyor. Tüfek ateşlendiğinde mermi tüfeğe bir kuvvet uyguluyor, tüfek de mermiye, bu kuvvetler iç kuvvetler. Bir de barutun kütlesini ihmal edeceğiz, sadece mermi ve tüfeğin kütlesini kullanacağız.

Çizgisel momentumun korunumu yasası bize ilk momentumun son momentuma eşit olacağını söylüyor.
\vec{p_{1son}} + \vec{p_{2son}} = \vec{p_{1ilk}} + \vec{p_{2ilk}}
İlk durumda tüfek de mermi de duruyor yani ilk momentumumuz her iki cisim için de sıfır. Öyleyse:
\vec{p_{1son}} + \vec{p_{2son}} = 0
Kütle ve hızları yerine koyalım:
0,9\vec{v_1} + 0,005 \vec{v_2} = 0
Merminin hızını yerleştirelim ve düzenleyelim:
0,9\vec{v_1} = -0,005(900m/s)
Artık tüfeğin geri tepme hızını bulabiliriz:
\vec{v_1}= -\frac{900(0,005)}{0,9} = - 5m/s
Hızın yönünün eksi olduğuna dikkat edin, bu, merminin hızının yönünün tersi tüfeğin geri tepme hızının yönü demek.

Patlamalarda momentumun korunumu

Bir cisim hareket ederken patlarsa parçaları nasıl hareket eder? Momentumun korunumu yasası bu durumu incelememize olanak sağlıyor. İlk momentumun son momentuma eşit olacağını bildiğimiz için parçaların momentumlarını kullanarak hızlarını bulabiliriz. Bunu bir örnek soruyla inceleyelim.

Örnek soru 2

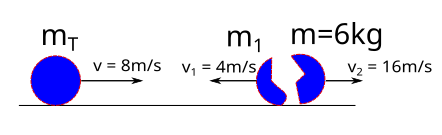
Sürtünmelerin ihmal edildiği yatay düzlemde 8m/s süratle girmekte olan bir cisim şekildeki gibi bir süre sonra bir iç patlamayla iki parçaya ayrılıyor. Kütlesi 6 kg olan parçanın hızı +16 m/s, diğer parçanın hızı -4 m/s oluyor. Buna göre cismin toplam kütlesi kaç kg’dır?

Çözüm

Momentumun korunumunu yazacağız. İlk momentumu son momentuma eşitleyeceğiz. Bu soruda bir önceki soruya göre değişen bir şey ilk momentumun sıfır olmaması.
\vec{p_{ilk}} = \vec{p_{son}}
Bildiğimiz kütle ve hız değerlerini yerlerine yazalım ama işaretlere özellikle dikkat edelim.
m_T(8) = m_1(-4) + 6(16)
Ayrıca m_T = m₁ + 6 kg
(m_1 + 6)(8) = -4m_1 + 6(16)

8m_1 + 4m_1 = 6(16 -8) 12m_1 = 6(8) m_1 = \frac{6(8)}{12}= 4 kg

Çarpışmalarda momentumun korunumu

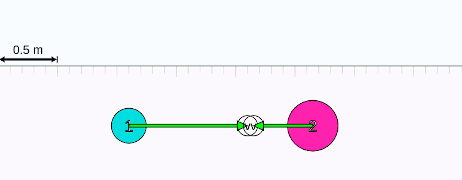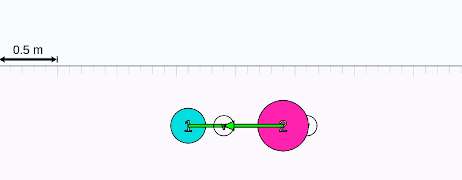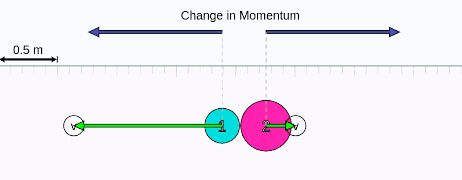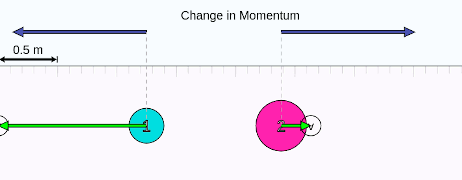
Yukarıdaki animasyonda iki cisim çarpışıyor. Çarpışmadan sonra hızları ve hareket yönleri değişiyor. Ama değişmeyen şey sistemin toplam momentumu. Animasyonda çarğışmadan hemen sonra üstte “change in momentum” yazan lacivert oklara dikkat edin. Lacivert oklar momentum değişimi vektörünü gösteriyor. Her iki cismin momentumu aslında değişiyor. Ama değişme miktarları aynı ve zıt yönlü. Toplam momentum değişimi sıfır, yani sistemin toplam momentumu değişmiyor, korunuyor. İç kuvvetler bu cisimlerin çarpışma esnasında birbirlerine uyguladıkları kuvvetler. Sistem kapalı olduğu için dış kuvvet yok.

Momentumun korunumu ve kütle merkezinin hareketi

Son olarak kapalı bir sistemde cisimlerin kütle merkezinin momentumunu inceleyeceğiz. Kütle merkezini bir kaç konu sonra ööğreneceksiniz ama kısaca burada özetleyelim. İki cismin kütle merkezi cisimler arasındaki bir doğru çizilerek bulunur. Kütle merkezinin konumu kütlesi büyük olana yakın, kütlesi uzak olandan uzaktır. Kütle merkezinin tanımıyla ilgili şimdilik bu kadarla yetinelim, daha sonraki yazımızı okursanız iyice anlayacaksınız.

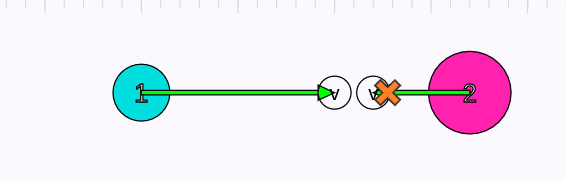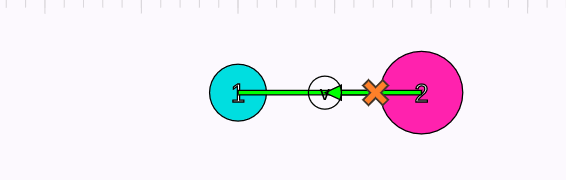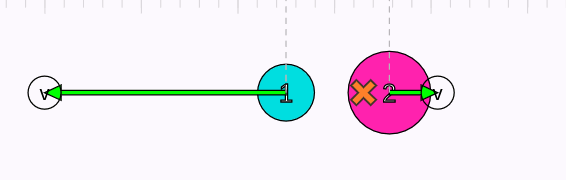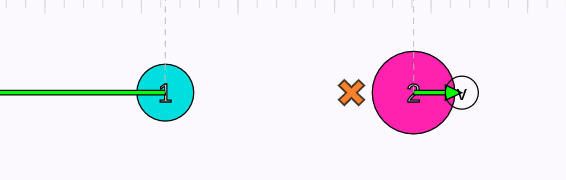
Yukarıdaki animasyonda iki cismin kütle merkezi turuncu x işaretiyle gösteriliyor. Dikkatli bakarsanız, kütle merkezinin hızının başta, ortada, sonda, yani tüm etkileşimler boyunca değişmediğini fark edebilirsiniz. Momentumun korunumunun bir sonucu da bu. Çarpışma, patlama, yapışma ne olursa olsun bir sistemin kütle merkezinin momentumu değişmiyor, dolayısıyla kütle merkezinin hızının büyüklüğü ve yönü de aynı kalıyor.

Momentumun korunumu ile ilgili bir benzetme

Günlük yaşamdan bir benzetmeyle momentumun korunumunu (aslında genel olarak tüm korunum yasalarını) biraz daha iyi anlamamız mümkün olabilir. Bu benzetmede Ahmet ve Ayşe var. Her ikisinin de cebinde 100 TL bulunuyor. Sonra Ahmet Ayşe’ye 30 TL veriyor. Ahmet’in parası 100 – 30 = 70 TL, Ayşe’ninki 100 + 30 = 130 TL oldu. Yani kişilerin cebindeki para miktarı değişti. Ama değişmeyen toplam para miktarı: 100 + 100 = 200 TL tüm süreçte aynı kaldı. Ayrıca Ayşe’nin parası +30TL, Ahmet’in parası -30TL değişti. Toplam para değişimi miktarı sıfır oldu.

Momentumun korunumu ile ilgili kazanımlar

11.1.7.3. Çizgisel momentumun korunumunu analiz eder.

• Öğrencilerin deney yaparak veya simülasyonlar kullanarak çizgisel momentum korunumu ile ilgili çıkarımda bulunmaları sağlanır.
• Çizgisel momentumun korunumu bir ve iki boyutlu hareketle sınırlandırılır.