Atışlar: yukarı ve aşağı yönlü düşey atış

Atışlar ya da atış hareketleri bir kaç alt konudan oluşuyor, ilki serbest düşmeydi, bunu inceledik. Serbest düşmenin özelliği bir cismin yüksek bir yerden sadece bırakılması, yani ilk hızının olmamasıydı. Şimdi düşey yönde bir cismi sadece bırakmakla kalmayacak ya aşağı doğru ya da yukarı doğru fırlatacağız, yani bir ilk hız vereceğiz. Yine atış hareketindeki konum zaman, hız zaman ve ivme zaman grafiklerine bakacağız ve hareket denklemlerini (formülleri) gözden geçireceğiz. Sonra da aşağı yönlü ve yukarı yönlü düşey atış ile ilgili örnek sorular çözeceğiz.

Aşağı yönlü düşey atış

Önce olayı görelim. Atışlar simülasyonunu kullanarak bir top mermisini 15 metre yükseklikten, havanın bulunmadığı bir kulenin içinde, ilk hızı 18 m/s olacak şekilde, düşey (yere dik) yönde yere doğru fırlatıyoruz. Aşağıdaki resimde bu gösteriliyor.

Sonra da bu hareket için veri toplayalım. Simülasyondaki ölçüm cihazını kullanarak eşit zaman aralıklarında top mermisinin yerden yüksekliğini bulabiliyorum. Aşağıdaki resim veriyi nasıl okuduğumu gösteriyor.

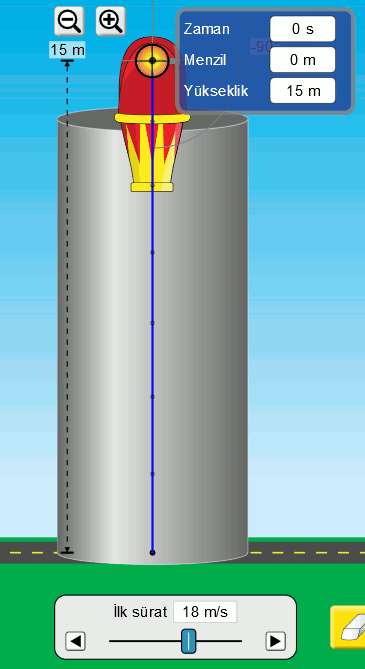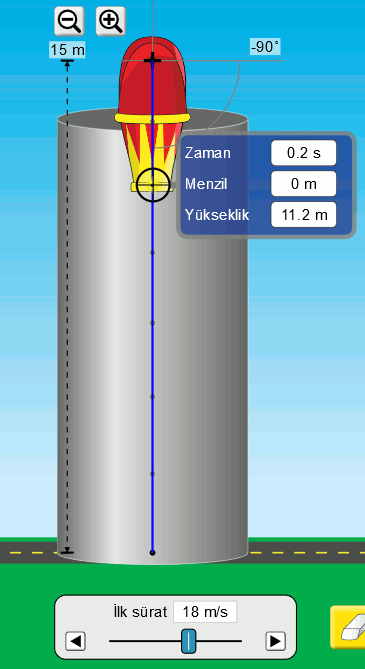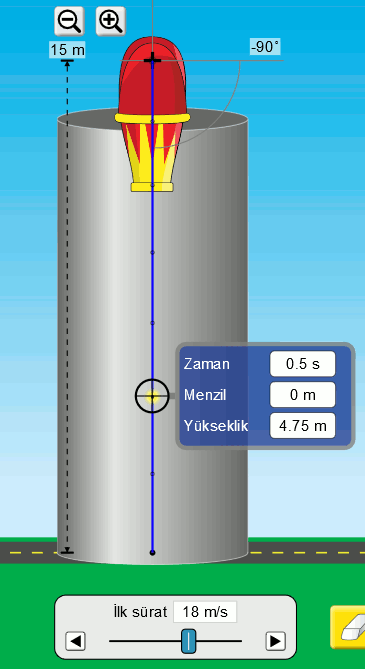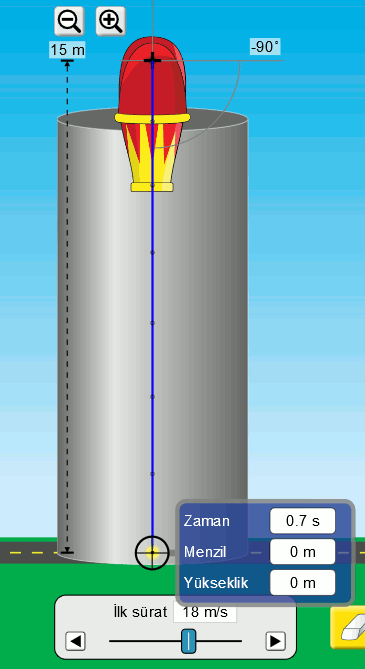
Ne zaman veri okusak, yani sayı toplasak önce bir tablo sonra da grafik çizmemiz gerektiğini biliyoruz artık. O zaman bu veriyi bir tabloya kaydedelim.

Zaman (s)	Yükseklik (m)
0	15
0,1	13,15
0,2	11,2
0,3	9,15
0,4	7
0,5	4,75
0,6	2,4
0,7	0

Konum zaman grafiği

Yukarıdaki verinin Excel’de grafiğini çizdirince şöyle görünüyor:

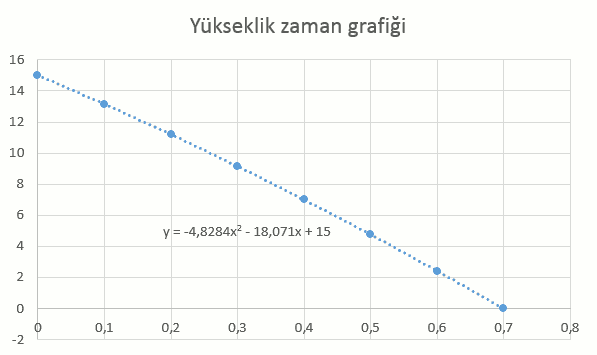
Bir de model oturttum, serbest düşmeden bildiğim üzere bu hareket sabit ivmelenen bir hareket. Bu nedenle parabol (polinom) olmak zorunda modelim. Neyse matematiğine takılmayalım ve genelleyelim. Bu model bize hareket denklemini veriyor. y = y (yani yükseklik), x = t (yani zaman).

y = -\frac{1}{2}gt^2 - 18t + 15 h = 15 \space m; v_0 = -18 \space m/s; g = 10 \space m/s^2

Öyleyse yere düştüğü zaman yani y = 0 için bu denklemi tekrar yazarsak:

0 = -\frac{1}{2}gt^2 - v_0t + h h = \frac{1}{2}gt^2 + v_0t

İşte yüksekliği, ilk hızı ve yer çekimi ivmesini matematiksel olarak birbirine bağlayan ilişkiyi yani hareket denklemini elde ettik.

Hız zaman grafiği

Artık hız denklemini de yazabiliriz. Bunu da düzgün hızlanan doğrusal harekette öğrenmiştik.

v = v_0 + gt

Bu iki denklem aşağı yönlü düşey atışı anlamamız için yetiyor.

Hız zaman grafiğini çizelim öyleyse, ama önce veri tablomuzu gösterelim. (v = 18 + 10t ile hesaplıyoruz.)

Zaman (s)	Hız (m /s)
0	18
0,1	19
0,2	20
0,3	21
0,4	22
0,5	23
0,6	24
0,7	25

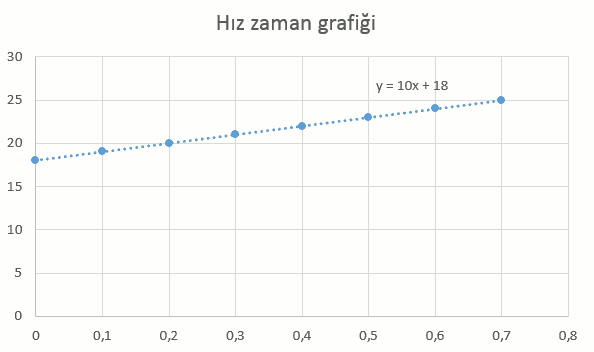
Grafiğin düzgün arttığına dikkat edin. Oturttuğum model y = 10x + 18 yani:

v(t) = 18 + 10t

Cismin herhangi bir t anındaki hızını bulabilirim bu modelle. Örneğin cimin 0,25. saniyedeki hızı:

v(0,25) = 18 + 10(0,25) = 18 + 2,5 = 20,5 \space m/s

İvme zaman grafiği

Ayrıca grafiğin eğiminin yer çekimi ivmesini, altında kalan alanın da yüksekliği verdiğine dikkat edin. Bir de ivme zaman grafiğini çizelim. İvme yer çekimi ivmesine eşit ve sabit öyleyse:

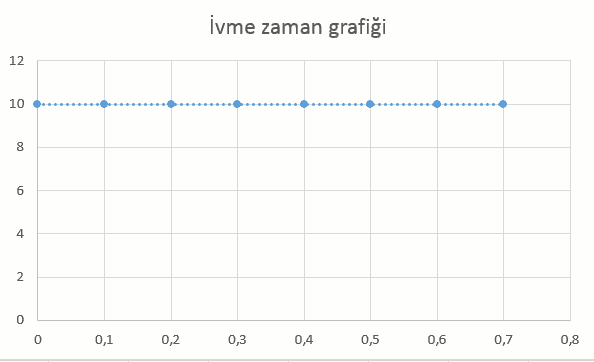
İvmenin a = g = 10 m/s² olduğuna dikkat edin.

Yukarı yönlü düşey atış

Yine önce olayı görelim. Atışlar simülasyonunu kullanarak bir top mermisini, havanın bulunmadığı bir kulenin içinde, ilk hızı 15 m/s olacak şekilde, düşey (yere dik) yönde yerden yukarı doğru fırlatıyoruz. Aşağıdaki resimde bu gösteriliyor.

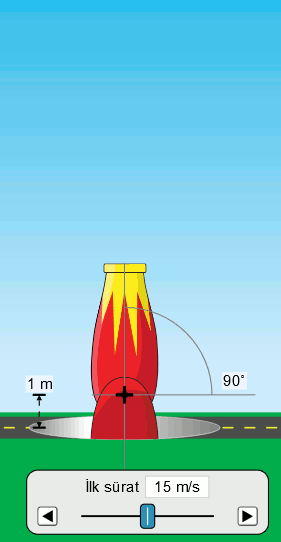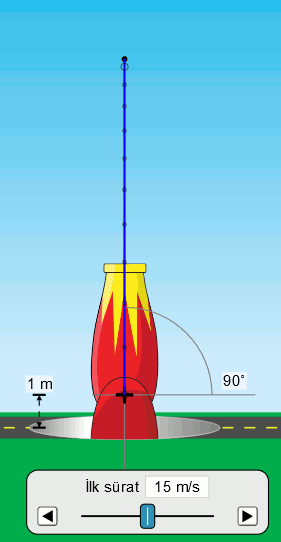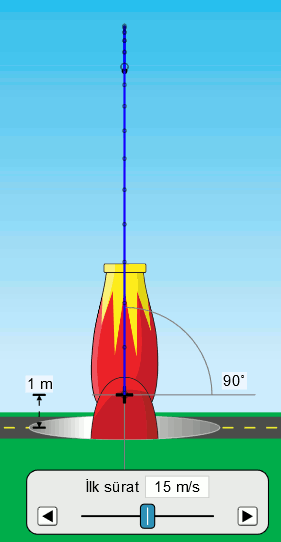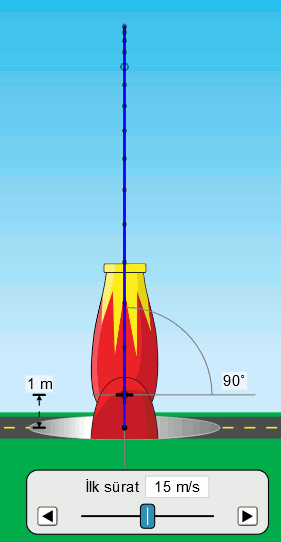
Hareketi dikkatle incelediğimizde top mermisinin fırlatıldıktan sonra önce yavaşladığını, en yüksek noktaya ulaştığında durduğunu, sonra da serbest düşme yaparak tekrar yere doğru harekete geçtiğini görüyoruz.

Nitel olarak hareketin nasıl olduğunu gördük, bir de nicel olarak (sayılarla) görelim. Elbette veri topluyoruz, zaman ve yüksekliği ölçtüm, aşağıdaki tabloya kaydettim.

Zaman (s)	Yükseklik (m)
0	0
0,1	1
0,2	2,45
0,3	3,8
0,4	5,05
0,5	6,2
0,6	7,25
0,7	8,2
0,8	9,05
0,9	9,8
1,0	10,45
1,1	11
1,2	11,45
1,3	11,8
1,4	12,05
1,5	12,25
1,6	12,05
1,7	11,8
1,8	11,45
1,9	11
2,0	10,45
2,1	9,8
2,2	9,05
2,3	8,2
2,4	7,25
2,5	6,2
2,6	5,05
2,7	3,8
2,8	2,45
2,9	1
3,0	0

Bu tablodaki sayılara anlam verebilmemiz için grafiğini çizmeliyiz.

Konum zaman grafiği

Yükseklik zaman grafiği şöyle görünüyor.

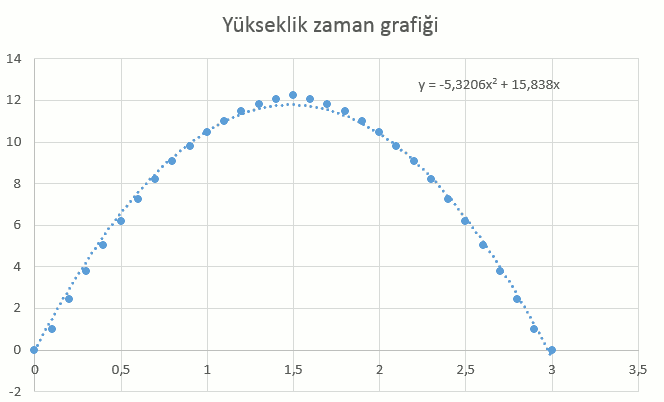
Büyük mavi noktalar veri noktalarını, kesikli çizgi ise excel’de oturttuğum modeli temsil ediyor. Bulduğum matematiksel modeli yuvarlarsam şöyle bir formül elde ediyorum:

y = -5t^2 + 15t 5 = \frac{1}{2}g y = 15t - \frac{1}{2}gt^2

15 ilk hızımız demek, yani genellersek, yukarı yönlü atış hareketinin hareket denklemini elde etmiş oluyoruz:

y = v_0t - \frac{1}{2}gt^2

İlk hızı ve yer çekimi ivmesini bilirseniz, herhangi bir t zamanında bu cismin yerden yüksekliğini bulabilirsiniz demek bu.

İlk yüksekliğimiz 0, yani yer seviyesinden atmıştık bu cismi, ama istersek bir binanın dördüncü katından da atmış olabilirdik yukarı doğru. O zaman hareket denklemimiz şöyle olurdu:

y = h_0 + v_0t - \frac{1}{2}gt^2

Burada dikkat etmeniz gereken - \frac{1}{2}gt^2 nin başındaki eksi işareti.

Hız zaman grafiği

Artık hız denklemini yazabiliriz. Bunu da düzgün yavaşlayan doğrusal harekette öğrenmiştik.

v=v_0-gt

Hız zaman grafiğini çizelim öyleyse, ama önce veri tablomuzu gösterelim. (v = 15 – 10t ile hesaplıyoruz.)

Zaman (s)	Hız (m/s)
0	15
0,1	14
0,2	13
0,3	12
0,4	11
0,5	10
0,6	9
0,7	8
0,8	7
0,9	6
1	5
1,1	4
1,2	3
1,3	2
1,4	1
1,5	0
1,6	-1
1,7	-2
1,8	-3
1,9	-4
2	-5
2,1	-6
2,2	-7
2,3	-8
2,4	-9
2,5	-10
2,6	-11
2,7	-12
2,8	-13
2,9	-14
3	-15

Şimdi de excel’de çizdiğimiz grafiği gösterelim:

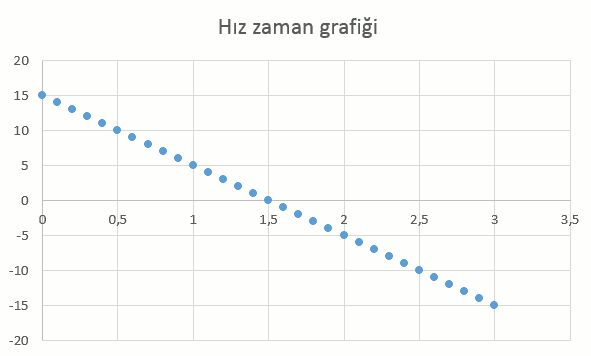
Hızın t=0 anında +15 m/s olduğu, t=1,5 s anında v=0 olduğu, t=3 anında hızın -15 m/s olduğunu grafikte görebiliyoruz. Bu grafik yukarı doğru atışta cismin önce yavaşladığını sonra geri dönüp aksi yönde hızlandığını gösteriyor.

İvme zaman grafiği

Yukarı yönlü atış hareketinde cisme uygulanan kuvvet yalnızca yer çekiminden kaynaklanan ağırlığı. Newton’un ikinci kanununa göre ivmenin büyüklüğü ve yönü sabit kalmak zorunda. Bu nedenle yer çekimi ivmesi hep yere doğru. Hız zaman grafiğinin eğimi de bu ivmeyi veriyor ve g = – 10 m/s² buluyoruz. Başındaki eksi işareti ivmenin yönünün yere doğru olduğunu, yani ilk hızla zıt yönde olduğunu gösteriyor.

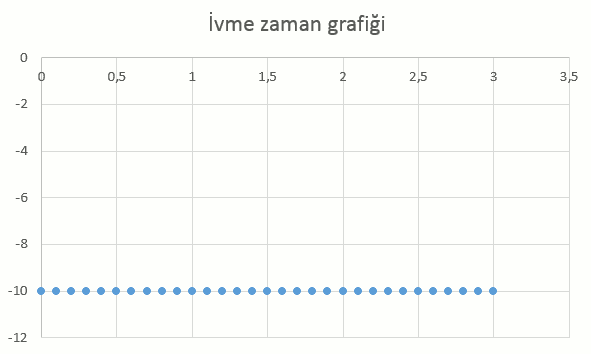
Şimdi ivme zaman neden eksi oldu diye soruyorsanız, bunun cevabı tamamen hangi yönü artı olarak seçtiğimizle ilgili. Yukarı yönü +y olarak seçtiğimiz için ivme eksi yönde oldu. Aşağı yönlü atışta aşağı yönü +y olarak seçtiğimiz için ivme de aynı yönde (aşağı doğru) olduğu için artı olmuştu.

Düşey Atış Örnek Sorular

Örnek soru 1 – Aşağı yönlü düşey atış

Hava sürtünmesinin önemsenmediği bir yerde yerden 80 m yükseklikten bir taş ilk hızı 20 m/s olacak şekilde yere dik olarak düşey doğrultuda fırlatılıyor. Taşın yere çarpma hızı kaç m/s olur?

Çözüm:

Hareket denklemini bildiğimiz için bu soru kolay. Hatırlayalım:

y = -h + v_0t + \frac{1}{2}gt^2

Yere çarptığı an dediği için y = 0 alıyoruz, çünkü y = 0 noktası taş yerde demek.

h =v_0t + \frac{1}{2}gt^2

Tüm yapmamız gereken değerleri yerleştirmek artık:

h = 80 \space m; v_0 = 20 \space m/s 80 = 20t + 5t^2

İkinci dereceden bir denklemimiz var çözelim, önce sadeleştirelim, tüm terimler 5’e bölünüyor:

t^2 + 4t - 16 = 0

Denklemin iki kökü çıkıyor:

t_1 = -6,47; t_2 = 2,47

Bunlardan anlamlı olanı ikinci kök. Çünkü eksi zamanın anlamı yok. Fizikte matematik işte böyle yorumlanıyor.

Zamanı bulduk t = 2,47 s sonra cisim yere çarpmış. Şimdi hızı bulalım:

v = v_0 + gt v = 20 + 10(2,47) v = 20 + 24,7 = 44,7 \space m/s

Büyük ihtimalle sınavlarda karşınıza daha kolay çözülecek ikinci dereceden denklemler çıkacak. Bu matematik konusu önemli iyice öğrenmenizi tavsiye ediyorum.

Örnek soru 2 – Yukarı yönlü düşey atış

Yer seviyesinden bir top ilk hızı 40 m/s olacak şekilde yukarı doğru atılıyor. (a) Topun yerden en yüksek olduğu noktanın yüksekliği kaç metredir? (b) Hareketinin 6. saniyesinde topun hızı kaç m/s dir? (Hava sürtünmesi önemsenmeyecek; g= 10 m/s²).

Çözüm:

(a) Hareket denklemini yazalım:

y = v_0t - \frac{1}{2}gt^2

Sonra da çözelim, ama zamanı bilmiyoruz. Öyleyse zamanı da hız denkleminden bulalım önce.

v = v_0 - gt

Topun yerden en yüksekte olduğu noktada durduğunu (hızının sıfır olduğunu) ve ilk hızını biliyoruz:

0 = 40 - 10t 40 = 10t t = 4 \space s

Kaç saniyede en yüksek noktaya ulaştığını bulduk, artık yüksekliği de bulabiliriz:

y = 40(4) - \frac{1}{2}10(4)^2 y =160 - 80 = 80 \space m

(b) Hareketinin 6. saniyesindeki hızını bulmak için tek yapmamız gereken hız denkleminde t=6 s değerini yerleştirmek:

v = v_0 - gt v = 40 - 10(6) v = 40 - 60 = -20 \space m/s

Hızı 20 m/s ve aşağı yönlü, eksi işareti bunu simgeliyor.

Yukarı ve aşağı yönlü düşey atış ile ilgili kazanımlar

2017 – 11.1.4.6. Düşey doğrultuda ilk hızı olan ve sabit ivmeli hareket yapan cisimlerin hareketlerini analiz eder.

• Düşey doğrultuda (yukarıdan aşağıya ve aşağıdan yukarıya) atış hareket denklemleri, konum-zaman, hız-zaman ve ivme-zaman grafikleri verilerek hesaplamalar yapılması sağlanır.