Serbest düşme nedir? Nelere bağlıdır? Örnek sorular

Bir boyutta sabit ivmeli hareketi öğrendik. Şimdi bunun en iyi uygulamalarından biri olan serbest düşme hareketini inceleyeceğiz. İnsanların serbest düşmeyi anlamaları Galileo’ya kadar mümkün olmamış. Aristo ağır cisimlerin hafif cisimlerden daha hızlı yere düşeceğini söylemiş. İnsanlar da bu fikre 1000 yılı aşkın bir süre inanmışlar. Galileo bunun böyle olmadığını hareketle ilgili deneyleri sırasında fark etmiş. İkisi de demirden yapılmış bir büyük bir de küçük topu Pisa kulesinden serbest bırakmış ve ikisinin de aynı anda yere düştüğünü gözlemiş. Hatta zamanı ölçebilmek için su saatini icat ettikten sonra Galileo’nun serbest düşme kanunu diye bilinen bir ilişkiyi de ortaya atmış. Bu yazıda bu kanunu inceleyeceğiz. Sonra da Newton’un hareket kanunlarını kullanarak serbest düşmenin neden bu şekilde çalıştığını açıklayacağız. Serbest düşme formülleri yani hareket denklemlerini vereceğiz ve örnek sorular çözeceğiz. Ama önce olayın kendisini görelim.

Hava sürtünmesi olmayan ortamda serbest düşme hareketi

Havanın olmadığı bir yer hayal etmemiz gerekiyor. Günlük hayatımızda böyle bir yer yok. Ama Amerika Birleşik Devletleri’nin Ohio Eyaletindeki Clevaland Şehrinde NASA’nın bir laboratuvarında, içinde havanın neredeyse hiç olmamasını sağlayabildikleri kocaman bir kule yapmışlar. Bu kulenin içindeki havayı çok güçlü pompalarla emiyorlar ve 3 ton havayı boşaltabiliyorlar. Koca kulenin içinde sadece 2 gram civarı hava kalıyormuş. Aşağıdaki videoda bir bowling topuyla kuş tüylerinin içinde hava bulunmayan kulenin içinde aynı anda bırakıldığında nasıl düştüklerini gösteriyor.

Bunu ne zaman seyretsem tüylerim diken diken oluyor. Çünkü Galileo ve Newton böyle bir şeyi hiç göremedi. Ama böyle düşmeleri gerektiğini fizik kanunlarını ve matematiği kullanarak öngördüler. Çok ağır olan bowling topuyla, hafif olan kuş tüylerinin onlarca metre yükseklikten bırakıldıklarında aynı anda yere düştüklerini görüyoruz. Bunun nedeni her iki cismin (bowling topu ve kuş tüyü) üzerine yalnızca yer çekimi kuvvetinin uygulanıyor olması, yani tek kuvvet ağırlık. Newton’un ikinci kanununa göre:

\vec{F} = m\vec{a} \vec{F} = m\vec{g} m\vec{g} = m\vec{a} \vec{a} = \vec{g}

Yani ivme kütleden bağımsız. Kaç kilogram olursa olsun serbest düşen bir cismin ivmesi yer çekimi ivmesine eşit olmak zorunda.

Serbest düşme hareketinin konum zaman grafiği ve hareket denklemleri

Serbest düşme olayını gördük ama sayılarla ifade etmedik. Şimdi bunu yapalım. Sayıları Atışlar Simülasyonunu kullanarak elde edebiliriz. Aşağıdaki resimde bu simülasyonda serbest düşme hareketi görülüyor.

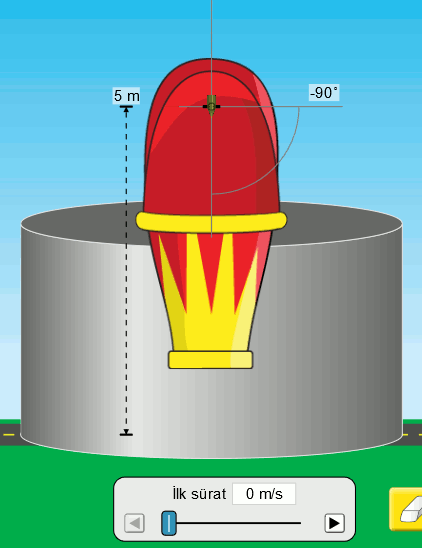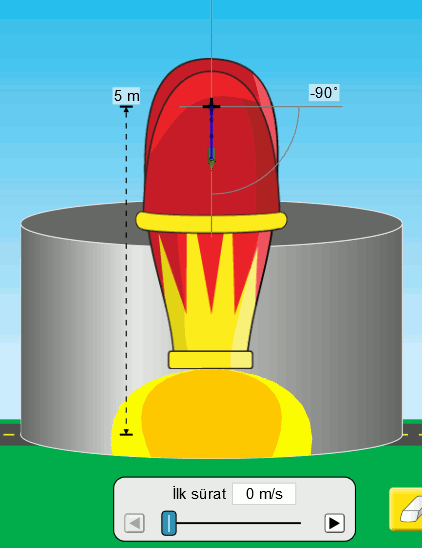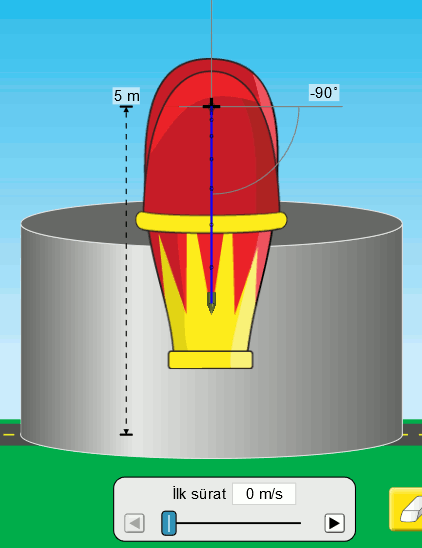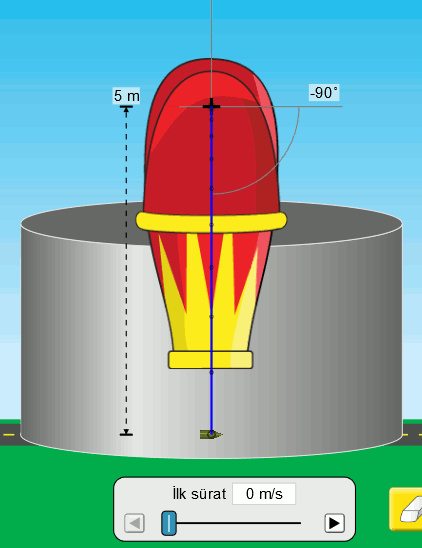
İlk sürati (hızın büyüklüğü) sıfır olan bir tank mermisini havasız ortamda serbest bırakıyoruz. Serbest düşmede ilk hız hep sıfırdır. Mermi yerden 5 metre yükseklikten bırakılıyor. Lacivert çizgi merminin yörüngesini (hareketinin izini) gösteriyor. Bu çizginin üstündeki noktalar ise eşit zaman aralıklarında merminin konumunu gösteriyor. Bir de simülasyonda ölçüm cihazını kullanarak yükseklik ve zaman değerlerini görelim.

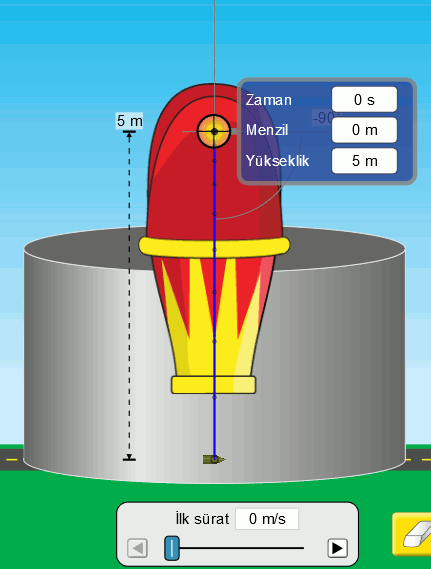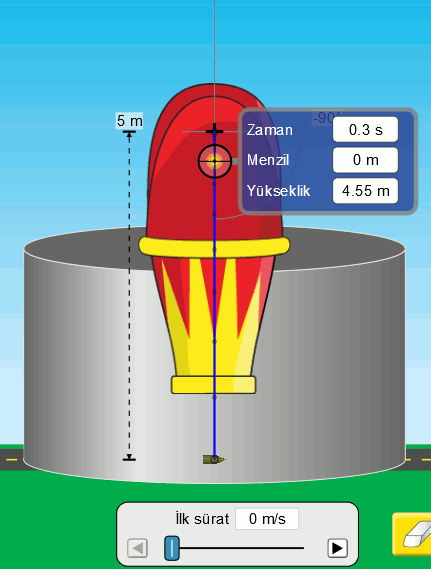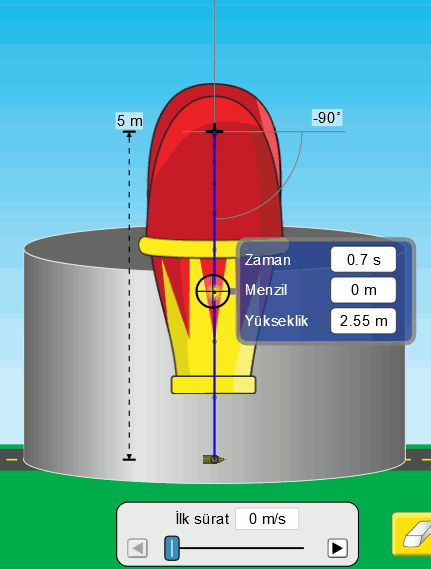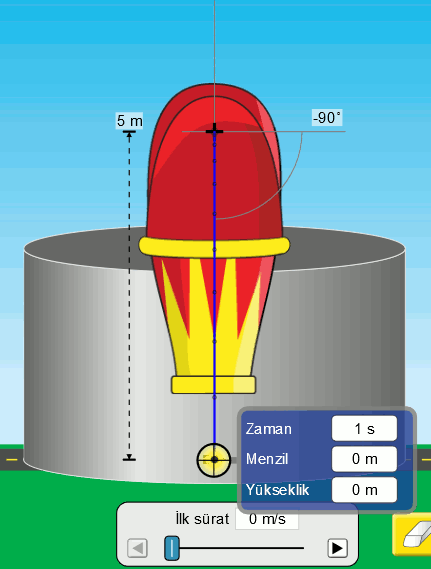
Resimden okuması zor olduğu için bu veriyi bir tabloya yazmak lazım.

t (s)	h (m)
0	5
0,1	4,95
0,2	4,8
0,3	4,55
0,4	4,2
0,5	3,75
0,6	3,2
0,7	2,55
0,8	1,8
0,9	0,95
1	0

Tabloda veriyi gördük ama sayılar arasında bir ilişki, bir düzenlilik var mı diye tabii ki grafiğini çizmemiz lazım. Konum zaman (yani yükseklik zaman) grafiği şöyle görünüyor.

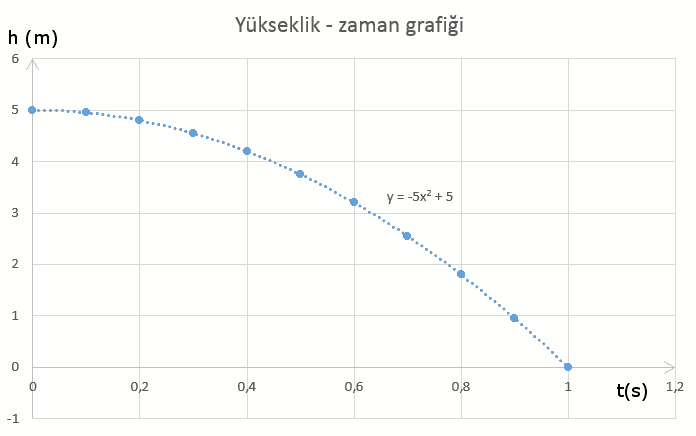
Bu grafiğe excelde bir de eğilim çizgisi (yani matematiksel model) oturttum. Bulduğum model bir parabol, denklemi de şöyle:

y = -5t^2+5

Ne demek şimdi bu denklem? Birlikte anlamaya çalışalım. y konum yani yükseklik demek, t de zaman yani geçen süre. Şimdi t = 0 yani başlangıç anında ne oluyor bu denklem ona bakalım.

y = 5 \space m

Bu t = 0 anında cismin konumunun yerden 5 m yüksekte olduğunu söylüyor. Peki y = 0 olunca ne olur?

0 = -5t^2 + 5 5t^2 = 5 t^2 = 1 \sqrt{t^2} = 1 t = 1 \space s

Yani cisim y = 0 konumuna ulaştığında (yani yere düştüğünde) geçen zaman t = 1 s oluyormuş. Bu denklem bize cismin ne zaman yere düşeceğini söylüyor.

Şimdi bunu nasıl genelleyebiliriz. Öyle bir ifade bulalım ki bize hangi yükseklikten bırakılırsa bırrakılsın, serbest düşen bir cismin hareketini öngörebilme gücü versin. Hareket denklemlerini yazmaktan bahsediyorum. Konum ve zaman ilişkisi için ivmeyi kullanmalıyız. Herhangi bir h yüksekliği için:

y = -5t^2+h

Yere çarptığı anda y = 0 olacağı için:

h = 5t^2

Buna Galileo’nun serbest düşme kanunu denmiş zamanında. Şimdi bunu Newton’un bulduğu daha resmi haline dönüştürelim.

g = 10 \space m/s^2 5 = \frac{1}{2}g h = \frac{1}{2}gt^2

İşte yükseklikle zaman arasındaki ilişkiyi gösteren hareket denklemini bulduk.

Serbest düşme hareketinin hız zaman grafiği

Serbest düşme hareketinin düzgün hızlanan doğrusal hareket olduğunu fark etmiş olmalısınız. Hız değerini bulabilmemiz ivme ve zamanın çarpımına bağlıydı.

v = at

İvme yer çekimi ivmesine eşit olduğuna göre:

v = gt g = 10 \space m/s^2

Öyleyse hız zaman verisi de şu tablodaki gibi olmalı:

t (s)	v (m/s)
0	5
0,1	1
0,2	2
0,3	3
0,4	4
0,5	5
0,6	6
0,7	7
0,8	8
0,9	9
1	10

Grafiğini çizersek (aslında sürat zaman çizdiğimize dikkat edin):

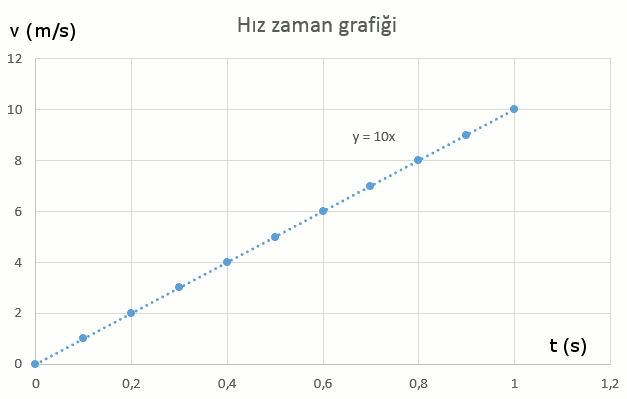
İkinci hareket denklemini (excel de oturttuğum matematiksel modelin y = 10x² olduğuna dikkat edin) bulabiliriz bu grafikten.

v = 10 t g = 10 \space m/s^2 v = gt

Serbest düşme hareketinin ivme zaman grafiği

Serbest düşmenin ivme zaman grafiği her bir boyutta sabit ivmeyle hareket eden cisminki gibi, yani sabit. Yine de önce ivme ile zaman ilişkisini gösteren veri tablosunu gösterelim.

t (s)	a (m/s2)
0	10
0,1	10
0,2	10
0,3	10
0,4	10
0,5	10
0,6	10
0,7	10
10	1,8
0,9	10
1	10

Şimdi de ivme zaman grafiğini çizelim (yine ivmenin sadece büyüklüğünü gösteriyoruz bu grafikte):

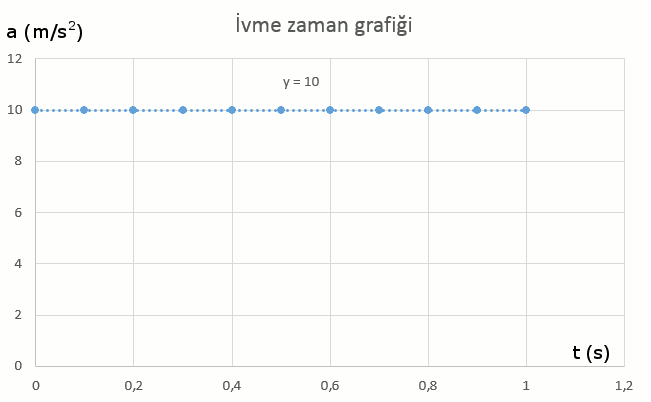
y = 10 demek aslında a = 10 m/s² demek. Yani a = g. Serbest düşen tüm cisimlerin ivmesi (hava sürtünmesini ihmal ediyoruz hatırlayın) here zaman yer çekimi ivmesine eşit olur. Hoş biz g = 10 m/s² olarak aldık ama aslında g = 9,81 m/s²dir.

Serbest düşme örnek soru

Hava sürtünmesinin ihmal edildiği bir ortamda yerden 80 m yüksekten bırakılan 10 kg kütleli bir cisim, (a) bırakıldıktan kaç saniye sonra yere düşer? (b) Hareketinin 2. ve 3. saniyeleri arasında kaç metre yol alır? (g = 10 m/s²)

Çözüm:

(a) Öncelikle kütleyle hiç bir işimiz yok. Hareket denklemimiz bize yeter.

h = \frac{1}{2}gt^2 h = 80 \space m; g = 10 \space m/s^2 80 = \frac{1}{2}10t^2 t^2 = \frac{80}{5} = 16 t = \sqrt{16} = 4 \space s

(b) Bunu iki şekilde çözebiliriz. Biri hareket denklemini kullanarak, diğeri hız zaman grafiğini çizip 2. ve 3. saniye arasında kalan alanı hesaplayarak. Ben ilk yöntemle çözeyim, size de ikinci yöntemle çözmeniz için meydan okuyayım. Yorumlarda çözümünüzü gönderebilirsiniz.

t = 2 s için:

h(2) = \frac{1}{2}10(2^2) = 20 \space m h(3) = \frac{1}{2}10(3^2) = 45 \space m

Bize sorulan h(3) – h(2) = ?

h(3) – h(2) = 45 m – 20 m = 25 m

Serbest düşme ile ilgili kazanımlar

2017 – 11.1.4.3. Hava direncinin ihmal edildiği ortamda düşen cisimlerin hareketlerini analiz eder.

• İlk hızsız bırakılan cisimler için hareket denklemleri, konum-zaman, hız-zaman ve ivme-zaman grafikleri verilerek hesaplamalar yapılması sağlanır.​