Düzgün Elektrik Alan nedir? Örnekler ve Soru Çözümleri

Elektrik alanı birim yük başına düşen elektriksel kuvvet olarak tanımlamıştık. Ama sadece noktasal yüklerin elektrik alanını incelemiştik. Noktasal yükler için elektrik alan düzgün değildir çıkarımını yapabiliriz çünkü alan uzaklığın karesiyle ters orantılı. Yani noktasal yüklerden farklı uzaklıklarda elektrik alanın büyüklüğü ve yönü değişebilir. Bu yazıda düzgün elektrik alanı inceleyeceğiz. Yani elektrik alanın büyüklüğünün ve yönünün uzayın belli bir bölgesinde sabit olduğu, hep aynı kaldığı durumu. Bu durumu nasıl oluşturabiliriz? Bunun bir yolu zıt yüklü iki paralel levhayı karşılıklı koymaktır. Neyi kastettiğimi aşağıdaki resimleri kullanarak açıklayayım.

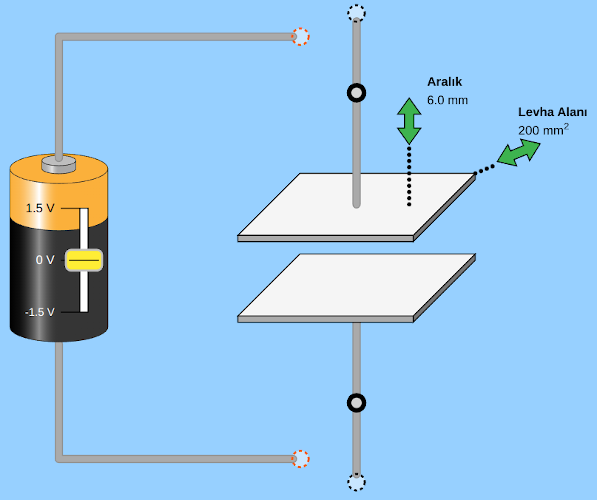
Yukarıdaki resimde iki iletken levhayı (alüminyum folyo olabilir bu levhalar) karşılıklı koymuşuz. İki levhanın arasında hiçbir şey yok, birbirlerine dokunmuyorlar. Aralarında 6 mm mesafe var. Levhalara birer tel bağlamışız, bir de pil yerleştirmişiz, ama henüz devreyi tamamlamamışız, pilin uçlarını levhalara bağlamamışız. Bağlayınca ne olur, aşağıdaki resim bağlandığı andan hemen sonra ne olduğunu gösteriyor.

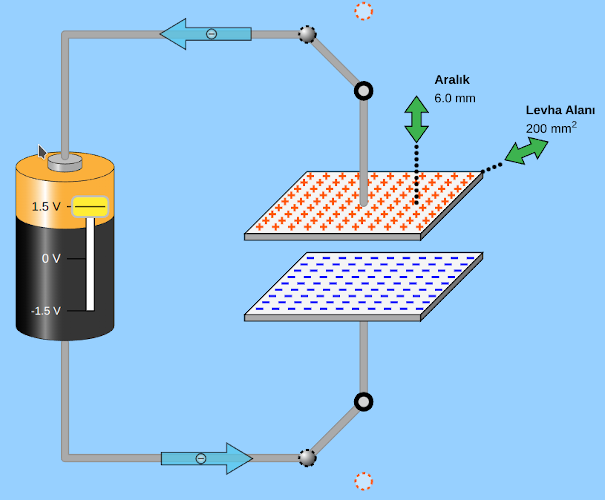
Şimdi anahtarı kapalı konuma getirip devreyi tamamladık. Pil 1.5 Volt potansiyel fark sağlıyor, başlangıçta elektrik potansiyeli sıfır olan levhalarda yükler hareket etmeye başlıyor. Üstteki levhadan elektronlar pilin artı ucuna hareket ediyor. Üstteki levhanın elektronları eksildiği için artı yükleniyor. Ne olduğunu tam anlayamadıysanız durgun elektrik konusundaki elektriklenme çeşitleri yazısına bir göz atmak isteyebilirsiniz. Alttaki levhaya ise pilin eksi ucundan elektronlar hareket ediyor, böylece alttaki levha da eksi yükleniyor. Yükler levhaların arasındaki potansiyel fark, pilin potansiyel farkına eşit olana kadar devam ediyor, sonra duruyor. Yükler hareket ederken devreden bir akım geçiyor, ama levhalar tamamen yüklenince artık yük hareketi olmadığı için akım sıfır oluyor. Hatırlamak için elektrik akımı yazısını okumak isteyebilirsiniz. Sonunda bu iki zıt yüklü paralel levha arasında aşağıdaki resimde görülen biçimde düzgün bir elektrik alan oluşuyor.

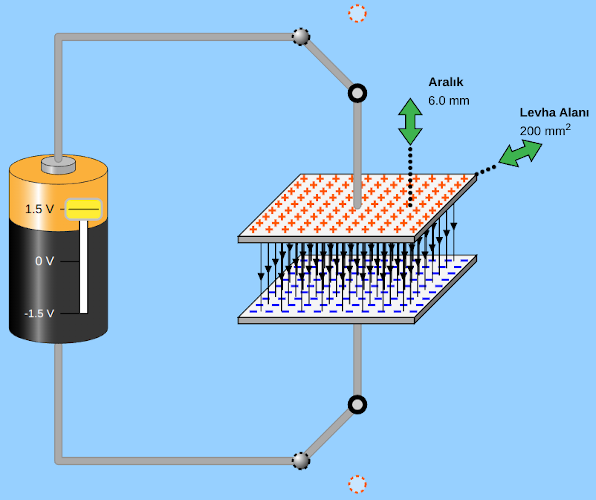
Üstteki resimde artık akım yok devrede. Üstteki artı yüklü levhadan çıkıp alttaki eksi yüklü levhaya doğru çizilen düz oklar levhalar arasındaki elektrik alanı gösteriyor. Elektrik alan vektörünün yönü artıdan eksiye doğru. Bu iki levha arasında oluşan elektrik alanın büyüklüğü ve yönü her noktada (levhaların kenarları hariç) aynı. İşte buna düzgün elektrik alan diyoruz. Yukarıdaki resimlerde üç boyutta levhaları gösterdik, şimdi de kitaplarda ve sınavlarda göreceğiniz şekilde iki boyutlu bir resimle gösterelim.

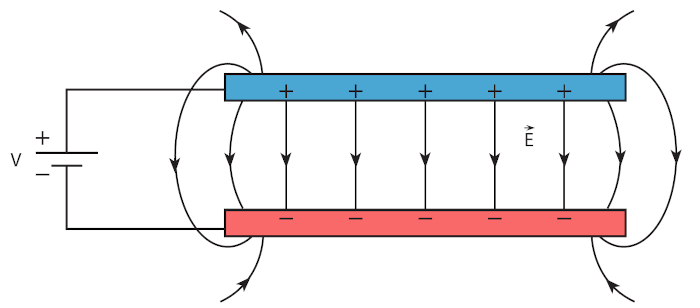
Levhaların ortasında elektrik alan düzgün, değişmiyor. Kenarlarında saçak etkisi dediğimiz bir olgudan dolayı elektrik alan düzgün değil. Alan çizgilerinin elektrik alanın düzgün olduğu yerlerde levhaların yüzeyine dik olduğuna dikkat edin. Bu çizgilerin de bir model olduğunu unutmayın, gerçekte böyle çizgi falan yok, biz anlamak için modelliyoruz. Modellerken alan çizgilerini birbirine paralel ve eşit aralıklarla çiziyoruz elektrik alanın düzgün olduğunu göstermek için. Çizgilerin artı yüklü levhadan çıkıp eksi yüklü levhaya girdiklerini de tekrar hatırlatalım.

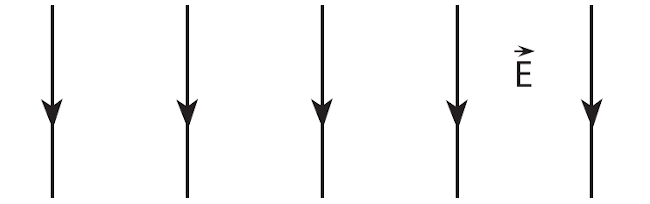
Son olarak levhalar olmadan düzgün elektrik alanı göstermek istesek ne yapıyoruz onun da resmini sunalım. Levhaları kaldırıyoruz, çizgileri bırakıyoruz, hepsi bu.

Yüklü İletken Paralel Levhalar Arasında Oluşan Düzgün Elektrik Alan Hangi Değişkenlere Bağlıdır?

Başlıktaki soruyu cevaplamak için Phet Sığa Deneyi simülasyonundan faydalanacağız. Önce levhalar arasındaki potansiyel farkı kontrol edip (yani sabit tutup) levhalar arasındaki mesafeyi (yani aralığı) değiştireceğiz. Aşağıdaki resimde bu durumu görüyoruz. İlk durumda (resmin en solunda) levhalar arası mesafe (aralık) 10 mm iken üst levhada bir miktar artı yük alt levhada da bir miktar eksi yük görüyoruz. Levhalar arasındaki siyah oklu çizgiler elektrik alanı, çizgilerin sıklığı da ne kadar elektrik alanın büyüklüğünü gösteriyor.

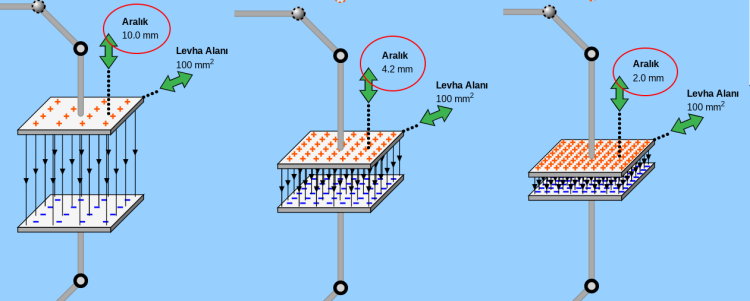
Elektrik alan çizgilerinden 16 tane sayıyorum en soldaki durumda. Ortada ise üstteki artı ve alttaki eksi yüklerin sayılarının arttığını ve elektrik alan çizgilerinin de arttığını yani sıklaştığını görüyorum. Ortadaki durumda 36 adet elektrik alan çizgisi saydım, yani elektrik alanın büyüklüğü artmış. En sağda levhalardaki yük miktarının daha da arttığını görüyorum. Elektrik alan çizgileri de artmış ve iyice sıklaşmış. Bu üç durumdan şu sonucu çıkarıyorum. Levhalar arasındaki mesafe azaldıkça elektrik alan artıyor. Tersten söylersek mesafe arttıkça elektrik alan azalıyor. Tersten söylemek neden önemli? Çünkü elektrik alanın büyüklüğünün sebebi mesafe, mesafenin sebebi elektrik alanın büyüklüğü değil. Fizikte sebep sonuç ilişkileri kuruyoruz. Burada da amacımız elektrik alanın sebeplerini belirlemek. Elektrik alan sebep değil sonuç. Ne bulduk matematiksel olarak ifade edelim. Oluşan düzgün elektrik alanın büyüklüğü levhalar arasındaki mesafe ile ters orantılı:
|\vec{E}| \space \alpha \space \frac{1}{d}
Şimdi de levhaların arasındaki mesafeyi sabit tutup levhalar arasındaki potansiyel farkı (yani voltajı) değiştirelim. Aşağıdaki resimde yine üç durum görüyoruz.

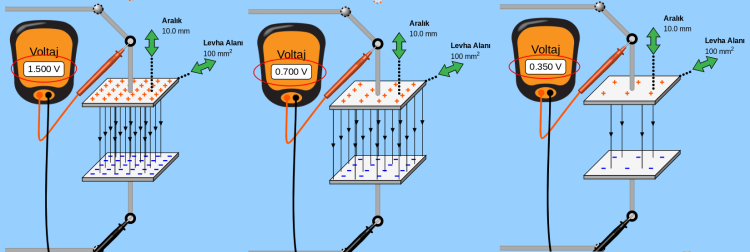
Bu kez en solda yani potansiyel fark 1.5 V iken elektrik alan çizgilerinin sık olduğunu görüyorum, bu elektrik alanın büyüklüğü yüksek demek. Ortada yani voltaj (potansiyel fark) 0.7 V iken çizgiler biraz daha seyreliyor, yani elektrik alanın büyüklüğü azalıyor. Nihayet en sağda 0.5 V voltajda elektrik alan çizgileri iyice seyreliyor, elektrik alanın büyüklüğü iyice azalıyor. Demek ki voltaj azaldıkça elektrik alanın büyüklüğü azalıyor, voltaj arttıkça elektrik alanın büyüklüğü artıyor. Yani elektrik alanın büyüklüğü levhalar arasındaki potansiyel fark ile doğru orantılı:
|\vec{E}| \space \alpha \space V
Şimdi bu iki bulguyu birleştirebilir ve düzgün elektrik alanın formülüne (matematiksel modeline) ulaşabiliriz.
|\vec{E}| = \frac{V}{d}
Bu formülde E elektrik alanın büyüklüğünü, V levhalar arasındaki potansiyel farkı (voltajı) ve d levhalar arasındaki mesafeyi (aralığı) gösteriyor. Bu bize elektrik alan için N/C (Newton bölü Coulomb) birimine eşit olan V/m (Volt bölü metre) birimini de kullanabileceğimizi söylüyor.

Bu formülü şöyle yazarsak bir başka önemli çıkarıma da ulaşabiliriz:
V = E.d
Yani düzgün bir elektrik alan içinde iki nokta alsak, bu noktalar arasındaki potansiyel farkı düzgün elektrik alanın büyüklüğüyle noktalar arasındaki yatay mesafenin çarpımı olarak bulabiliriz.

Örnek Soru: Düzgün Elektrik Alan İçinde Farklı Noktalar Arasındaki Potansiyel Farkı

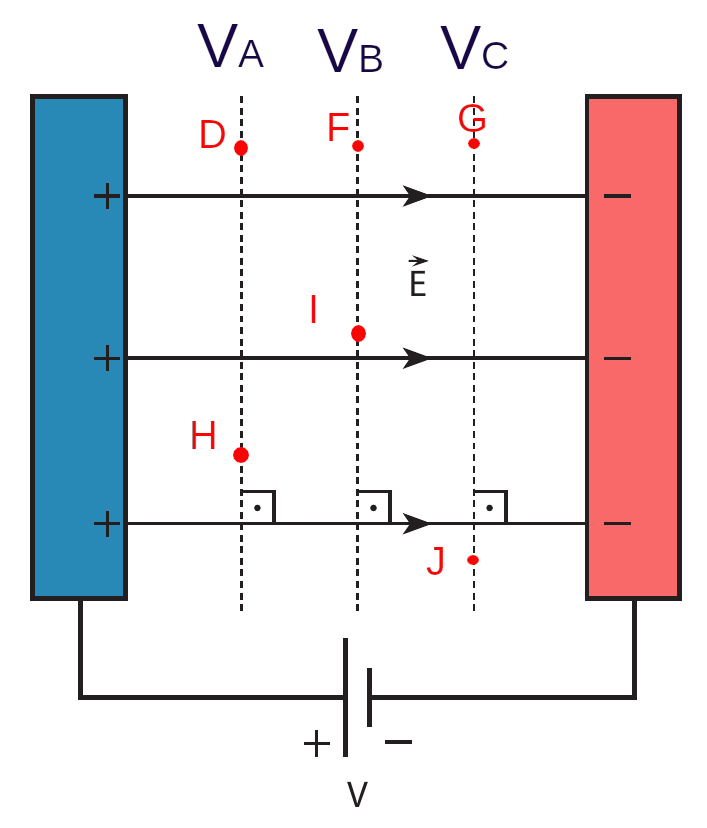
İki paralel iletken levha bir pile bağlanarak kurulan devrede levhalar arasında 5 N/C büyüklüğünde düzgün elektrik alan oluşturulmuştur. Aşağıdaki resimde gösterilen noktalar arası mesafeler |DF| = 10 cm, |FG| = 15 cm, |DI| = 20 cm, |HI| = 18 cm, |HG| = 40 cm, |HJ| = 30 cm olarak ölçülmüştür.

1. D ile H noktaları arasındaki elektriksel potansiyel fark kaç volttur?
2. F,G,H,I ve J noktalarından hangi nokta çiftleri arasındaki potansiyel fark D ile H noktaları arasındaki potansiyel farka eşittir?
3. Potansiyel fark:
   (a) D ile F arasında
   (b) F ile G arasında
   (c) D ile G arasında
   (d) H ile I arasında
   (e) H ile J arasında kaç volttur?
4. D,F ve G noktalarını büyükten küçüğe sıralayınız.

Çözüm:

1. Resimde V_A, V_B ve V_C kesikli çizgileri buralardaki eşpotansiyel çizgilerini (aslında yüzeylerini) gösteriyor. Yani her kesikli çizginin üzerindeki elektriksel potansiyelin değeri aynı. Örneğin D noktasıyla H noktasının potansiyeli aynı, ikisinin de değeri V_A. Potansiyel farkları da bu durumda sıfır demek:

V_D = V_H = V_A \Delta V_{DH} = V_A - V_A = 0

1. Aynı eşpotansiyel çizgisi üstündeki tüm noktaların potansiyellerinin eşit olduğunu biliyoruz. Soru bize potansiyel farkın sıfır olduğu nokta çiftlerini soruyor. Öyleyse tek yapmamız gereken aynı kesikli çizgilerin üstündeki noktaları belirlemek. F ile I noktalarının potansiyeli aynı (V_B); G ve J noktalarının potansiyeli aynı (V_C).
2. Bu şıkta da eşpotansiyel çizgilerini kullanacağız. Düzgün elektrik alanda eşpotansiyel çizgilerinin birbirine paralel olduklarını fark ettiniz mi? Yani bizi çapraz noktalar ilgilendirmiyor. Tek yapmamız gereken eşpotansiyel çizgileri arasındaki yatay mesafeleri kullanmak.

(a) D ile F için:
\Delta V_{DF} = V_A - V_B = Ed

d = |DF| = 10 cm \Delta V_{DF} = 5 V/m \times 0.1 m = 5 V

(b) F ile G arasındaki potansiyel farkı bulmayı size bırakıyorum. Cevabınızı yorumlarda bekliyorum.
(c). D ile G arasındaki potansiyel farkı bulmayı da size bırakıyorum. Cevabınızı yorumlarda bekliyorum.
(d) H ile I arasındaki potansiyel fark, bu iki noktanın bulunduğu eşpotansiyel çizgilerinin potansiyelleri arasındaki fark. Yani bu noktaların çapraz olmasının hiçbir önemi yok. Biz V_A ile V_B arasındaki yatay mesafeyi zaten biliyoruz, |DF| uzunluğu bu. Öyleyse:

\Delta V_{HI} = \Delta V_{DF} = V_A - V_B = Ed d = |DF| = 10 cm \Delta V_{HI} = 5 V/m \times 0.1 m = 5 V

(e) H ile J arasındaki potansiyel farkı bulmayı da size bırakıyorum. Cevabınızı yorumlarda bekliyorum.

1. Artı yüklü levhaya en yakın olan nokta olan D noktasının potansiyeli en büyük; artı yüklü levhadan en uzak olan G noktasının potansiyeli en düşüktür.

V_D > V_F > V_G

Düzgün Elektrik Alan ile İlgili Simülasyon

Sığa Deneyi (Temel Öğeler) PHET Simülasyonu düzgün elektrik alanı incelemek için harika bir araç. Oynamanızı öneriyorum.

İlgili Kazanımlar

• 11.2.3.1. Yüklü, iletken ve paralel levhalar arasında oluşan elektrik alanı, alan çizgilerini çizerek açıklar.
• 11.2.3.2. Yüklü, iletken ve paralel levhalar arasında oluşan elektrik alanının bağlı olduğu değişkenleri analiz eder. Değişkenlerin deney veya simülasyonlarla belirlenmesi sağlanır.