Elektriksel potansiyel, pozitif birim yük başına düşen elektriksel potansiyel enerji olarak tanımlanır. Tanımı enerjinin yüke oranı olduğu için, elektriksel potansiyelin SI birimi volt (V) yani joule/couloumb’tur (J/C). Önce noktasal yükler için potansiyeli inceleyelim. Durumu anlamak için bir resim kullanalım. Aşağıdaki resimde q0 ile gösterilen büyüklüğü 1 C olan bir test yükü, +q noktasal yükünden x uzaklığa yerleştirilmiş.
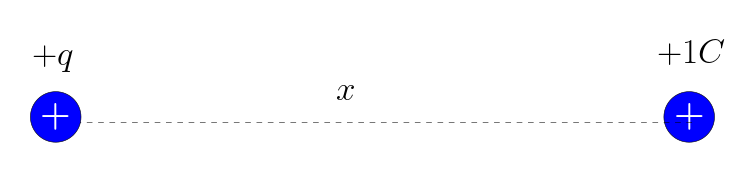
Bu konumdaki elektriksel potansiyel enerjisinin:
E_p = k\frac{qq_0}{x}
olduğunu biliyoruz. Şimdi potansiyel enerjiyi test yüküne bölelim ve potansiyeli bulalım.
V = \frac{E_p}{q_0} = k\frac{\frac{qq_0}{x}}{q_0} = k\frac{q}{x}
Demek ki bir yükün elektriksel potansiyelinin formülü şöyle:
V = k\frac{q}{x}
Asıl önemli soru elektriksel potansiyel kavramına neden ihtiyaç duyduğumuz. Zaten elektriksel potansiyel enerjiyi biliyoruz, ne diye yeni bir kavram icat ediyoruz? Bu sorunun cevabı elektrik alan kavramına çok yakın. Zaten elektriksel kuvveti biliyorduk, neden elektrik alan kavramına ihtiyaç duyduk? Elektrik alanı hatırlayalım: birim yük başına uygulanan elektriksel kuvvet.
\vec{E} = \frac{\vec{F}}{q_0}
Bir yerdeki elektrik alanı bilirsek o yere herhangi büyüklükte bir yük koyduğumuz anda yüke uygulanacak olan kuvveti de biliriz.
\vec{F} = q\vec{E}
Böylece asıl işimiz kuvvetin değil elektrik alanın haritasını çıkarmaktır. Elektrik alanın her noktada aldığı değeri gösteren bir haritamız olursa, haritada herhangi bir yere yerleştireceğimiz miktarı ne kadar olursa olsun bir yüke uygulanacak olan kuvveti hesaplayabiliriz.
Tıpkı elektrik alanın haritasını çıkardığımız gibi, elektrik potansiyelin de haritasını çıkarabiliriz. Bu durumda haritada bir yükü nereye koyarsak ne kadar elektriksel potansiyel enerjisi olacağını da hesaplayabiliriz.
E_p = qV
Elektrik konularında genellikle elektrik alan ve elektriksel potansiyel kullanılmasının nedeni, yerleştirilecek yükten bağımsız bir nicelik elde etmektir. Elektriksel potansiyelin elektrik alana göre avantajı vektörel değil skaler bir büyüklük olmasıdır. Skalerlerle işlem yapmak vektörlerle uğraşmaktan kolaydır çünkü.
Potansiyelle çalışmak birden fazla yükün olduğu durumlarda işimizi kolaylaştırabilir. Birden çok yükün bir noktada oluşturduğu elektrik potansiyeli, her yükün bireysel olarak oluşturduğu potansiyellerin toplamı olarak hesaplayabiliriz.
Örnek Soru 1
q1, q2 ve q3 noktasal yükleri aşağıdaki şekildeki gibi yerleştirilmiştir. Buna göre yüklerin A noktasında oluşturduğu elektriksel potansiyel kaç V olur?
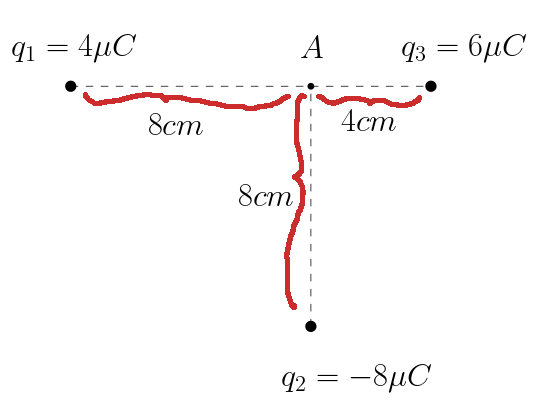
Çözüm:
A noktası için her yükün potansiyelini hesaplayıp toplayacağız.
V = k\frac{q_1}{x_1}+k\frac{q_2}{x_2}+k\frac{q_3}{x_3}
Eşpotansiyel Çizgileri ve Eşpotansiyel Yüzeyleri
Çizgi ve yüzey nereden çıktı şimdi diye merak ediyor olabilirsiniz. Harita demiştik ya, işte o haritanın en önemli özelliği bu çizgi ve yüzeyler. Resimlerini göstermeden anlatmak zor. O yüzden önce resimleri sunalım sonra açıklayalım. Aşağıdaki resimde +1nC (nano coulomb) yükün farklı mesafelerdeki eşpotansiyel çizgileri (yeşil çizgiler) gösteriliyor. Bu çizgilerin her birinin bir çember olduğunu fark etmiş olmalısınız. En içteki çizgi üzerindeki her noktada elektriksel potansiyel 33.9 V, en dıştaki çizginin üstündeki her noktada ise 5.6 V. Neden çember şeklinde tek noktasal yükün eşpotansiyel çizgileri peki? Çünkü elektriksel potansiyel değerinin birbirine eşit olduğu noktalar yükten tam olarak aynı uzaklıkta olmak zorunda, bu noktaları birleştirirseniz de bir çember elde edersiniz. Noktasal yükten uzaklaştıkça da eşpotansiyel çizgilerinin değerlerinin azaldığını görüyoruz. Bu da beklediğimiz bir şey çünkü potansiyel uzaklıkla ters orantılı.
V = k\frac{q}{r}
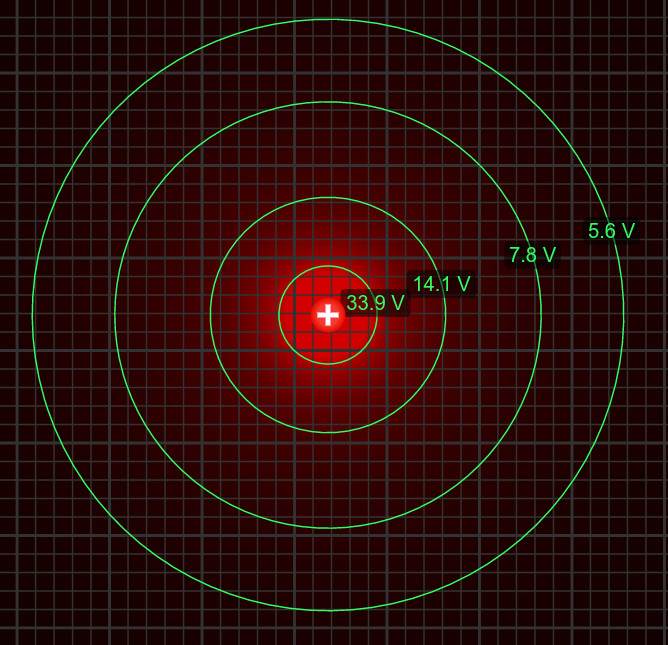
Eşpotansiyel çizgilerini gördük, çizgiler iki boyutta potansiyelin aynı olduğu yerleri bize veriyordu, tıpkı bir harita gibi. Ama gerçek dünya üç boyutlu, dolayısıyla noktasal bir yük üç boyutta küre şeklinde eşpotansiyel yüzeyleri oluşturur.
Peki bir artı bir eksi yükün (yani bir dipolün) eşpotansiyel çizgileri ve eşpotansiyel yüzeyleri neye benzer? PHET Yükler ve Alanlar Simülasyonu‘nu kullanarak çizgileri gösterebiliriz.
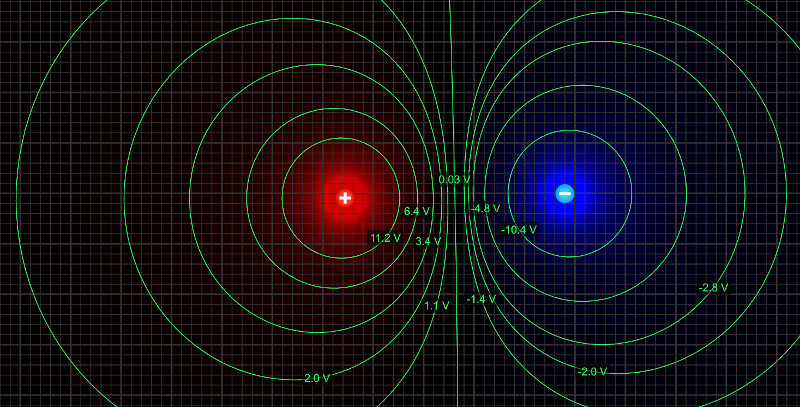
Bu kez eşpotansiyel çizgileri çember şeklinde değil. Artı yüke yakın olan yerlerdeki potansiyelin artı, eksi yüke yakın olan yerdeki potansiyelin eksi olduğuna dikkat edin. Tam ortada potansiyel neredeyse sıfır oluyor. Bir de dipolün eşpotansiyel yüzeylerini görelim.

Q1 yükü artı, Q2 yükü eksi. Eşpotansiyel yüzeyleri Q1 yükünün etrafında bir tepe biçiminde, Q2 yükünün etrafında bir çukur (ya da bir kuyu) biçiminde. yeşil çizgiler potansiyelin artı, mavi çizgiler potansiyelin eksi olduğu yerleri gösteriyor. Ortadaki siyah çizgi ise potansiyelin sıfır olduğu yerleri gösteriyor. Şimdi bu üç boyutlu temsili yorumlayalım. Bir +q noktasal yükünü Q1’e yaklaştırmak +q yükünü yokuş yukarı bir tepeye çıkarmaya benziyor, yani enerji eklerseniz ancak yaklaşabilirsiniz. Aynı +q yükünü Q2’ye yaklaştırmak ise bir çukura bırakmaya benziyor, +q kendiliğinden Q2’ye doğru yaklaşır, enerji eklemenize gerek yok. Bu resmin simülasyonunu iki yükün eş potansiyeli simülasyonunda inceleyebilirsiniz.
Bir başka önemli nokta da eşpotansiyel çizgileriyle elektrik alan arasındaki ilişki. Elektrik alanın yönü eşpotansiyel çizgilerine daima diktir.
Elektriksel Potansiyel Fark
Tekrar noktasal yükümüze dönelim. Yükümüzden farklı uzaklıkta iki nokta alalım, K ve L noktaları diyelim bunlara. Yükün K noktasındaki elektriksel potansiyeliyle L noktasındaki potansiyeli arasındaki farka (yani bildiğiniz çıkarma işlemi yapıyoruz) potansiyel fark diyoruz. Bunu eşpotansiyel resmine tekrar bakarak anlamak daha kolay olacak. Aşağıdaki resimdeki artı yüke en yakın olan çemberde bir nokta olsun K noktası, bu noktanın potansiyeli 33,9 V. L noktası da en dıştaki çemberin üstünde bir nokta olsun, bu noktanın potansiyeli de 5,6 V. K ile L arasındaki potansiyel fark şu demek öyleyse:
\Delta V_{KL} = V_L - V_K = 5,6 V - 33,9 V = -28,3 V

Potansiyel farkın pozitif çıkması L noktasının potansiyelinin K’dan daha büyük, negatif çıkması daha küçük olduğu anlamına gelir. Potansiyel farkı birim yük başına değişen potansiyel enerji olarak da tanımlayabiliriz. Bir test yükünü iç çemberden dış çembere götürmek için yapılması gereken işe de potansiyel fark diyebiliriz. Hatırlayalım zaten potansiyel fark potansiyel enerjinin birim yüke oranıydı.
E_P = qV
Elektriksel İş
Elektriksel iş bir yükü bir noktadan başka bir noktaya taşımak için aktarılması gereken enerji miktarıdır. Bunu anlamak için yine K ve L noktalarını kullanalım. Herhangi bir q yükünü K noktasından L noktasına götürmek için yapılan iş yükün miktarıyla potansiyel farkın çarpımıdır:
W = \Delta E_P = E_L - E_K
Bir örnek verelim. +2 nC bir yükü yukarıdaki resimde gösterilen 5,9 V eşpotansiyeli üstündeki bir noktadan (en dıştaki çemberden), 33,9 V eşpotansiyeli üstündeki bir noktaya (en içteki çembere) getirmek için yapılan iş:
W = 2(33,9-5,9) = 2 \times 28,3 = 56,6 J
İş pozitif çıktı, çünkü biz sisteme enerji eklemek zorundaydık. Yani 2nC yükü dış çemberden iç çembere yaklaştırabilmek için iş yapmamız gerekir, sonucunda da sistemin enerjisini artırırız. Tam tersini yaptığımızı yani iç çemberden dış çembere yükü taşımak istersek, o zaman iş negatif çıkacak, -56,6 J olacak. Peki neden? Çünkü sistem iş yapacak, sistemin enerjisi azalacak.
Örnek Soru 2
q = 3 x 10-6 C olan noktasal yük A noktasından B noktasına götürülürken 1,2 J iş yapılıyor. Buna göre A ve B noktaları arasındaki potansiyel fark kaç volttur?
Çözüm:
İş ile potansiyel fark arasındaki ilişkiyi kullanalım:
W = q\Delta V
Peki A noktasının mı yoksa B noktasının mı potansiyeli daha fazla? Neden? Cevaplarınızı yorumlarda bekliyorum.
İlgili Kazanımlar
11.2.2.1.Noktasal yükler için elektriksel potansiyel enerji, elektriksel potansiyel, elektriksel potansiyel farkı ve elektriksel iş kavramlarını açıklar.
- Kavramların günlük hayat örnekleri ile açıklanması sağlanır.
- Öğrencilerin, noktasal yüklerin bir noktada oluşturduğu elektrik potansiyeli ve eş potansiyel yüzeylerini tanımlamaları sağlanır.
11.2.2.3. Noktasal yükler için elektriksel potansiyel enerji, elektriksel potansiyel, elektriksel potansiyel farkı ve elektriksel iş ile ilgili hesaplamalar yapar.
hocam aklınıza sağlık ders kitabında bile bu kadar güzel açıklanmamış
harbiden anlaşılır ve akılda soru bırakmayacak şekilde yazmışsınız.
teşekürler