Düzgün hızlanan ve yavaşlayan doğrusal hareket nedir?

Bu konu için Kuvvet ve Hareket Temel İlkeler Simülasyonunun İvme Sekmesiyle çalışacağız. Önce düzgün hızlanan doğrusal hareket neymiş onu inceleyeceğiz.

Ben sürtünmeyi sıfır yapıp adamımızın sabit bir kuvvetle tahta kutuyu itmesini sağladım. Bu hareket esnasında da sürati ölçtüm. (İvme göstergesi de var dı onu da kullandım.) Sadece sürati bilerek bu kutu bir boyutta sabit ivmelenen (bu durumda düzgün hızlanan) hareket yapmış mıdır sorusuna cevap verebilir miyiz?

Öncelikle sürat (hızın büyüklüğü) verisini kaydettiğimizi ve bunu inceleyebileceğimizi fark etmeliyiz. Ben ilk bir saniye için şöyle bir tablo oluşturdum. Hızı her 0,025 saniyede bir ölçtüm.

t (s)	v (m/s)
t (s)	v (m/s)
0	0
0,025	0,1
0,05	0,2
0,075	0,3
0,1	0,4
0,125	0,5
0,15	0,6
0,175	0,7
0,2	0,8
0,225	0,9
0,25	1
0,275	1,1
0,3	1,2
0,325	1,3
0,35	1,4
0,375	1,5
0,4	1,6
0,425	1,7
0,45	1,8
0,475	1,9
0,5	2
0,525	2,1
0,55	2,2
0,575	2,3
0,6	2,4
0,625	2,5
0,65	2,6
0,675	2,7
0,7	2,8
0,725	2,9
0,75	3
0,775	3,1
0,8	3,2
0,825	3,3
0,85	3,4
0,875	3,5
0,9	3,6
0,925	3,7
0,95	3,8
0,975	3,9
1	4

Aslında neredeyse 2 saniyelik veri var elimde ama 41 satır girdikten sonra sıkıldım. Bu kadar veri noktası grafik çizebilmemiz için yeter de artar.

Hız zaman grafiği

Hız – zaman grafiğini çizelim, excelde dağılım grafiği çizdirince şöyle görünüyor bu veri:

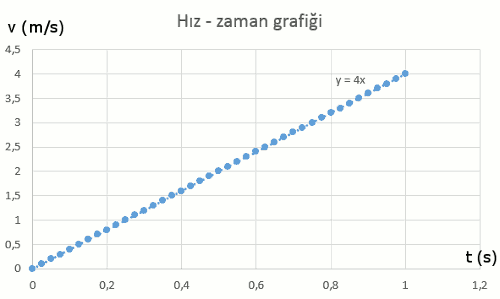
Bu grafiğe doğrusal bir eğilim çizgisi oturtunca y = 4x denklemi çıktı. Şimdi bu ne demek biraz düşünelim. Eğer grafiğin düz bir doğru olduğunu görüyorsak, doğru denklemi yazabiliriz:

y = mx + b

m doğrunun eğimini, b doğrunun y eksenini kestiği noktayı verir. Bu denklemde b = 0, m = 4 çıkmış. Yani doğrunun eğimi 4. Peki birimi ne?

y = v (sürat), ve x = t (zaman)

Yani aslında bu denklem şöyle:

v = 4t

İvmenin tanımını hatırlayın:

a = \frac{\Delta v}{\Delta t}

Öyleyse, hız – zaman grafiğinin eğimi ivmeyi veriyor:

a = \frac{4t}{t} = 4 \space m/s^2

Sabit ivmeli bir hareketlinin herhangi bir andaki hızını şu fomülle bulabiliriz:

v = v_0 + at

Bu soruda v₀ = 0, yani hareketlinin ilk hızı sıfır, harekete başlamadan önce duruyormuş.

Konum zaman grafiği

Hız – zaman grafiği çok kullanışlı bir grafik. Hız – zaman grafiğinin altında kalan alan bize yer değiştirmeyi veriyor. Böylece herhangi bir an için hareketlinin konumunu da hesaplayabiliyoruz. Bu soruda ilk hız sıfır olduğu için her hangi bir andaki yer değiştirme, grafiğin altında kalan üçgenin alanına eşit.

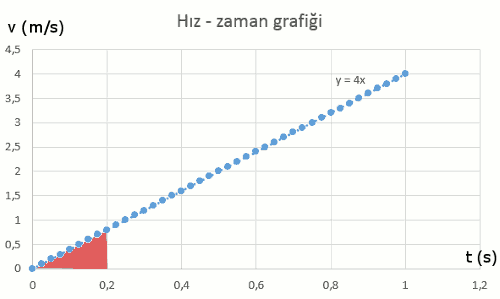
Örneğin, 0 – 0,2 saniye arasında bu hareketlinin aldığı yol yukarıdaki grafikteki kırmızı bölge. Bunu hesaplayabiliriz.

v = v_0 + at v = 0 + 4 \times 0,2 = 0,8 \space m/s \Delta x = \frac{1}{2}(v \times t) \Delta x = \frac{1}{2}(0,8 \space m/s \times 0,2 \space s) = 0,08 \space m

Yani her, zaman veri noktası için, artık konum hesaplayabilirim. Bu hesabı yaptığımda (tabii ki ben yapmıyorum yazıyorum formülü excele o yapıyor) şöyle bir veri tablosu ortaya çıkıyor.

t (s)	x (m)
0	0
0,025	0,00125
0,05	0,005
0,075	0,01125
0,1	0,02
0,125	0,03125
0,15	0,045
0,175	0,06125
0,2	0,08
0,225	0,10125
0,25	0,125
0,275	0,15125
0,3	0,18
0,325	0,21125
0,35	0,245
0,375	0,28125
0,4	0,32
0,425	0,36125
0,45	0,405
0,475	0,45125
0,5	0,5
0,525	0,55125
0,55	0,605
0,575	0,66125
0,6	0,72
0,625	0,78125
0,65	0,845
0,675	0,91125
0,7	0,98
0,725	1,05125
0,75	1,125
0,775	1,20125
0,8	1,28
0,825	1,36125
0,85	1,445
0,875	1,53125
0,9	1,62
0,925	1,71125
0,95	1,805
0,975	1,90125
1	2

Bu veriyi görselleştirmek için hız – zaman grafiğindeki taktiğin aynısını uyguluyorum. Dağılım grafiği çizdiriyorum, yine excele.

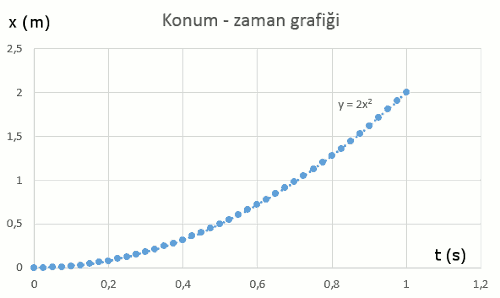
Bu grafiğe ikinci dereceden bir polinom şeklinde bir eğilim çizgisi (model) oturttuğumda bulduğum şey y = 2x². Şimdi bu ne demek:

y = x yani konum, x = t yani zaman, öyleyse bu denklem aslında şöyle:

x = 2t²

Buraya nereden geldiğimizi hatırlayalım. Hız – zaman grafiğinin altındaki alanı hesaplayarak konumu bulduk. Öyleyse, bu 2 yerine ivme cinsinden birşey yazabilir miyiz?

a = \frac{v_{son} - v_{ilk}}{\Delta t}

t = 1 s için:

a = \frac{4 - 0}{1} = 4 \space m/s^2

Bunu en son bulduğumuz konum denkleminde yerine koysak nasıl olur acaba?

x = (\frac{1}{2}4)t^2 = 2t^2

Doğru gibi görünüyor. Genellersek:

x = \frac{1}{2}at^2

Ama dikkat etmemiz gereken iki nokta var. Birincisi ilk hızımız sıfır (v₀ = 0) ve ilk konumumuz da sıfır (x₀ = 0). Eğer bu bilgiyi de eklersek, bir boyutta sabit hızla giden hareketlinin hareket denklemini yazabiliriz. Hareket denklemi konumun zamanın fonksiyonu olarak yazılması anlamına geliyor:

x(t) = x_0 + v_0t + \frac{1}{2}at^2

Bu çok önemli bir denklem, sabit ivmeli hareketi sadece bu denklemi kullanarak anlayabiliriz, yani aslında tüm sorularını çözebiliriz demek.

İvme -zaman grafiği

Son olarak bir de ivme – zaman grafiğine bakalım. Bunun için de excelde grafik çizeceğim. Ama veri tablosunu vermeyeceğim. İvmenin sabit olduğunu zaten biliyoruz. a = 4 m/s² olduğunu bulduk zaten.

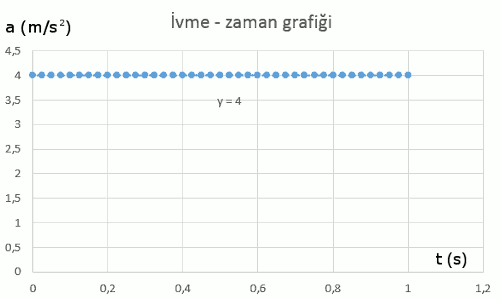
Bu grafikteki y = 4 doğrusu ne demek? y = a yani ivme, öyleyse aslında bu a = 4 m/s² anlamına geliyor. İvme sabit, hareketin her anında 4 m/s² büyüklüğünde ve hep aynı yönde. Çünkü kutu hızlanıyor.

İvme – zaman grafiğinin altında kalan alan bize hız değişimini veriyor. Bunu göstermiyorum, kendiniz yapmayı bir deneyin bakalım.

Düzgün Yavaşlayan Doğrusal Hareket

Aslında düzgün yavaşlayan hareket özel bir durumdan başka bir şey değil. Tekrar veri tablosu ve grafik vermeyeceğim. Bunu da kendiniz çıkarın diyeyim, yapamazsanız bir başka yazıda açıklarız. Ama durumu anlatalım. Eğer bir arabanın sürücüsü, araba giderken frene basarsa ve fren arabaya sabit bir kuvvet uygularsa, araba sabit ivmeyle yavaşlar. Dikkat etmeniz gereken tek şey ivmenin yönü. Hız azaldığı için harekete zıt yönde. Bu nedenle düzgün yavaşlayan bir hareketlinin hareket denklemleri şöyle olur:

x = x_0 + v_0t - \frac{1}{2}at^2 v = v_0 - at

Bu düzgün hızlanan doğrusal harekettekiyle neredeyse aynı, tek fark ivmenin (a) başındaki işaretin eksi olması.

Bir de grafiklerini gösterelim. Hepsinde ilk konumu sıfır ve ilk hızı 4 m/s kabul ediyoruz.

Hız – zaman grafiği şöyle görünüyor:

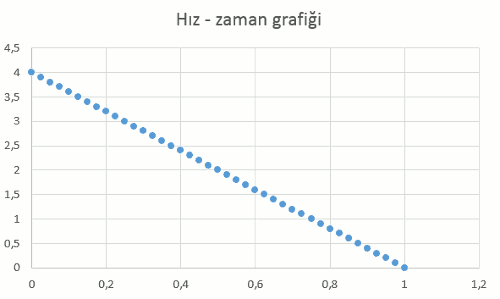
İlk hızı 4 m/s olan hareketlinin 1 saniye sonunda durduğunu görüyoruz hız – zaman grafiğinden.

Konum zaman grafiği de şöyle görünüyor:

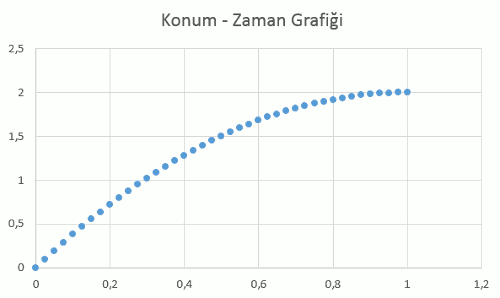
Nihayet, ivme – zaman grafiği de şöyle görünüyor:

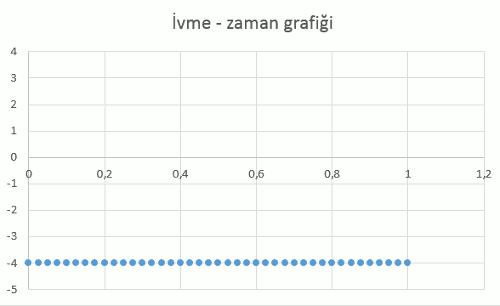
İvme – zaman grafiğinin a = -4 m/s² olduğuna dikkat edin.

Düzgün hızlanan ve yavaşlayan doğrusal hareket ile ilgili kazanımlar

2017 – 11.1.4.1. Bir boyutta sabit ivmeli hareketi örneklerle açıklar.

• Hareket denklemleri verilir.

2017 – 11.1.4.2. Bir boyutta sabit ivmeli hareket ile ilgili hesaplamalar yapar.

• Öğrencilerin sabit ivmeli hareket ile ilgili konum – zaman, hız – zaman ve ivme – zaman grafiklerini yorumlamaları sağlanır.

Düzgün hızlanan ve yavaşlayan doğrusal hareket ile ilgili MEB ve EBA Testleri

• 11. Sınıf Fizik: Bir Boyutta Sabit İvmeli Hareket 1 – Test – 5 (2018) (PDF)
• Cevap anahtarı burada