Elektrik akımının ve voltajın elektrik devrelerinde, devre elemanlarından biri olan direnç ile nasıl etkileştiğini Ohm Kanunu’nda öğrendik. Peki bir devrede birden fazla direnç olursa akım ve potansiyel fark nasıl davranır? Bu yazıda bir elektrik devresinde birden fazla direncin çeşitli şekillerde bağlandığı durumları inceleyeceğiz. Bunu yaparken de birden fazla direncin görevini tek başına yerine getirdiğini düşündüğümüz, gerçekte fiziksel olarak var olmayan, ama matematiksel olarak çok iyi çalışan eşdeğer direnç kavramını kullanacağız.
Dirençlerde seri bağlama ve eşdeğer direnç
Bir uçtan bir uca sıralanmış, aralarında düğüm noktası (kavşak) bulunmayacak şekilde dizilmiş dirençlere seri bağlı veya seri bağlanmış dirençler denir. Seri bağlı dirençlerde birinci direncin bittiği nokta ikinci direncin başladığı noktaya bağlıdır. Kirchoff Kanunları’ndan bildiğimiz gibi eğer devrede bir düğüm noktası yoksa akım korunur, yani devrenin üstündeki akım her noktada aynıdır. Dolayısıyla seri bağlanmış dirençlerin her birinin üstündeki akımın değeri aynı olmak zorundadır. Seri bağlanmış dirençlerin toplam potansiyel farkı da, tüm dirençlerin teker teker potansiyel farklarının toplamına eşittir.
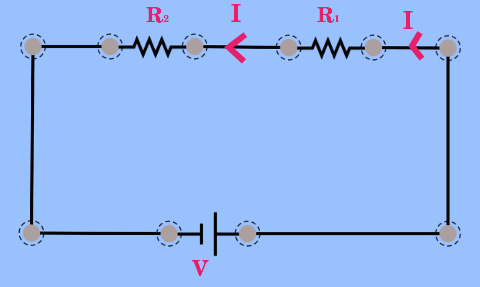
Yukarıdaki resimde iki direnç, R1 ve R2, seri bağlanmış. Pilin sağladığı potansiyel fark devreden bir akım geçmesine neden oluyor. Bu akımın değeri her iki direnç için de aynı. Çünkü akım tek koldan gidiyor, düğüm noktası olmadığı için dağılmıyor. Ama potansiyel fark iki direnç arasında paylaşılıyor. Bu nedenle iki direncin potansiyel farkları toplamı:
∆Veşdeğer = ∆V1 + ∆V2
∆Veşdeğer = IR1 + IR2
∆Veşdeğer = I(R1 + R2)
∆Veşdeğer / I = (R1 + R2)
Reşdeğer = R1 + R2
Buradan seri bağlı iki direncin aslında tek bir direnç gibi davrandığını görüyoruz, buna da eşdeğer direnç diyoruz. Seri bağlı dirençlerde eşdeğer direncin dirençlerin toplamına eşit olduğunu görüyoruz.
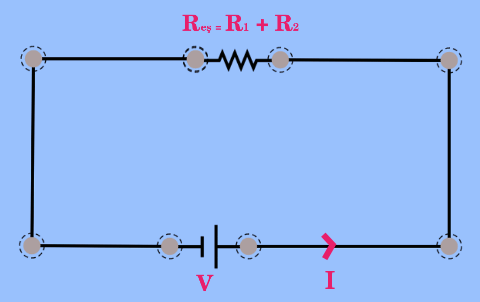
Yukarıdaki resimde dirençlerin seri bağlanması durumunda Reşdeğer = R1 + R2 olduğu görülüyor.
Genellersek, seri bağlı dirençler için eşdeğer direnç formülü:
R_{esdeger} = R_1 + R_2 + .. + R_NTekrar hatırlatalım, devre analizinde dirençlerin seri bağlanmasındaki ana fikir, seri bağlı tüm dirençlerden aynı akımın geçiyor olmasıdır.
Pil bir devreye değişmeyen bir elektromotor kuvvet – emk (voltaj, gerilim veya potansiyel fark) sağlar. Ama değişmeyen (sabit) bir akım sağlamaz. Akımın değeri (büyüklüğü) pilin sağladığı gerilimle birlikte devredeki dirençlere bağlıdır.
Dirençlerde paralel bağlama ve eşdeğer direnç
Eğer birden fazla direnç yan yana hizalanarak bağlanırsa buna paralel bağlama denir. Paralel bağlı dirençlerde birinci ve ikinci direncin hem başlangıç noktaları hem de bitiş noktaları birbirine bağlıdır. Paralel bağlanmış dirençlerin başlangıç noktalarının potansiyeli de bitiş noktalarının potansiyeli de eşittir. Bu nedenle paralel bağlı dirençlerin uçları arasındaki potansiyel fark da aynıdır. Paralel direnç hesaplama aşağıdaki gibi yapılır.
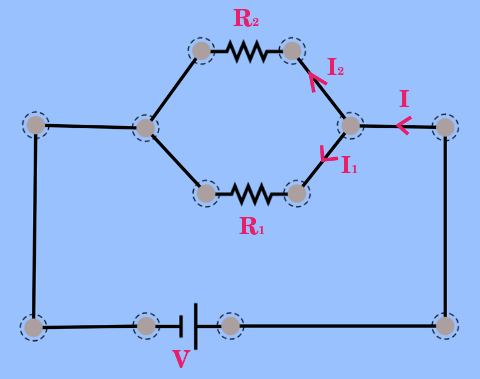
Yukarıdaki resimde paralel bağlanmış iki direnç gösteriliyor. Pilden gelen akım (I) düğüm noktasında Kirchoff’un akımlar kanununa göre iki kola ayrılıyor ( I1 ve I2).
I = I1 + I2
Her iki direnç için Ohm Kanunu’nu uygulayabiliriz. Her iki direncin de potansiyel farkının eşit olduğunu biliyoruz.
Eşdeğer direncin iki direncin görevini tek başına yerine getirebilen direnç olduğunu biliyoruz. Bu iki direncin yerine tek bir direnç koysaydık ne bulurduk? Ohm kanunu eşdeğer direnç için tekrar uygulayalım.
\Delta V = IR_{esdeger} \frac{I}{\Delta V} = \frac{1}{R_{esdeger}}Şimdi bu bulduğumuz ilişkiyi 1. denklemde yerine koyalım:
\frac{1}{R_{esdeger}}= \frac{1}{R_1} + \frac{1}{R_2}Paralel bağlı dirençlerdeki eşdeğer direncin formülü:
R_{esdeger} = (\frac{1}{R_1}+\frac{1}{R_2})^{-1} R_{esdeger} = \frac{R_1 R_2}{R_1+R_2}Aşağıdaki resimde paralel bağlı iki direncin görevini yerine getiren eşdeğer direnç gösteriliyor.
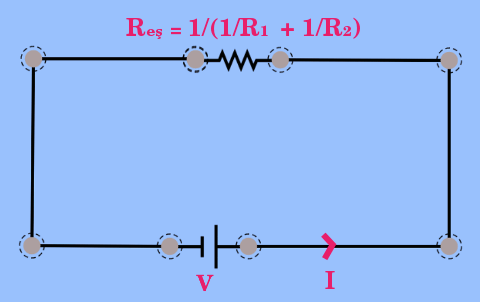
Genellersek, paralel bağlanmış dirençler için eşdeğer direnç formülü:
R_{esdeger} = (\frac{1}{R_1}+\frac{1}{R_2}+..+\frac{1}{R_N})^{-1}Bir kez daha hatırlatalım, devre analizinde dirençlerin paralel bağlanmasındaki ana fikir, paralel bağlı tüm dirençlerin uçları arasındaki potansiyel farkın aynı olmasıdır.
Paralel bağlı dirençlerin eşdeğer direncini bulurken 1/Resdeğer elde ettikten sonra ters çevirmeyi unutmamalısınız.
Eşdeğer direnç, seri ve paralel bağlama örnek soru
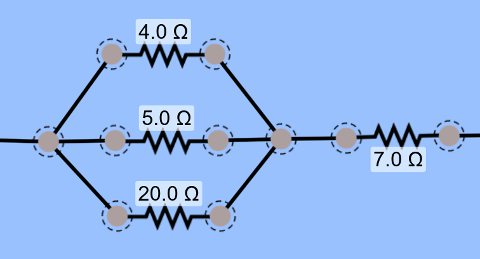
Yukarıdaki şekilde gösterilen elektrik devresinin eşdeğer direnci kaç ohmdur?
Çözüm:
Soru bize paralel bağlanmış üç direncin (4, 5 ve 20 ohm), 7 ohmluk bir dirence seri bağlandığını gösteriyor. Bu soruyu çözmek için böl parçala feth et yöntemini kullanacağız. Önce paralel bağlı dirençlerin eşdeğer direncini bulacağız, sonra bunu tek bir direnç olarak kullanıp tüm devrenin eşdeğer direncini hesaplayacağız.
\frac{1}{R_{es-paralel}} = \frac{1}{4} + \frac{1}{5} + \frac{1}{20}Paydaları eşlemek için ilk terimi 5 ile, ikinci terimi 4 ile, üçüncü terimi 1 ile çarpalım:
\frac{1}{R_{es-paralel}} = \frac{5}{20} + \frac{4}{20} + \frac{1}{20} \frac{1}{R_{es-paralel}} = \frac{5+4+1}{20} = \frac{10}{20} = \frac{1}{2}Şimdi paralel dirençlerin eşdeğer direncini bulmak için bu kesri ters çevirmeliyiz:
R_{es-paralel} = \frac{2}{1} = 2 \space \OmegaDikkat edin, eşdeğer direnç paralel bağlı tüm dirençlerden daha küçük çıktı.
Artık bulduğumuz paralel devrenin eşdeğer direncini tek bir direnç olarak son dirence seri bağlı gibi düşünüp tüm devrenin eşdeğer direncini bulabiliriz.
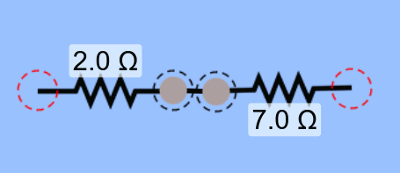
Sorularda verilen devreler size başlangıçta karmaşık görünebilir. Ama unutmamanız gereken dirençler bir devrede ya seri bağlanır ya da paralel bağlanır. Bütün yapmanız gereken hangi dirençlerin seri, hangilerinin paralel bağlandığını belirlemektir. Sonra böl parçala yöntemiyle parçaların eşdeğer dirençlerini bulur ve sonra da tüm devrenin eşdeğer direncini bulursunuz.
Eşdeğer direnç video
Eşdeğer direnç, seri bağlama ve paralel bağlama ile ilgili kazanımlar
2017 – 10.1.2.1. Elektrik akımı, direnç ve potansiyel farkı arasındaki ilişkiyi analiz eder.
- Elektrik devrelerinde eşdeğer direnç, direnç, potansiyel farkı ve elektrik akımı ile ilgili hesaplamalar yapılması sağlanır.
Merhabalar,
Yazıda “seri bağlama”da geçen şu cümlede bir yanlışlık olabilir mi acaba?
“Pilin sağladığı potansiyel fark ile devreden geçen akımın değeri her iki direnç için de aynı”.
Potansiyel fark aynı ise,
∆Veşdeğer = ∆V1 + ∆V2
Bu formülde ∆V1 = ∆V2 olur.
Kafa karışıklığı oluştu. İzah ederseniz çok mutlu olurum. İyi çalışmalar.
Haklısın Yusuf, okuyunca sanki seri bağlamada potansiyel fark da her iki direnç için aynıymış anlamı çıkıyordu. Düzelttim. Şöyle: “Pilin sağladığı potansiyel fark devreden bir akım geçmesine neden oluyor. Bu akımın değeri her iki direnç için de aynı. Çünkü akım tek koldan gidiyor, düğüm noktası olmadığı için dağılmıyor. Ama potansiyel fark iki direnç arasında paylaşılıyor.” Tekrar bir bak, aklına yatmayan başka bir şey daha olursa yorum yaz tekrar bakarım.
Teşekkür ediyorum, çok hızlı ve açıklayıcı bir cevap oldu. Genel olarak paylaşımlarınızı da çok beğendiğimi ifade edeyim.
Beğenmene sevindim. Başka net olmayan bir şeyler yakalarsan yorum yaz, netleştirelim.
Arkadaşlar topraklama çubuğu direnci Rç:2,98 çevre topraklama iletkeni direnci Ri:1,18 temel topraklama iletkeni direnci Rt:1,35 Reş? ne olur formül olarak yazabilirmisiniz
Reş = (R1+R2)/(R1*R2) paralel devre eşdeğer direç ifadesi hatalı olmuş
Çok iyi yakalamışsınız, teşekkürler. Düzeltildi.
ÜÇ PARALEL DİRENÇ OLURSA Reş RORMÜLÜ NE OLURDU
1/Reş = 1/R1 + 1/R2 + 1/R3 olurdu.
Teşekkürler gerçekten çok yararlı oldu
Teşşekür Ederim çok faydalı oldu güzel paylaşım emeğinize sağlık…
Teşekkürler, oldukça yardımcı oldu.
Teşekkürler gerçekten çok faydalı oldu performans ödevi için
Kardeşim iki tanesini çarpıp toplamına bölüyosun çıkan sonuçla son dirençle aynı işlemi yapıyosun
Örneğin 10, 20,5. 1.direnç.2.direnç
________________
10.20 = 200. 1.d+2.d
10+20=30
200/30=1 direnç umarım yardım
edebilmişimdir
Dirençler devreye seri bağlanırsa mi yada paralel bağlanırsa mi fazla akım çeker yani akımı düşürmek için nasıl bir baglanti yapilmali
Aynı potansiyel fark için yüksek direnç, düşük akıma neden olur. Dirençler seri bağlanırsa eş değer direnç değeri yüksek olur.