Hooke Yasası nedir? Örnek sorular ve çözümleri

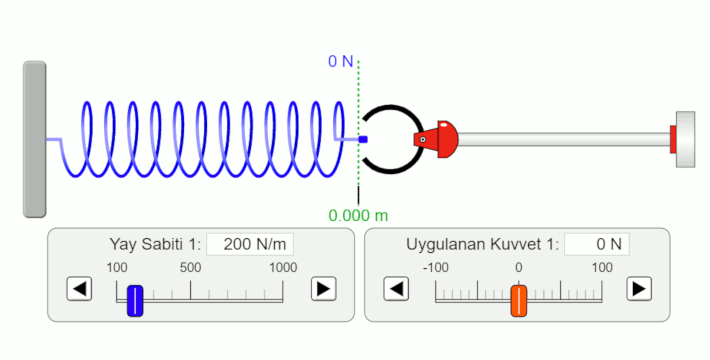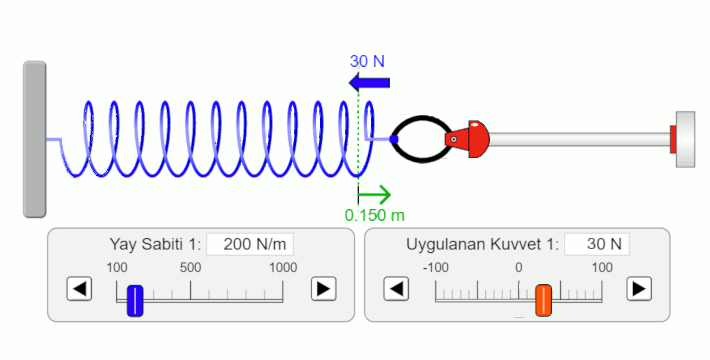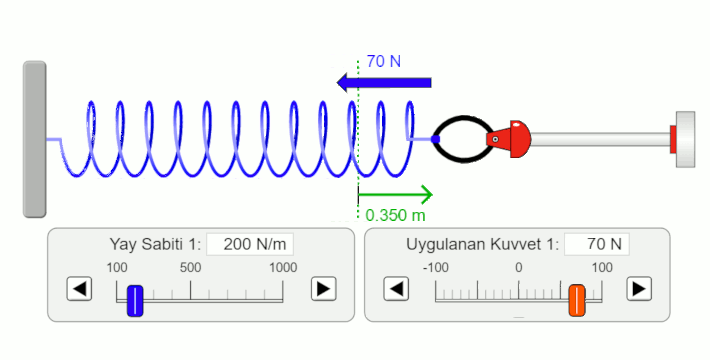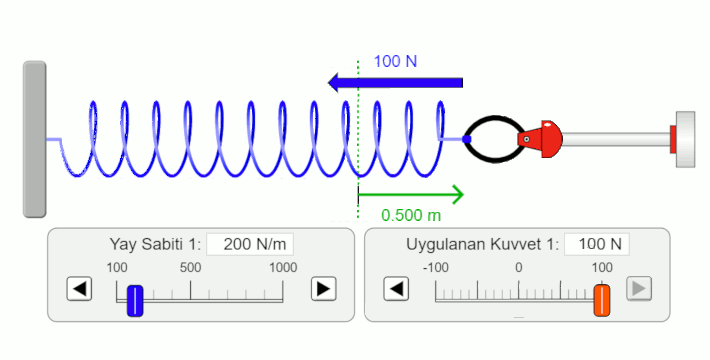
Bu yazıda Robert Hooke’un adının verildiği kuvvet ve esneme miktarı arasındaki ilişki olan Hooke Yasası’nı inceleyeceğiz. Hooke yasası yay gibi esnek cisimlerle ilgilidir. Biz özellikle esnek yaylarla ilgileneceğiz. Yay gibi esnek cisimler üzerlerine kuvvet uygulandığında uzar, sonra serbest bırakıldığında tekrar denge durumuna döner. Yayın ilk konumuna dönmesinin nedeni geri çağırıcı kuvvettir. Bir yayın esnedikten sonra tekrar ilk haline dönebildiği aralığa esneklik sınırı denir. Eğer yaya esneklik sınırından fazla kuvvet uygularsanız yay bozulur, esneklik özelliğini kaybeder. Şimdi yayın sıkıştırılması ya da gerilmesi durumunda yayın esneme uzunluğu ile geri çağırıcı kuvvet arasındaki ilişkiyi inceleyelim. Aşağıdaki resimde yayın gerildiği durumu görüyoruz.

Gözlemlerimizi sıralayalım:

• Yaya uygulanan kuvvetle (siyah halkayla) yayı geriyoruz. Yayın geri çağrıcı kuvvetinin büyüklüğü yaya uyguladığımız kuvvetin büyüklüğüne eşit ve zıt yönlü.
• Yayın uzama miktarı kuvvet arttıkça artıyor. Yayın uzama miktarının vektör olduğunu yani yönünün olduğuna dikkat edin.
• Geri çağırıcı kuvvetin yönü ile yayın uzama yönü birbirine zıt.

Yayın uzama miktarı ile geri çağrıcı kuvvet arasında bir ilişki var mı? Bunun için zaten simülasyonda bir sanal deney yapmış olduk. Tek yapmamız gereken verilerimizi analiz etmek. Yani önce bir tabloya yerleştirmek, sonra da grafiğini çizmek. Tabloda geri çağırıcı kuvvetin işaretinin eksi olmasının nedeni kuvvetin -x yönünde uygulanıyor olması.

F (N)	x (m)
0	0
-10	0.05
-20	0.1
-30	0.15
-40	0.2
-50	0.25
-60	0.3
-70	0.35
-80	0.4
-90	0.45
-100	0.5

Şimdi grafiğine bakalım.

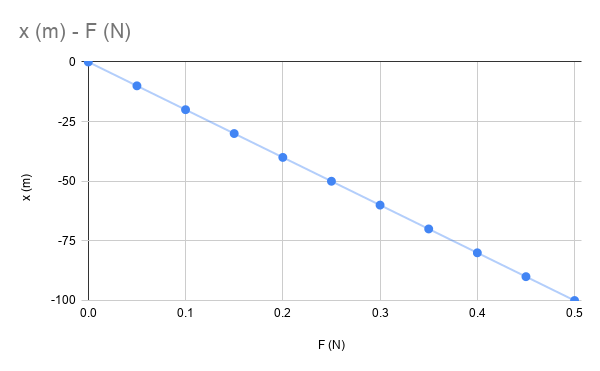
Simülasyondan değerleri aldığımız için grafik fazla mükemmel, hata yok, olsun. (F,x) değerlerinin ip gibi bir düz çizginin üzerinde dizildiğini görüyoruz. Bu çizginin eğimini hesaplarsak geri çağırıcı kuvvet ile uzama miktarı arasındaki ilişkiyi bulmuş oluruz.

k = \frac{F}{x}
Bu durum için iki nokta seçelim, (-80,0.4) ve (-60,0.3) olsun bu noktalar. Öyleyse eğim:
k = \frac{-80-(-60)}{0.4-0.3}=\frac{-20 N}{0.1m}= -200 N/m
Eğimin eksi çıkmasının nedeni geri çağırıcı kuvvetle yayın uzama miktarının zıt yönlü olması. Burada eğimi artı işaretli olarak fiziksel bir büyüklük olarak tanımlıyoruz: Yay sabiti k. Yay sabitinin biriminin N/m olduğuna dikkat edin. Yayı bir metre uzatmak için kaç newton kuvvet uygulanması gerektiği anlamına geliyor.

Artık yay sabitini kullanarak Hooke kanunu tanımlayabiliriz:

F = -kx

Yani, esnek bir yay x kadar sıkıştırıldığında veya x kadar gerildiğinde yaydaki geri çağırıcı kuvvet F_yay= -kx olarak ifade edilir. Bu ilişkiye Hooke Kanunu (ya da yasası) denir. Eksi işareti yayın geri çağırıcı kuvveti ile yaydaki uzamanın (veya kısalmanın) yönlerinin zıt olduğunu anlatır.

Yay sabitinin yayın cinsine göre değiştiğini de söylemeliyim. Tükenmez kalemin içindeki incecik yayla, arabaların amortisörlerinin içindeki kalın yayın yay sabiti farklıdır. Hangisi daha büyüktür? Yorumlarda cevabınızı bekliyorum. Yay sabiti büyük olan yaylara sert yay; küçük olanlara yumuşak yay denir.

Hooke Yasası Örnek Soru

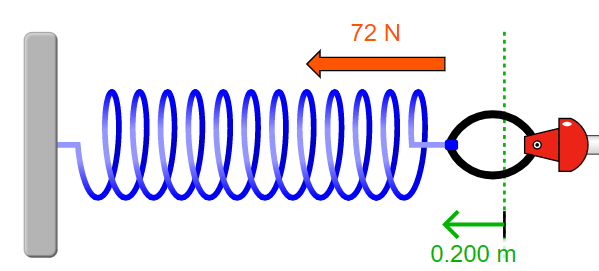
Yukarıdaki şekilde gösterilen yay kırmızı ok yönünde 72 N kuvvet uygulanarak 0.2 m sıkıştırılmıştır. Buna göre (a) yayın geri çağırıcı kuvvetinin büyüklüğü ve yönü nedir? (b) Yay sabitinin değeri nedir?

Çözüm

(a) Yazıda yayın gerildiği durumu incelemiştik. Bu soruda sıkıştırıldığı duruma bakıyoruz. Geri çağırıcı kuvvetin uygulanan kuvvete zıt yönlü ve aynı büyüklükte olduğunu görmüştük. Öyleyse, geri çağırıcı kuvvet +x yönünde ve 72 N büyüklüğündedir.

(b) Hooke yasasını yazalım: F = -kx. Sonra değerleri yerine yerleştirelim:

72 = -k(-0.2) (Neden uzama miktarının önüne eksi işareti koyduk? Çünkü uzama -x yönünde.)

72 = k(0.2)

k = 72/0.2 = 360 N/m

Yayların Seri Bağlanması

Tek yayda Hooke yasasını artık biliyoruz. Peki iki yayı uç uca eklersek ne olur? Aşağıdaki resimde bu durumu görüyoruz, buna yayların seri bağlanması deniyor.

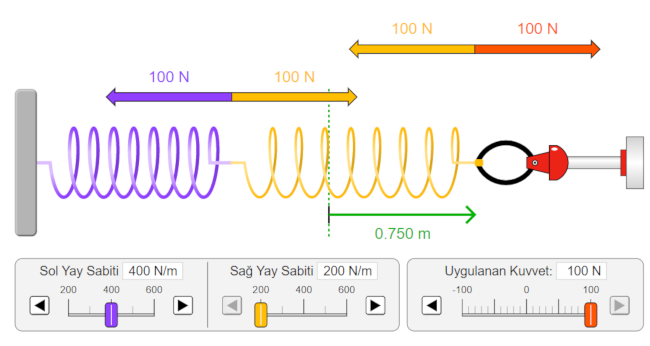
Resmi dikkatlice inceleyelim. Sağdan siyah halka ile 100 N kuvvet uygulanmış. Sağdaki sarı yayın geri çağırıcı kuvveti uygulanan kuvvete (kırmızı) eşit ve zıt yönlü. Soldaki mor yayı sarı yay sağa doğru 100 N kuvvetle geriyor. Mor yayın geri çağırıcı kuvveti buna zıt yönde ve eşit. Burada çok dikkat etmeniz gereken nokta her iki yaya uygulanan kuvvetin eşit olduğu. Sarı yay, kuvveti mor yaya aktarıyor. Yayların toplam uzama miktarı 0.75 m, mor yayın yay sabiti 400 N/m ve sarı yayın yay sabiti 200 N/m.

Şimdi bu özel durumu genelleyelim. Seri bağlanmış iki yayı tek bir yay gibi modelleyelim, bu yaya eşdeğer yay ve yay sabitine k_eş diyelim, toplam uzama miktarı da x_eş olsun.

x_eş = x₁ + x₂

F = F_eş = F₁ = F₂

F_eş = -k_eşx_eş

Şimdi biraz denklemle oynayalım.
-\frac{F_{eş}}{k_{eş}}=x_{eş}
-\frac{F_{eş}}{k_{eş}}=x_1+x_2
x_1 = -\frac{F_1}{k_1};x_2 = -\frac{F_2}{k_2};
-\frac{F_{eş}}{k_{eş}}= (-\frac{F_1}{k_1}) + (-\frac{F_2}{k_2})
F_{eş} = F_1 = F_2 = F
\frac{F}{k_{eş}}= \frac{F}{k_1} + \frac{F}{k_2}

F’ler sadeleştirildiğinde:
\frac{1}{k_{eş}}= \frac{1}{k_1} + \frac{1}{k_2}

Seri Bağlı Yaylar Örnek Soru

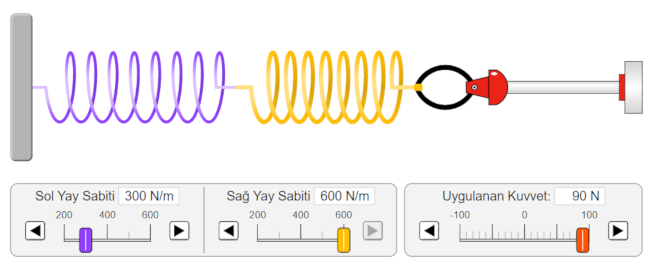
Yukarıdaki şekilde gösterilen iki yay uç uca bağlanmıştır. Soldaki yayın yay sabiti 300 N/m, sağdaki yayın yay sabiti 600 N/m ve soldaki yaya uygulanan kuvvet 90 N’dur. Buna göre:

(a) İki yayın eşdeğer yay sabiti kaç N/m’dir?

(b) Sağdaki ve soldaki yayların uzama miktarları kaç m’dir?

Çözüm

(a) Eşdeğer yay sabitinin formülünü yukarıda çıkardık. Tek yapmamız gereken değerleri yerlerine yerleştirmek:
\frac{1}{k_{eş}}= \frac{1}{k_1} + \frac{1}{k_2}
\frac{1}{k_{eş}}= \frac{1}{300} + \frac{1}{600}=\frac{2}{600} + \frac{1}{600} = \frac{3}{600} = \frac{1}{200}
k_{eş} = 200 \space N/m

(b) Kuvvetlerin aynı olduğunu biliyoruz. Öyleyse:

F₁ = F₂ = 90 N

Soldaki yay için:

90 = 300x₁

x₁ = 90 /300 = 0.3 m

Sağdaki yay için:

90 = 600x₂

x₂ = 90 /600 = 0.15 m

Yayların Paralel Bağlanması

Hooke yasası iki yayı yanyana eklediğimizde nasıl olur? Şimdi cevabını arayacağımız soru bu. Aşağıdaki resimde bu durum gösteriliyor.

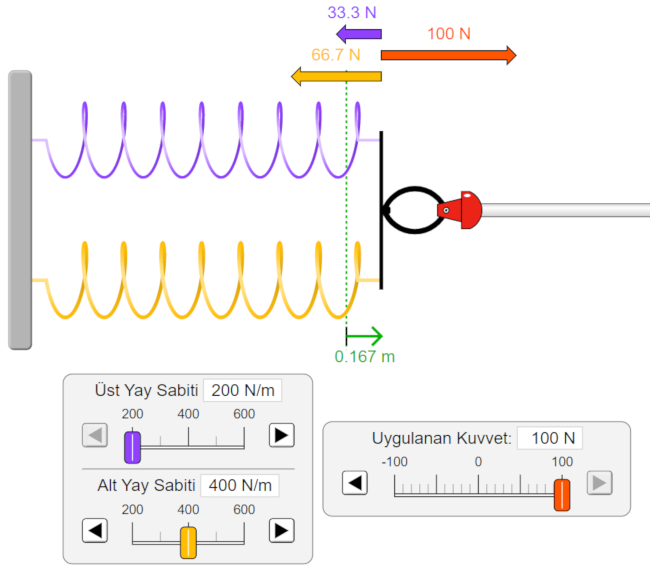
Resmi inceleyelim. Üstteki yayın yay sabitinin 200 N/m, alttaki yayın ise 400 N/m olduğunu görüyoruz. Sağa doğru her iki yaya aynı anda 100 N’luk bir kuvvet uygulanmış. Bu kuvveti dengelemek için üstteki mor yay 33.3 N, alttaki sarı yay 66.7 N geri çağırıcı kuvvet uygulamış. Bu farkın nedeni her iki yayın uzama miktarlarının aynı olması, bu çok önemli.

Şimdi tıpkı seri bağlı yaylarda yaptığımız gibi bu iki yayı tek bir yaymış gibi düşünelim, bu yayın yay sabitine de eşdeğer yay sabiti diyelim. Her iki yayın uzama miktarının, eşdeğer yayın uzama miktarına eşit olduğunu görüyoruz:

x_eş = x₁ = x₂ = x

Uygulanan toplam kuvvetin üstteki ve alttaki yayın geri çağırıcı kuvvetleri toplamına eşit olduğunu da görüyoruz:

F_eş = F₁ + F₂

-k_eşx = -k₁x + (-k₂x)

k_eş = k₁ + k₂

Eşdeğer yay sabitinin iki yayın yay sabitlerinin toplamı olduğunu bulmuş olduk.

Paralel Bağlı Yaylar Örnek Soru

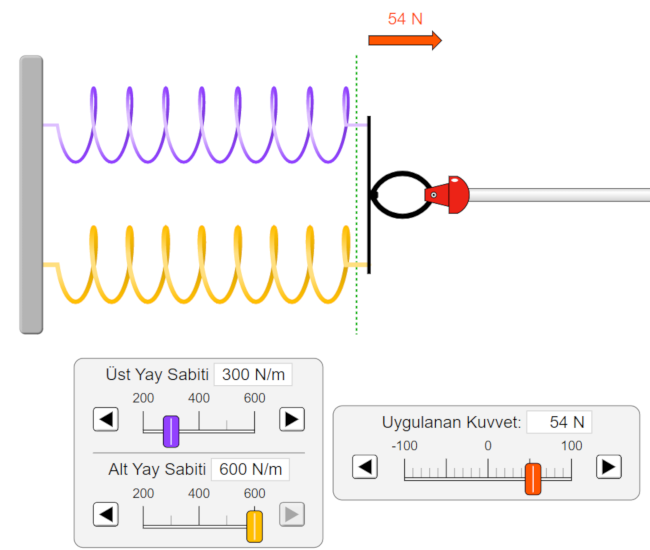
Yukarıdaki şekilde gösterilen iki yay yanyana bağlanmıştır. Üstteki yayın yay sabiti 300 N/m, alttaki yayın yay sabiti 600 N/m ve yaylara uygulanan kuvvet 54 N’dur. Buna göre:

(a) İki yayın eşdeğer yay sabiti kaç N/m’dir?

(b) Yayların uzama miktarları kaç m’dir?

Çözüm

(a) Bu iki yayın paralel bağlandığını görüyoruz. Öyleyse:

k_eş = k₁ + k₂

k_eş = 300 + 600 = 900 N/m

(b) Paralel bağlı oldukları için yayların uzama miktarları birbirine eşit olmak zorunda. Bunu da eşdeğer yay modelinden bulabiliriz.

F = k_eşx

54 = 900x

x = 0.06 m (x₁ = x₂ = x)

Hooke yasası ile ilgili simülasyon

PHET Hooke kanunu simülasyonunu denemenizi öneriyorum.

Hooke yasası ile ilgili kazanımlar

2018 – 11.1.6.1. Yapılan iş ile enerji arasındaki ilişkiyi analiz eder.

• Hooke Yasası verilir.
• Matematiksel hesaplamalar yapılması sağlanır.