Kepler kanunları ya da tam adıyla Kepler’in gezegensel hareket yasaları gezegenlerin Güneş’in etrafındaki hareketlerini açıklar. Kepler, yasalarını Tycho Brahe’nin topladığı gezegenlerin konum verilerini inceleyerek elde etmiştir. Şimdi bu üç kanunu inceleyelim.
Birinci Kanun: Yörüngelerin Şekli Elipstir
Copernicus gezegenlerin yörüngelerinin çember şeklinde olduğunu öne sürmüştü. Kepler gezegenlerin konum verilerinin çember şeklinde yörüngelere değil elips şeklindeki yörüngelere iyi uyduğunu buldu. Aşağıdaki resimde Mars gezegeninin yörüngesi görünüyor.
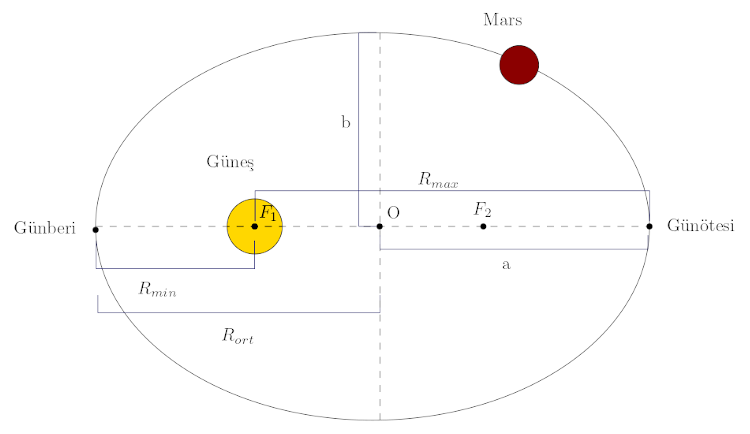
Önce şekli inceleyelim. Elips, basık bir çembere benziyor, iki ekseni var birine büyük eksen diğerine küçük eksen deniyor. İki eksen O noktasında kesişiyor. Şekilde a ile gösterilen uzunluğa yarı-büyük eksen, b ile gösterilen uzunluğa yarı-küçük eksen deniyor. Elipsin iki adet odak noktası var, F1 ve F2 ile gösteriliyor. Şimdi yörüngeyi yorumlayalım. Öncelikle Güneş elipsin odaklarının birinde. Mars’ın Güneş’e en yakın olduğu noktaya günberi, en uzak olduğu noktaya günötesi deniyor. Güneş ile Mars arasındaki uzaklık en az günberide (Rmin), en fazla da günötesinde (Rmax) oluyor. Bu iki uzaklığın ortalaması da:
R_{ort} = \frac{R_{min}+R_{max}}{2} = a
Kepler’in iddiası sadece Mars’ın değil, tüm gezegenlerinin elips şeklinde yörüngelerde dolandığı. Diğer iki kanun da buradan geliyor.
İkinci Kanun: Eşit Sürede Eşit Alanlar Taranır
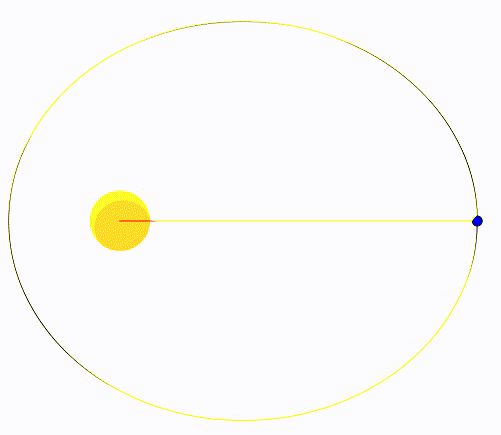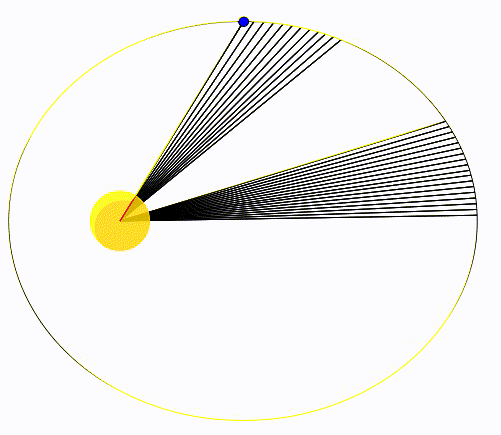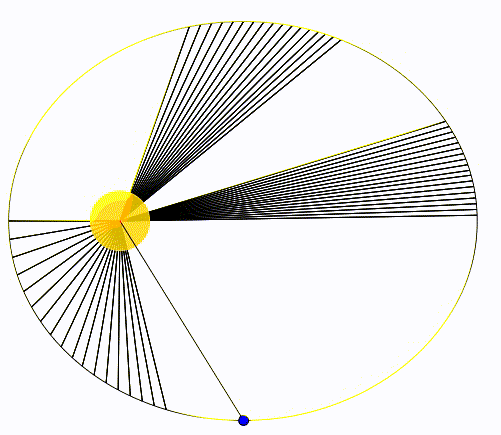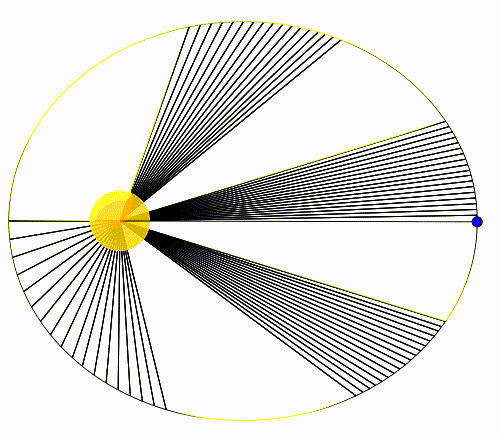
Kepler’in ikinci yasası Güneş ve gezegen arasındaki çizginin, gezegenin hareketi boyunca eşit zaman aralıklarında, eşit alanlar taradığını söyler. Bunu önce bir animasyonla gösterelim. Aşağıdaki animasyonda bir gezegen Güneş’in etrafında dolanıyor. Hareketi esnasında gezegen ve Güneş arasındaki çizgi eşit sürelerde iz bırakıyor ve elipste bir alan tarıyor. Dikkatimizi çeken iki özellik var. İlki gezegen Güneş’ten uzaktayken, özellikle günötesindeyken, görece yavaş hareket ediyor, hızı düşük. Ama Güneş’e yaklaştıkça, özellikle günberideyken, hızlı hareket ediyor. Bu bizi ikinci özelliğe götürüyor, siyah çizgilerin yoğunluğuna bakın, uzaktayken sıklar yakındayken seyrekler. Eğer hesaplarsak eşit sürede taranan alanların birbirine eşit olduğunu görüyoruz. Keplerin ikinci kanunun fiziksel nedeni de açısal momentumun korunumudur.
Üçüncü Kanun: Yarıçapın Küpünün Periyodun Karesine Oranı Sabittir
Kepler, gözlem verilerini kullanarak üçüncü kanununa ulaşmış. Buna göre gezegenlerin tümü için ortalama yarıçapın (Rort) küpünün (üçüncü kuvvetinin) periyodun karesine (ikinci kuvvetine) eşit olduğu sonucuna varmış.
\frac{R_{ort}^3}{T^2} = sabitBu kanunun fiziksel nedenini de Newton’un evrensel kütle çekim yasası ile açıklayabiliyoruz. Kütle çekim kuvvetinin çembersel harekete neden olan kuvvet olduğunu hatırlatsak, M1 Güneş’in kütlesi, M2 gezegenin kütlesi olmak üzere:
G\frac{M_1 M_2}{R^2} = M_2 \omega^2 R \omega = \frac{2 \pi}{T} G\frac{M_1}{R^3} = (\frac{2 \pi}{T})^2Düzenlersek:
\frac{R^3}{T^2} = \frac{G M_1}{4\pi^2}
Newton’un genellemesi ile Kepler yasaları karşılıklı yerçekimlerinin etkisi altında hareket eden herhangi iki cisme uygulanabilir hale gelir. Örneğin, bu yasalar şu durumlarda da geçerlidir:
- Ay’ın Dünya’nın yörüngesinde dolanması
- Dünya’ının etrafında dolanan yapay uydular
- Birbirinin yörüngesinde dolanan iki yıldız
Kepler kanunları ile ilgili uyarılar
Kepler kanunlarının üçü de iki cisim için geçerlidir, bu cisimlerin birinin kütlesinin çok büyük diğerinin ilkine göre çok küçük olduğu kabul edilir. Ayrıca Pluto (ki cüce gezegen olarak kabul ediliyor) hariç gezegenlerin yörüngelerinin basıklığı (eksantrikliği) çok fazla değildir, odak noktaları genellikle birbirine oldukça yakındır.
Örnek Soru 1
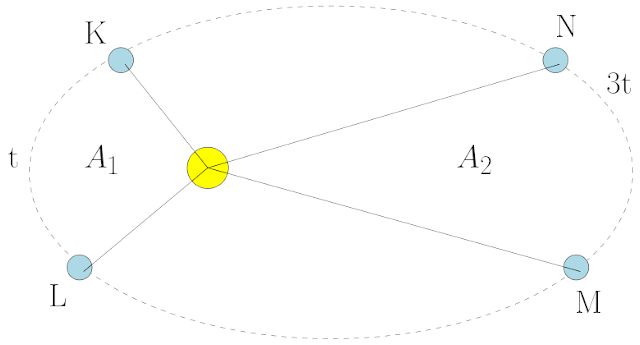
Şekilde Pluto’nun Güneş etrafında dolanması gösterilmiştir. Pluto yörüngesinde K noktasından L noktasına t sürede, M noktasından N noktasına 3t sürede ulaşmıştır. Yarıçap vektörünün K-L arasında taradığı alan A1, M-N arasında taradığı alan A2 ise A1/A2 oranı kaçtır?
Çözüm
Kepler’in ikinci kanunu bize gezegenlerin hareketlerinde eşit sürelerde eşit alanlar taradığını söylüyor. Öyleyse taranan alanın süreye oranı sabit olmalı (hatırlayın açısal momentumun korunumundan geliyor bu):
\frac{A_1}{t} = \frac{A_2}{3t}
Örnek Soru 2
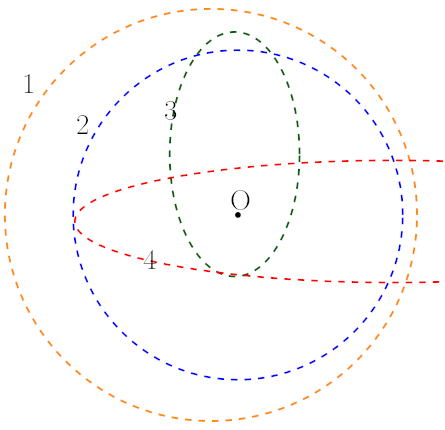
Şekilde O noktasında bulunan bir yıldız gösteriliyor. Bu yıldızın etrafında dolanan gökcisimlerinin yörüngeleri 1,2,3,4 ile gösterilenlerden hangileri gibi olabilir?
Çözüm
Kepler’in birinci kanunu yörüngelerin elips şeklinde olduğunu söylüyor.
- 3 numaralı yörünge bir elips ve odakların birinde yıldız var, bu yörünge mümkün.
- 4 numaralı yörünge de bir elips, o da mümkün.
- 2 numaralı yörünge bir çember, çember elipsin özel bir durumu, çemberin merkezindeyse yıldız o yörünge de olur. Yani 2 de mümkün.
- 1 numaralı yörünge bir çember ama yıldız çemberin merkezinde değil. Dolayısıyla bu yörünge mümkün değil.
Örnek Soru 3
Jüpiter’in uydularından Io ve Europa’nın çembersel yörüngelerde hareket ettiğini kabul edelim. Europa’nın yörünge yarıçapı Io’nunkinin 1,6 katı ise, Europa’nın periyodunun Io’nun periyoduna oranı kaçtır?
Çözüm
Kepler’in üçüncü kanununu kullanalım.
\frac{R_{Europa}^3}{T_{Europa}^2} =\frac{R_{Io}^3}{T_{Io}^2}
Düzenleyelim:
\frac{R_{Europa}^3}{R_{Io}^3} = \frac{T_{Io}^2}{T_{Europa}^2}
Kepler kanunları ile ilgili kazanımlar
12.1.5.1. Kepler Kanunları’nı açıklar.
- Matematiksel hesaplamalara girilmez (biz biraz girdik).
Basit harmonikte ekleyin lütfen
Basit harmonik de*
Hocam anlatımınız için teşekkürler, bunların toplu pdf i var mıdır acaba?