Konum nedir? Hareketi anlamanın ilk şartı

Fizikte konum nedir sorusunun cevabı bir cismin belli bir anda nerede olduğudur. Bir cismin yerini ancak cismin bir referans noktasına göre mesafesi ve yönüyle belirleyebiliriz. Konum vektörel bir büyüklüktür, bu nedenle hem büyüklüğü (uzunluğu) hem de yönü olmak zorundadır. Konumun birimi metre’dir (m), uzunluk birimiyle aynıdır.

Bir Boyutta Konum nedir?

Konumu anlamak için önce en basit durum olan bir boyutta, yani bir doğru üzerinde bir cismin yerini inceleyelim.

Örnek Soru 1 – Yatay doğrultuda konum nedir?

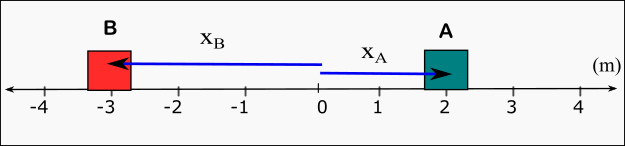
Şekildeki A ve B kutularının 0 ile gösterilen referans noktasına göre konumları nedir?

Çözüm:

Önce referans noktasının düz yolun tam ortasında olduğuna, bu noktanın sağında artı işaretli sayıların solunda eksi işaretli sayıların yazıldığına dikkat etmelisiniz.

Yatay doğrultuda konumu x simgesiyle gösteririz, çünkü x-ekseninden bahsediyoruz.

A kutusunun konumu x_A = +2 m’dir, artı işareti konumun başlangıç noktasının sağında olduğunu gösterir. B kutusunun konumu x_B = -3 m olur, eksi işareti konumunun referans noktasına göre solda olduğunu gösterir.

Örnek Soru 2 – Düşey Doğrultuda Konum nedir?

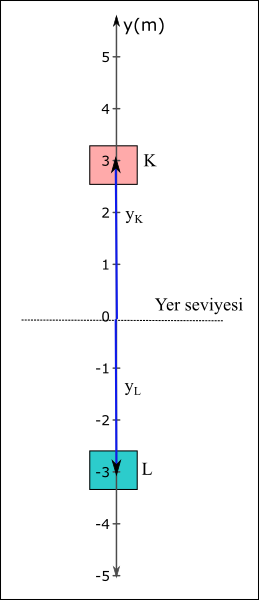
Şekilde K asansörü -1. katta, L asansörü 1. katta durmaktadır. İki kat arasındaki mesafe 3 m olduğuna göre K ve L asansörlerinin yere göre konumları nedir?

Çözüm:

Bu soru da da referans noktası olarak yer seviyesini aldığımıza ve 0 olarak gösterdiğimize dikkat edin. Düşey doğrultuda konumu y simgesiyle gösteririz, çünkü y-eksenini kastediyoruz. y-eksenin 0 noktasına göre yukarı yönünde olan sayıları artı, aşağı yönde olan sayıları eksi işaretiyle gösterdik.

K asansörünün konumu y_K = +3 m’dir, artı işareti konum vektörünün yukarı yönde olduğunu gösterir.

L asansörünün konumu y_L = -3 m olur, eksi işareti konum vektörünün düşeyde aşağı yönü gösterdiği anlamına gelir.

İki Boyutta Konum nedir?

Konum yalnızca bir boyutta belirtilmez, iki boyutta da geçerlidir. Bu durumda konum vektörünün iki bileşeni vardır: hem yatay hem de düşey.

Örnek Soru 3 – Yatay ve düşey dik eksenlerde konum nedir?

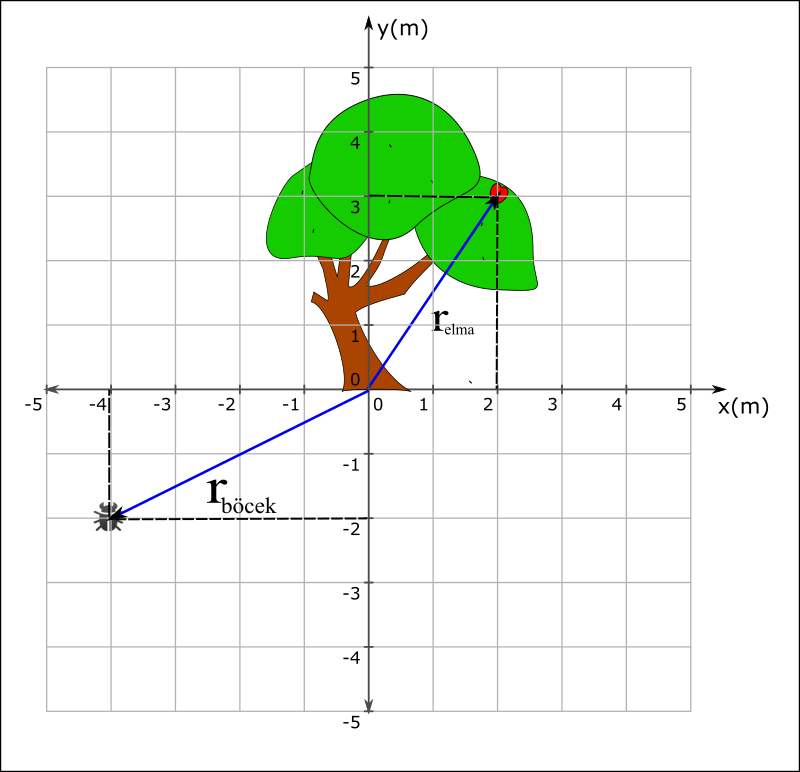
Yukarıdaki şekildeki ağaçtaki elmanın ve toprağın altındaki böceğin konumlarını gösteriniz.

Bir boyutta konumu bir doğru üzerindeki bir sayı ve yönünü gösteren işaretiyle belirleyebiliyorduk. İki boyutta hem yatay (x ekseni) hem de düşey (y ekseni) eksenlerimiz olmak zorunda. Konum vektörünü bu iki eksenin bileşeni olarak ifade edebiliriz.

Konum vektörünü iki boyutta r simgesi ile gösteririz, bu konumun en genel ifade ediliş şeklidir.

\vec{r} = (x, y)

x sayısının işareti x-eksenine göre (sağda ya solda), y’nin işareti y-eksenine göre (yukarıda ya da aşağıda) cismin konumunun yönünü gösterir.

Konum vektörünün şiddetini yani uzunluğunu Pisagor teoreminden buluruz.

r^2 = x^2 + y^2

Konum vektörü üzerinde ok olan \vec{r} ile konum vektörünün büyüklüğü (şiddeti) üzerinde ok olmayan r ile gösterilir.

Şimdi şekilde gösterilen elmanın konum vektörünü yazalım, sonra da uzunluğunu bulalım.

\vec{r}_{elma} = (2 \space m, 3 \space m) {r}_{elma}^2 = 2^2 + 3^2 = 4 + 9 = 13 r_{elma} = \sqrt{13} \space m

Şimdi de böceğin konum vektörünü yazalım ve şiddetini hesaplayalım.
\vec{r}_{bocek} = (-2 \space m, -4 \space m)
{r}_{bocek}^2 = (-2)^2 + (-4)^2 = 4 + 16 = 20
r_{bocek} = \sqrt{20} \space m
r_{bocek} = 2\sqrt{5} \space m

Örnek Soru 4 – Yatay ve yatay dik eksenlerde konum nedir?

Bir otobüs önce kuzey yönünde 30 km, sonra doğu yönünde 40 km yol almıştır. Otobüsün harekete başladığı noktaya göre son konumu nedir?

Çözüm:

İki boyutta konum yalnızca yatay ve düşey doğrultuda olmak zorunda değildir. Kuş bakışı bakıldığında da bir yüzey üstünde iki boyuttan bahsedebiliriz. Bu durumda genellikle coğrafi yönler eksenleri gösterir. Kuzeyi +x yönü, Güneyi -x yönü, Doğuyu +y yönü ve Batıyı -y yönü olarak alırız.

Otobüsün konum vektörü ve konum vektörünün uzunluğu şöyle bulunur:

\vec{r}_{otobus} = (30 \space km, 40 \space km) {r}_{otobus}^2 = 30^2 + 40^2 = 900 + 1600 = 2500 {r}_{otobus} = \sqrt{2500} = 50 \space km

Konum Problemleri

1. Bir helikopter yerden 600 m yükseklikte askıda durmaktadır. Helikopterin konum vektörünü çizin ve şiddetini hesaplayın.
2. Oyuncak bir araba bir masada, masanın sol alt köşesinin 5 cm sağında 12 cm yukarısındadır. Oyuncak arabanın konumunu belirleyiniz. (Hem konum vektörünü çizin hem de konum vektörünün şiddetini hesaplayın).

Konum ile ilgili Fizik Dersi Kazanımları

9.3.1.3. Konum, alınan yol, yer değiştirme, sürat ve hız kavramlarını birbirleri ile ilişkilendirir.

Konum ile ilgili Test

• Hareket Testi: Temel Kavramlar