Kütle merkezinin ve ağırlık merkezinin temel kavramlarını bir önceki yazıda öğrendik. Şimdi örnek soruları çözerek bu kavramların nasıl kullanıldığını göreceğiz.
Örnek soru 1
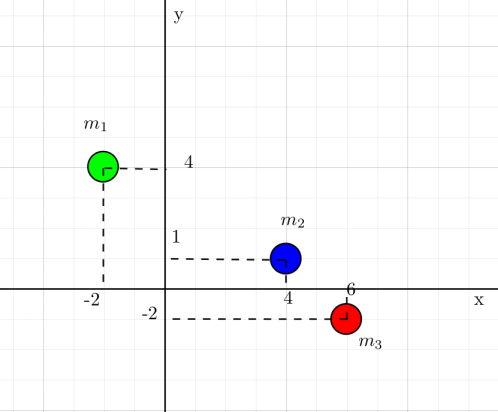
m1 = m, m2 = 2m ve m3 = 3m kütleli cisimler şekildeki koordinat sisteminde gösterildiği gibi yerleştirilmiştir. Buna göre yerçekimi ivmesinin sabit olduğu ortamda bu cisimlerin oluşturduğu sistemin ağırlık merkezinin koordinatları (xKM,yKM) nedir?
Çözüm
Soru bütün kütlelerin (x,y) koordinatlarını vermiş, kütlelerin görece oranlarını da vermiş. Ağırlık merkezi koordinatlarının nasıl bulunduğunu da öğrenmiştik. Yerçekimi ivmesi sabitse ağırlık merkezi ile kütle merkezi aynı noktada oluyordu. Öyleyse denklemleri çözeceğiz:
x_{KM} = \frac{m_1x_1 + m_2x_2 + m_3x_3}{m_1+m_2+m_3}
Şimdi de kütle merkezinin y koordinatını bulalım.
y_{KM} = \frac{m_1y_1 + m_2y_2 + m_3y_3}{m_1+m_2+m_3}
Böylece kütle ve ağırlık merkezinin koordinatlarını (x,y) = (4,0) olarak bulduk.
Örnek soru 2
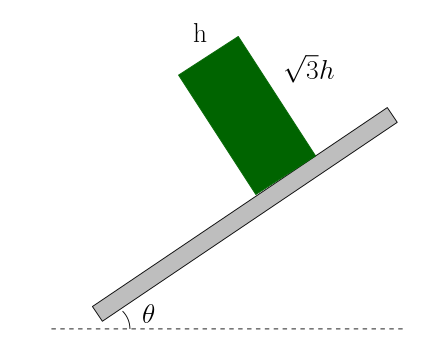
Şekilde gösterilen türdeş cisim bir eğik düzlem üzerine yerleştirilmiştir. Eğik düzlemin açısı cisim devrilinceye kadar artırılmaktadır. Cisim kaç derece açıyı geçince devrilir?
Çözüm
Şekli ağırlık vektörünü ve bileşenlerini gösterecek şekilde tekrar çizelim.
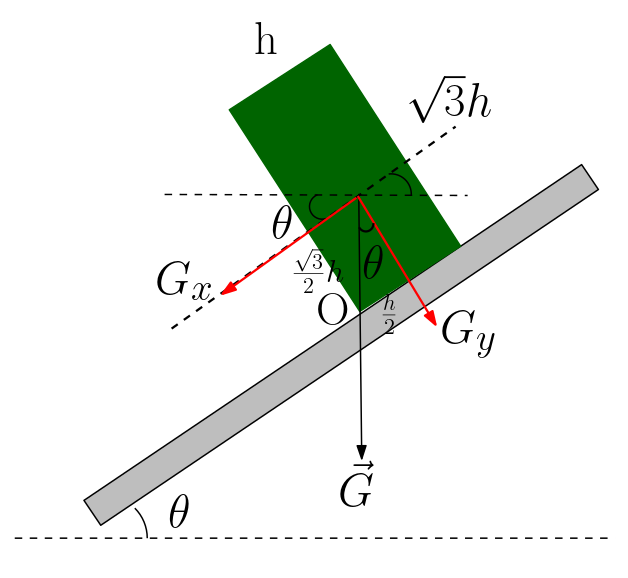
Cismin devrilmesi için gereken şart ağırlık vektörünün uzantısının cismin tabanından öteye geçmesi. Bu durumda ağırlık vektörü tam O noktasına geldiğinde cismin son denge durumu oluşuyor. Açı daha fazla artırılırsa devriliyor. Peki bu açıyı nasıl bulacağız. Cisme torku uygulayan Gx yani ağırlığın x bileşeni ve Gy yani ağırlığın y bileşeni . Uzaklıkları da geometriden bulabiliriz. Ağırlık merkezi cisim bir dikdörtgen olduğu için köşegenlerinin kesişim noktasında. Bu noktada her iki kenarın uzaklıklarının yarısının olduğu noktaya denk geliyor. Şimdi tork denklemini yazalım.
G_x \times \frac{\sqrt{3}}{2}h + (-G_y \times \frac{h}{2}) = 0
Gy için eksi işaretini kullanmamızın nedeni cismi Gx‘e göre zıt yönde çeviriyor olması. Düzenleyelim:
G_x = G sin\theta; \space G_y = G cos\theta
Tanjantı arctanjant fonksiyonuyla bulduk, hesap makinesi kullandık. Yorumlayalım, cisim, eğik düzlem 26 dereceyi geçtiği anda devrilir.
Örnek soru 3

Şekildeki eşit bölmeli türdeş (homojen) çubuğun sağdan dört bölmesi, beşinci ile sekizinci bölmesi üzerine katlanıyor. Buna göre yeni oluşan çubuğun ağırlık merkezi ilk durumdaki ağırlık merkezine göre kaç bölme yer değiştirir?
Çözüm
Önce şekli çizip gözümüzde canlandırmamız lazım.
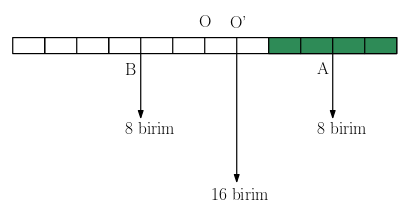
Her bölümün ağırlığına 1 birim dedik (Newton’da diyebilirdik). Sağdan katlanan dört birimi yeşil renkle gösterdik. Üstteki ve alttaki bölmelerle toplam 8 bölme var bu yeşil kısımda. Dolayısıyla bu kısmın ağırlığı 8 birim oldu. Bu 8 birimin ağırlık merkezini yeşil çubuğun orta noktası olan A ile gösterdik.
Beyaz renkle gösterilen bölmeler de 8 tane, onların da ağırlığı 8 birim. Beyaz kısmın ağırlık merkezi de beyaz çubuğun orta noktası olan B noktası. A ile B noktaları arasında 6 bölüm mesafe var. Her iki ucundan da sekizer birim kuvvet etkiyor. Demek ki ağırlık merkezi tam ortada olacak bunu da O’ noktasıyla gösterdik. O ve O’ noktaları arasında 1 bölme mesafe olduğunu görüyoruz.
Örnek soru 4
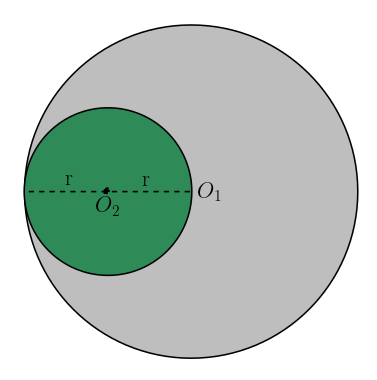
Aynı düzgün ve türdeş alüminyum levhadan r ve 2r yarıçaplı iki daire şeklinde levha kesilip şekildeki gibi yapıştırılıyor. Buna göre oluşan yeni levhanın ağırlık merkezi O1 noktasından kaç r uzaklıkta olur?
Çözüm
Bu soruyu çözmek için yine şeklimizi ağırlık vektörlerini göstererek tekrar çiziyoruz.
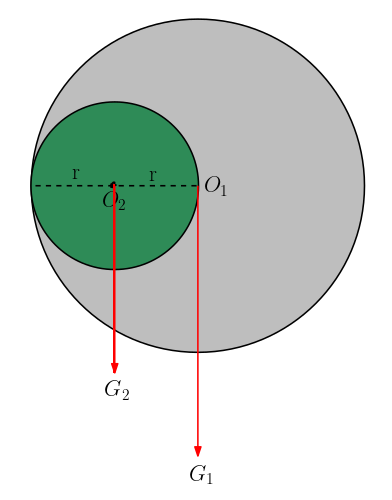
Buradan G1 ve G2 ağırlıklarını hesaplayabiliriz. Kalınlıklarının aynı olduğunu ve türdeş olduklarını biliyoruz. Öyleyse ağırlıklar dairelerin alanlarıyla orantılı.
G_1 = \pi(2r)^2 = 4\pi r^2; \space G_2 = \pi(r)^2
Şimdi oranları biliyoruz. G2 = G dersek G1 = 4G olduğunu görüyoruz. Biraz daha sadeleştirelim çizimimizi.
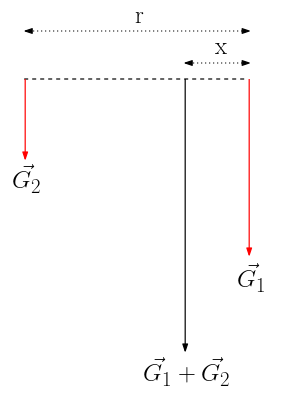
- x büyük dairenin merkezinden birleştirilmiş levhanın ağırlık merkezine uzaklığı.
- r-x küçük dairenin merkezinden yeni ağırlık merkezine uzaklığı.
- Şimdi tork denklemini yazıp bulabiliriz.
Eksi işaretini koymamızın nedeni bu levhaların ağırlık merkezine göre uyguladığı torkların zıt yönlü olması.
4Gx = G(r-x)
Örnek soru 5
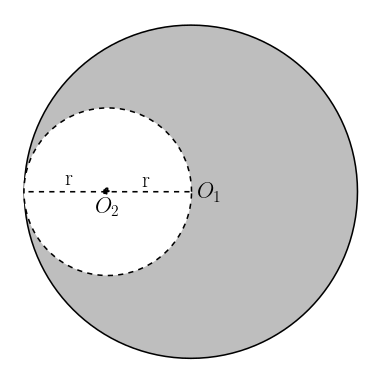
Düzgün ve türdeş alüminyum levhadan önce 2r yarıçaplı bir daire şeklinde bir levha oluşturuluyor. Sonra bu levhadan şekilde görüldüğü gibi r yarıçaplı bir dairesel bölge kesilip çıkarılıyor. Buna göre oluşan yeni levhanın ağırlık merkezi O1 noktasından kaç r uzaklıkta olur?
Çözüm
Öncelikle küçük dairenin (kesilen kısmın) ağırlığı G ise büyük dairenin kesilmeden önce 4G olduğunu görebiliyoruz. Bunu ağırlıklarıın dairelerin alanlarıyla orantılı olmasına dayanarak söylüyoruz.
G_1 = \pi(2r)^2 = 4\pi r^2; \space G_2 = \pi(r)^2
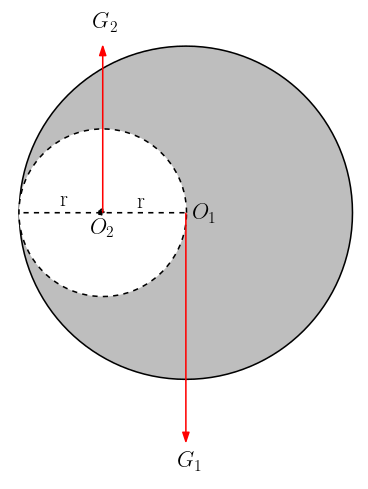
Oluşan paralel ve zıt yönlü kuvvetlerin (yani G1 ve G2‘nin) bileşkesinin uygulama noktası sistemin ağırlık merkezidir. Bileşke kuvvetin büyüklüğü iki kuvvetin farkına, yönü büyük kuvvetin yönüne doğru olacak. Bileşke kuvvetin uygulanma noktası O1 noktasının sağında olmalı. (Bir düşünün yoksa dengede kalabilir mi?)
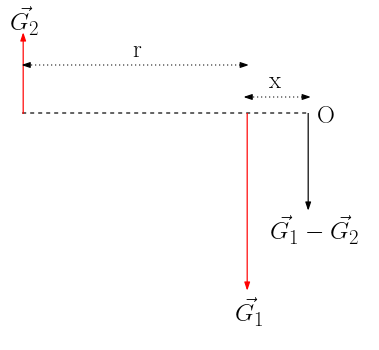
Bileşke kuvvetin O1 noktasına olan uzaklığını x olarak alalım. Şimdi de tork denklemini yazalım:
\vec{G_2} \times (r+x) + (-\vec{G_1 \times x}) = 0
Eksi işaretinin nereden geldiğini anladınız mı? Bu kuvvetler sistemi O noktasına göre zıt yönlere döndürüyorlar.
G(r+x) = 4Gx
Yani levhanın ağırlık merkezi O1 noktasından r/3 kadar sağda olur.
Kütle ve Ağırlık merkezi ile ilgili kazanımlar
11.1.9.3. Kütle merkezi ve ağırlık merkezi ile ilgili hesaplamalar yapar.