Lami teoremi (ya da Stevin bağıntısı), tek bir noktayan etkiyen, aynı düzlemde olan ve kesişen üç dengelenmiş kuvvet arasındaki matematiksel ilişkiyi kolayca bulmamızı sağlayan bir araçtır. Bu cümleyi biraz parçalayalım. Öncelikle kuvvetlerin denge durumunda olması lazım. Kuvvetlerin aynı düzlemde olması lazım. Kuvvetlerin aynı noktaya uygulanması lazım. Bu şartlar sağlandıysa Lami teoremi formülü şöyle diyor: Her kuvvetin büyüklüğünün karşısındaki açının sinüsüne oranı sabit ve birbirine eşit olmak zorunda. Şekille anlamak daha kolay olacak.
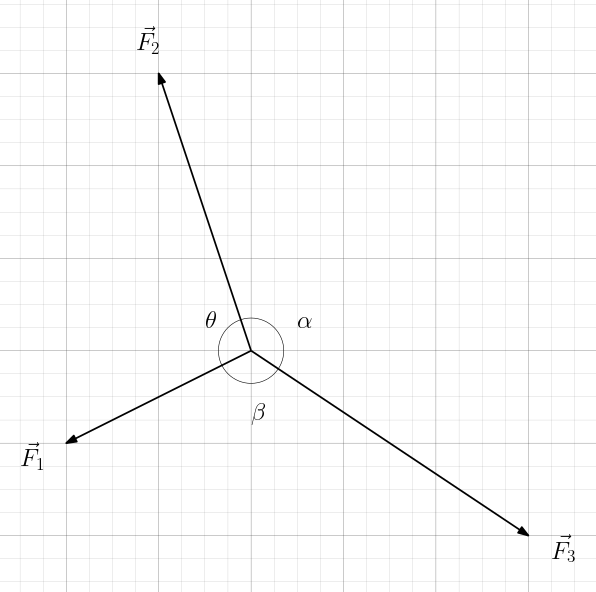
Yukarıdaki şekilde üç kuvvetin aynı noktaya uygulandığını görüyoruz, kuvvetler kesişiyor ve dengelenmiş durumdalar. Bu şekil için Lami teoreminin formülü şöyle: (k sabit bir sayı).
\frac{|\vec{F_1}|}{sin\alpha} = \frac{|\vec{F_2}|}{sin\beta} = \frac{|\vec{F_3}|}{sin\theta} = k
İyi de Lami teoremine ne gerek var diye düşünüyor olabilirsiniz. Kesişen dengelenmiş üç kuvveti bileşenlerine ayırıp bir soruda bize sorulan bilinmeyen kuvveti ya da açıyı bulamaz mıyız? Buluruz elbette, ama bu işlemler uzun sürebilir, bazen de epeyce trigonometri bilgisi gerektirebilir. İşte bu nedenle Lami teoremi bir kısa yol olarak kullanılır.
Örneğin, bu üç açının büyükten küçüğe sıralanışını sorsam? Lami teoremini biliyorsanız, bu soruyu cevaplamak için tek bilmeniz gereken kuvvetlerin büyükten küçüğe sıralanışı. Şekilden bunu görebiliyoruz, kareleri sayarak her kuvvetin büyüklüğünü (şiddetini) bulabiliriz.
|\vec{F_1}| = \sqrt{2^2 + 2^2} = \sqrt{8}
Demek ki:
F3 > F2 > F1
|\vec{F_1}| sin \beta = |\vec{F_2}| sin \alpha
F2 > F1 olduğuna göre eşitliğin korunabilmesi için sinα > sinβ olmalı. Trigonometriden hatırlarsanız (hatırlamadıysanız da şimdi öğreniyorsunuz), sinüsü büyük olan açının kendisi de büyüktür. Yani α > β demek.
|\vec{F_2}| sin \theta = |\vec{F_3}| sin \betaF3 > F2 olduğuna göre yine eşitliğin korunabilmesi için sin β > sin θ olmak zorunda. Sonucumuz β > θ.
Birleştirirsek:
α > β > θ
Şimdi yorumlayalım. En büyük kuvvetin karşısında en küçük, en küçük kuvvetin karşısında en büyük açı var.
Lami Teoreminin İspatı
Peki nereden biliyoruz bu teoremin doğru olduğunu. Türetip görelim. Hatırlayın, bir cismin dengede olabilmesi için cisme uygulanan kuvvetlerin vektörel toplamlarının sıfır olması gerekir. Ayrıca vektörleri de taşıyabiliyoruz. Yukarıdaki şekildeki kuvvetleri bir üçgen biçiminde gösterebiliriz.
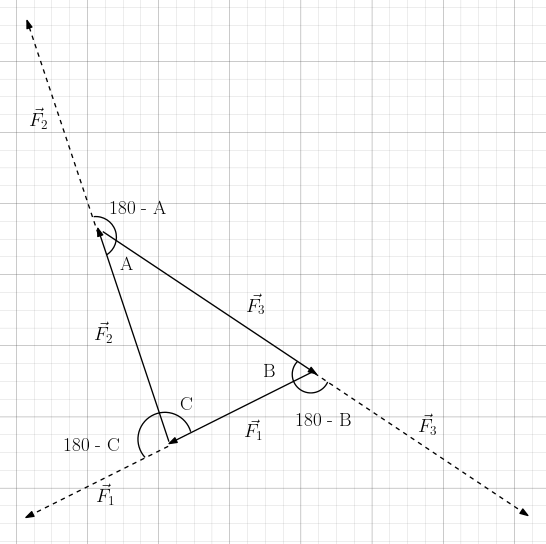
Bu şekli dikkatlice inceleyelim. İlk şekle göre iki değişiklik yaptık. İlki kuvvet vektörlerini taşıyarak bir üçgen oluşturmak. İkincisi de her vektörün aynısından kesikli çizgili bir tane daha kendi ucuna eklemek. Önce ikinci işi neden yaptık onu açıklayalım. Kesikli çizgili gösterilen kuvvet vektörlerinin başlangıç noktalarını birleştirirseniz ilk şeklin aynısını elde edeceksiniz.
- F1 ile F3 arasındaki açının bu durumda 180 – B olduğunu gördünüz mü, ilk şekilde bu açıya β demiştik. β = 180 -B
- F2 ile F3 arasındaki açının bu durumda 180 – A olduğunu gördünüz mü, ilk şekilde bu açıya α demiştik. α = 180 – A
- F1 ile F2 arasındaki açının bu durumda 180 – C olduğunu gördünüz mü, ilk şekilde bu açıya θ demiştik. θ = 180 – C
Bu bilgiler biraz sonra işimize yarayacak. İlk işi neden yaptık, sinüs teoremini kullanmak için. Sinüs teoremi ya da kuralını hatırlamıyorsanız hemen hatırlatalım: Bir üçgende kenarların karşılarındaki iç açıların sinüslerine oranları birbirine eşittir. Buna göre:
\frac{F_1}{sin A} = \frac{F_2}{sin B} = \frac{F_3}{sin C}
Bir trigonometri bilgisi daha: her hangi bir açının sinüsü, o açının bütünlerinin sinüsüne eşittir. Yani:
- sinA = sin(180-A) = sinα
- sinB = sin(180-B) = sinβ
- sinC = sin(180-C) = sinθ
Örnek soru 1
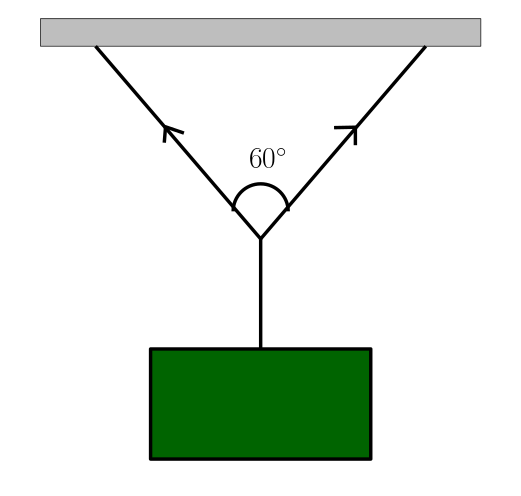
Kütlesi 3 kg olan bir cisim şekilde gösterildiği gibi tavandan esnemeyen iplerle asılmıştır. Cisim dengelendiğinde iplerdeki gerilimlerin büyüklüğü eşit olduğuna göre, bir ipteki gerilim kaç Newtondur? (g = 10 m/s2)
Çözüm
Bu soruyu çözmek için gereken tek şey açıları belirlemek. Resmi tekrar inceleyip açıları belirleyelim.
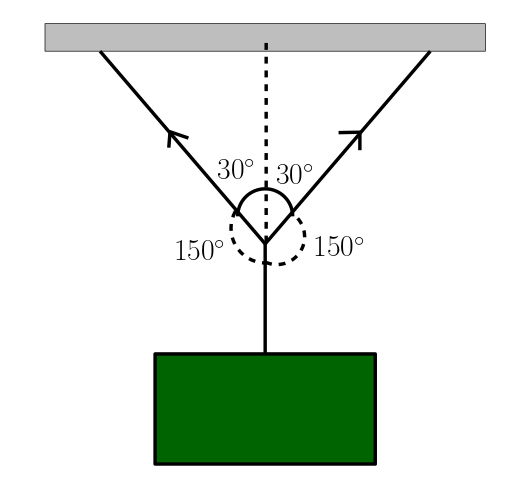
Cismin bağlı olduğu ip yere dik, uzantısı iki ipin tam ortasından geçiyor. Öyleyse açılarımızı bulduk. Şimdi Lami teoremini iplerden birine uygulayalım.
\frac{T}{sin150^\circ} = \frac{mg}{sin60^\circ}
Cismin ağırlığı kütlesiyle yerçekimi sabitinin çarpımına eşit. mg = 3 x 10 = 30 N
150 derecenin sinüsü de 30 derecenin sinüsüne eşit.
T = 30 \times \frac{sin 150^\circ}{sin 60^\circ} = 30 \times \frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}} = 30 \times \frac{\sqrt{3}}{3} = 10 \sqrt{3} N
Örnek soru 2
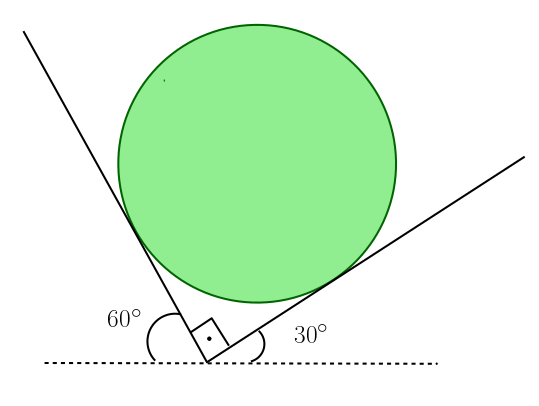
100 N ağırlığındaki küre şeklindeki cisim şekildeki gibi iki sabit duvarın arasında dengede durmaktadır. Buna göre duvarların küreye uyguladıkları tepki kuvvetleri kaç Newtondur?
Çözüm
Yine bütün mesele şekli geometrik olarak yorumlayabileceğimiz biçimde çizebilmekte.
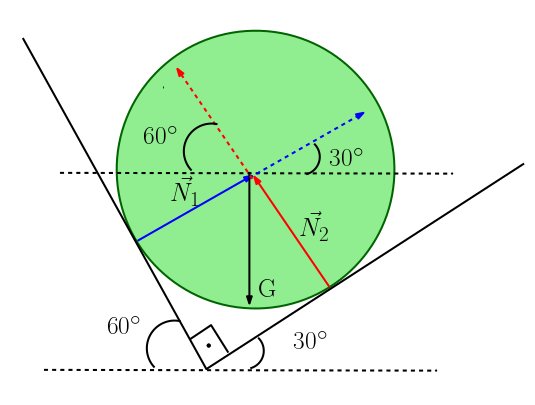
Mavi okla gösterilen birinci duvarın küreye dokunduğu noktada uyguladığı tepki kuvveti. Kırmızı okla gösterilen de ikinci duvarın küreye uyguladığı tepki kuvveti. Siyah ok cismin ağırlık vektörü. Mavi, kırmızı ve siyah vektörlerin başlangıç noktalarını kesiştirirsek bakın ortaya ne çıkıyor. Kesikli çizgi yerdi, ona paralel bir kesikli çigi daha çizdik ve açılarımızı belirledik.
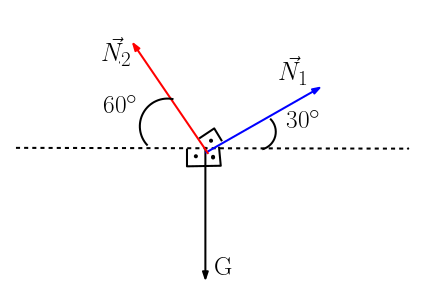
Serbest cisim diyagramı haline getirince daha net görebiliyoruz. Artık tek yapmamız gereken sırayla Lami teoremini uygulamak. Önce birinci tepki kuvvetini bulalım.
\frac{N_1}{sin150^\circ} = \frac{100}{sin 90^\circ}
Şimdi ikinci tepki kuvvetini bulalım.
\frac{N_2}{sin120^\circ} = \frac{100}{sin 90^\circ}
Bu sorular bize Bernard Lamy’ye teşekkür etmemiz gerektiğini hatırlatıyor. Çok karmaşık gibi görünen problemleri, hızlı çözebilmemizi sağladığı için.
Lami Teoremiyle ilgili Kazanımlar
11.1.9.1. Cisimlerin denge şartlarını açıklar.