Sabit Makara, Hareketli Makara ve Palanga nedir?

İnşaat gördüyseniz makara da görmüşsünüzdür. İnşaat işçileri malzemeleri üst katlara nasıl çıkarıyorlar? Makaralarla. Makaralar tekerlek biçiminde merkezinden geçen eksen etrafında serbestçe dönebilen sistemlerdir. Makaralara bir ip geçirilir ve ipe uygulanan kuvvetin yönü ya da büyüklüğü değiştirilebilir. Basit makine sistemlerindeki kullanım amaçlarına göre makaralar sabit makaralar ya da hareketli makaralar olmak üzere iki farklı şekilde kullanılabilir: sabit ve hareketli. Bu makara türlerini birleştirerek ürettiğimiz diğer basit makine sistemlerine de palangalar diyoruz.

Sabit Makara nedir?

Sabit makara adı üzerinde, öteleme hareketi yapmayan makaradır. Bu makara sadece sabit bir eksen üzerinde dönme hareketi yapar. Sabit makaranın kullanılma nedeni uygulanan kuvvetin yönünü değiştirmektir. Aşağıdaki şekilde inceleyelim.

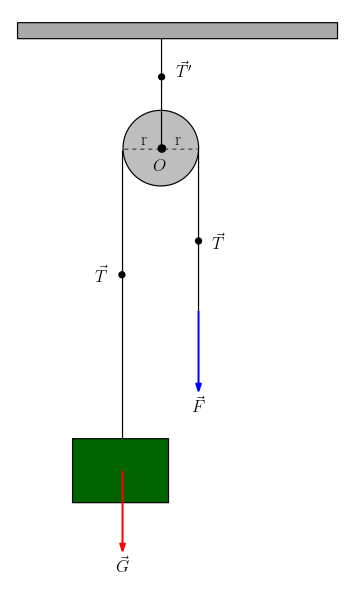
• Sürtünme ve ip ağırlıklarını ihmal ediyoruz. Ayrıca iplerin esnemediğini ve sıkışmadığını kabul ediyoruz.
• Sabit makara ya dönmüyor ya da sabit açısal hızla dönüyor. Bu nedenle O noktasına uygulanan net tork sıfır.

\vec{\tau}{toplam} = \vec{\tau}G + \vec{\tau}_F

O noktasına göre F ve G kuvvetlerinin torkları zıt yönlü öyleyse: (r makaranın yarıçapı)
Gr = Fr

G = F; \space \frac{G}{F}=1

Yani kuvvet kazancı yok. Dolayısıyla yoldan da kayıp yok. F tarafında ip x kadar aşağı çekilirse, G tarafında ip x kadar yukarı çıkıyor. Ama yükü kaldırmak için yukarı yönlü kuvvet uygulamaktan kurtulduk, aşağı çekerek (ağırlıkla aynı yönde) yükü kaldırabiliyoruz.

• İpin her noktasındaki gerilme kuvveti T eşittir. İp kuvveti aktarır. Gerilmenin büyüklüğü T = F = G olur.
• Sistem dengede ise makaranın tavana bağlı bulunduğu ip teki T’ kuvveti, net kuvvetin eşit olması gerektiği için şöyle bulunur:

\vec{F}_{net} = 0; \space 0 = \vec{T'} + \vec{G} + \vec{F} |\vec{T'}| = |\vec{G}| + |\vec{F}| = 2F

Yani T’ gerilmesinin büyüklüğü G+F’e eşit olur.

Makaranın ağırlığı sıfırdan farklı olursa:
|\vec{T'}| = |\vec{G}| + |\vec{F}| + |\vec{G}_{makara}|

Makaranın ağırlığının olması uygulanan kuvveti etkilemez; yalnızca makarayı taşıyan ipteki gerilme kuvvetini artırır.

Örnek soru 1

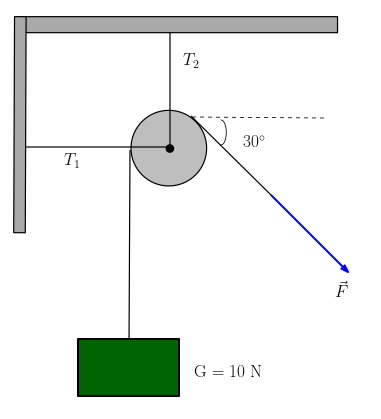
Şekilde gösterilen sürtünmelerin ihmal edildiği ve esnemeyen iplerle kurulan sistemde makaranın ağırlığı 4 N, yükün ağırlığı 10 N’dur. Sistem F kuvveti ile dengelendiğine göre iplerdeki gerilimlerin oranı (T₁ / T₂ )kaçtır?

Çözüm

• Sürtünmeler ihmal edildiğine ve ip esnemediğine göre aynı ip üzerindeki tüm noktaların gerilimi aynıdır. Yani G = F = 10 N.
• Sistem dengede olduğuna göre makaraya etkiyen kuvvetlerin toplamı sıfırdır. Önce makaranın serbest cisim diyagramını çizelim.

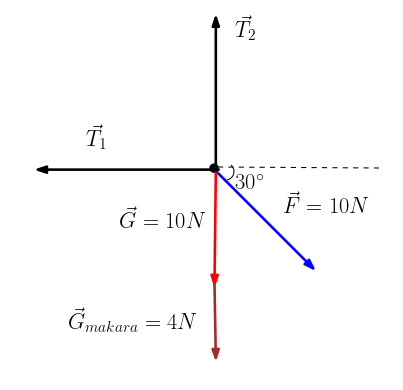
Şimdi kuvvetleri x ve y bileşenlerine ayırıp inceleyelim. x bileşeninde sola doğru T₁, sağa doğru Fcos30° var sadece. Öyleyse:
T_1 = 10(\frac{\sqrt{3}}{2}) = 5\sqrt{3} \space N

y bileşenlerinde +y yönünde (yukarı doğru) T₂, -y yönünde (aşağı doğru) G, G_makara ve Fsin30° var. Öyleyse:
T_2 = G + G_{makara} + Fsin30^\circ = 10 + 4 + 10(\frac{1}{2}) = 14 + 5 = 19 \space N

Artık istenen oranı bulabiliriz.
\frac{T_1}{T_2} = \frac{5\sqrt{3}}{19}

Hareketli makara nedir?

Hareketli makara etrafına sarılmış bir ip aracılıiğıyla dönerek yükle birlikte öteleme hareketi yapan sisteme denir. Hareketli denmesinin nedeni de budur, yani yükle birlikte hareket etmesi. Aşağıdaki şekilde F kuvveti (yükü dengeleyen bir kuvvet bu F = T = G/2 yani) yukarı doğru ipi çekiyor, ipin diğer ucu tavana bağlı, dolayısıyla makara ve yük sabit hızla yukarı doğru hareket ediyor.

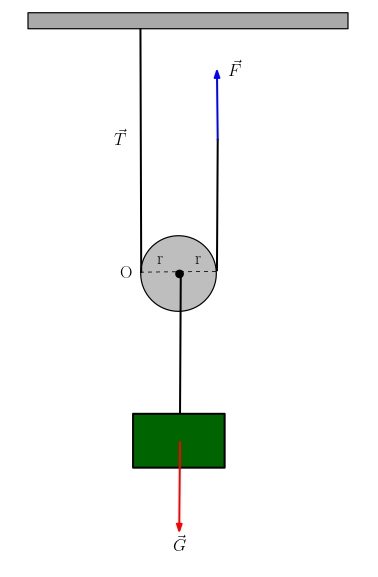
Şimdi de torku inceleyelim. Makaranın tavana bağlı olan ipin bulunduğu ucundaki O noktasına göre net torkun sıfır olması lazım. Çünkü sistem dengede.
\vec{\tau}_{net} = \vec{G} \times r + \vec{F} \times 2r = 0

İpin gerilme kuvveti (T) torku hesapladığımız noktadan geçtiği için torka katkısı sıfır. Ayrıca T = F olduğuna da dikkat edin. Yine buraya kadar makaranın ağırlıksız olduğunu varsaydığımızı da hatırlatalım.
Gr = 2Fr

F = \frac{G}{2}; \space \frac{G}{F} = 2

F kuvveti yükün ağırlığının yarısına eşit. Kuvvet kazancımız iki, yani uyguladığımız kuvvetin iki katı miktarda yük kaldırabiliyoruz. Ama yoldan da iki
kat kaybediyoruz. Peki yoldan kazancımız ya da kaybımız var mı? İş ve enerji ilişkisine bakalım. Yük h kadar yükseldiğinde F ipi x kadar çekmiş olsun.
W = Fx = Gh

G = 2F Fx = 2Fh x = 2h ; \space h = \frac{x}{2}

Yani x kadar çekersek yük x/2 kadar yükseliyor. Yoldan iki kat kaybediyoruz. Enerjinin korunduğu bir evrende başka türlüsü de düşünülemezdi.

Örnek soru 2

Ağırlığı 30 N olan hareketli makara ile ağırlığı G olan bir cisim şekildeki gibi F kuvvetiyle dengeleniyor. İp en fazla 80 N gerilme kuvvetine dayanabildiğine göre bu sistemle taşınabilecek en fazla yük kaç Newton olur?

Çözüm

Sistem dengedeyse makaraya etki eden net kuvvet sıfırdır. Öyleyse:
\vec{F}{net} = 0 = \vec{T} + \vec{F} + \vec{G} + \vec{G}{makara}

T = F = 80 \space N 80 \space N + 80 \space N = G + 30 \space N G = 160 \space N - 30 \space N = 130 \space N

Palanga nedir?

Palangalar birden çok makaranın farklı şekillerde bağlanmasıyla elde edilen sistemlerdir. Palangalarda sabit ve hareketli makaralar bir arada kullanılır. Sadece kuvvetten daha çok kazanmak için değil aynı zamanda uygulanacak kuvvetin yönünün belirlenmesi için de kullanılırlar. Aşağıdaki şekilde bir palanga gösteriliyor.

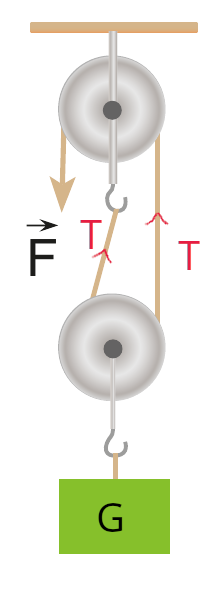
Makaralar ve ip ağırlıksız sa G kaç F olur? Önce iplerdeki gerilme kuvvetlerini göstermeliyiz. Alttaki hareketli makaranın iki yanındaki iplerin gerilme kuvvetlerinin büyüklüğü birbirine eşit, T diyelim bu kuvvetlere. Üstteki sabit makaranın sağındaki T gerilme kuvveti de solundaki F kuvvetine eşit. Öyleyse T = F. Bu durumda G = T + T = 2T = 2F olduğunu gördünüz mü? Peki yoldan 2 kat kaybettiğimizi çıkarabilir misiniz? Yorumlarda cevaplarınızı bekliyorum.

Bir de bu sisteme çok benzeyen bir başka sisteme bakalım.

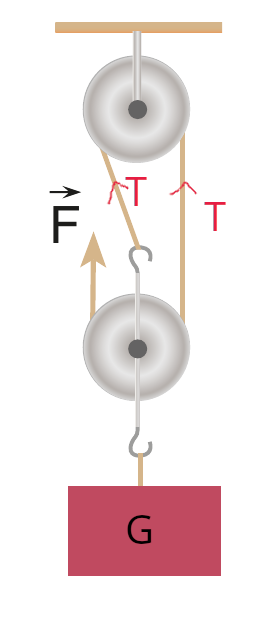
Bu kez G kaç F olur? Aşağıdaki hareketli makaranın solundaki F ile sağındaki T gerilme kuvveti eşit, görebildiniz mi? Yukarıdaki sabit makaranın solundan ve sağından geçen iplerdeki gerilme kuvvetleri de eşit. Bu yükü yukarı doğru F+T+T = 3F kuvvet çekiyor. Demek ki G = 3F. Peki yoldan üç kat kaybettiğimizi gördünüz mü? Yorumlarda cevaplarınızı bekliyorum.

Makaralar ve Palangalarla ilgili Kazanımlar

11.1.10.1. Günlük hayatta kullanılan basit makinelerin işlevlerini açıklar.

• Kaldıraç, sabit ve hareketli makara, palanga, eğik düzlem, vida, çıkrık, çark ve kasnak ile sınırlı kalınır.

11.1.10.2. Basit makineler ile ilgili hesaplamalar yapar.

• İkiden fazla basit makinenin bir arada olduğu sistemlerle ilgili matematiksel hesaplamalara girilmez.
• Hesaplamaların günlük hayatta kullanılan basit makine örnekleri (anahtar gibi) üzerinden yapılması sağlanır.
• Basit makinelerde verim ile ilgili matematiksel hesaplamalar yapılması sağlanır.