Sınır açısı ve tam yansıma nedir?

Snell Yasası bize ışığın kırılma indisi küçük olan ortamdan kırılma indisi büyük olan ortama geçişinde her zaman kırılma açısının gelme açısından küçük olduğunu söylüyor.

Bu bilgiye dayanarak şu soruyu soralım: Işık, kırılma indisi küçük olan ortamdan kırılma indisi büyük olan ortama daima geçebilir mi? Cevabını Bükülen Işık PHET Simülasyonundan elde ettiğim aşağıdaki resimle vermeyi deneyelim.

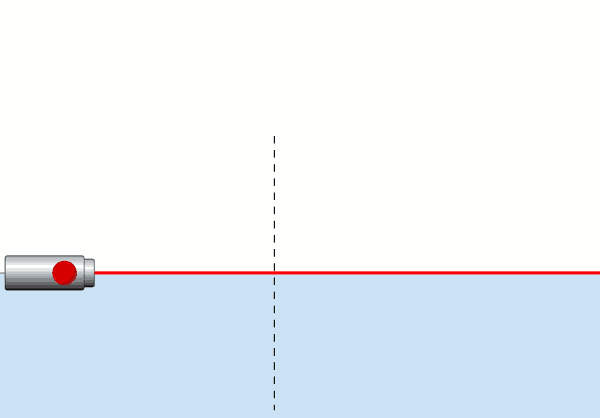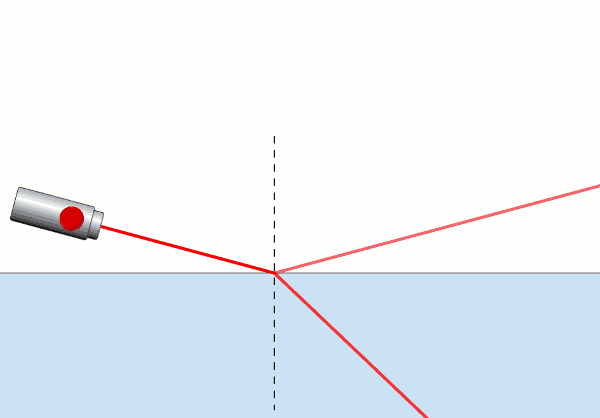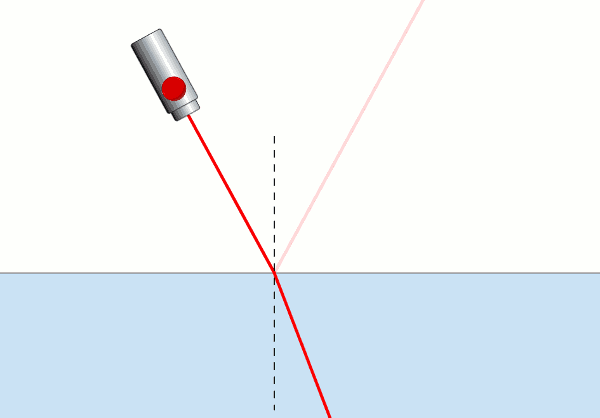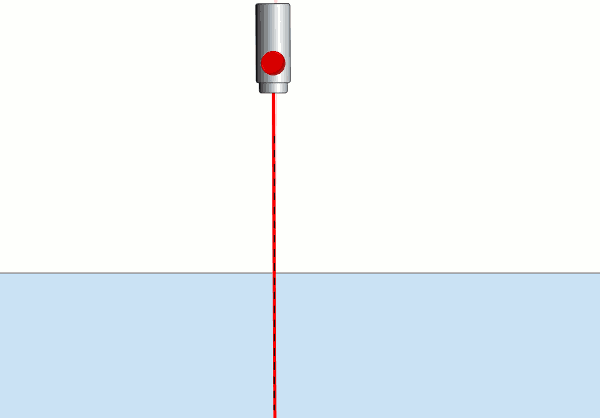
Resmin üst kısmı (beyaz bölge) hava, alt kısmı (mavi bölge) su. Lazer ışığını normalle 90°’den başlayıp 0°’ye kadar gelme açısı yapacak şekilde döndürüyoruz. Sadece 90°’de ışık su yüzeyine paralel gidiyor, bunun dışındaki tüm durumlarda (gelme açılarında) havadan (optik olarak az yoğun ya da kırılma indisi düşük ortamdan) suya (optik olarak çok yoğun ya da kırılma indisi yüksek ortama) geçiyor.

Şİmdi bu soruyu tersten soralım. Yine Snell yasasına göre ışığın kırılma indisi büyük olan ortamdan kırılma indisi küçük olan ortama geçişinde her zaman kırılma açısının gelme açısından büyük olduğunu biliyoruz. Öyleyse, ışık, kırılma indisi büyük olan ortamdan kırılma indisi küçük olan ortama her zaman geçebilir mi? Bu soruyu da yine simülasyonu kullanarak inceleyelim.

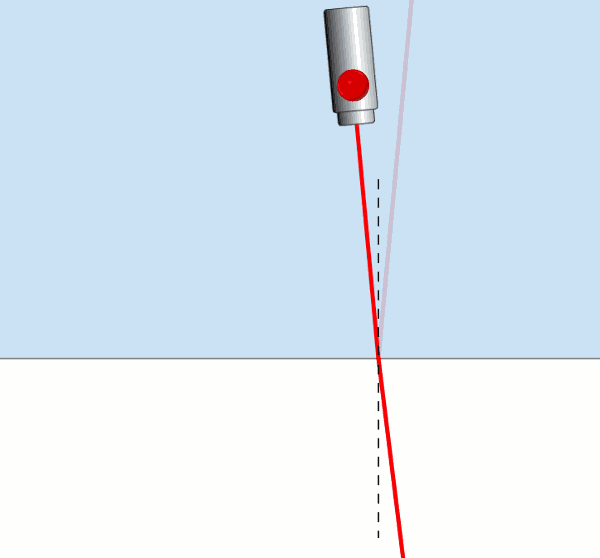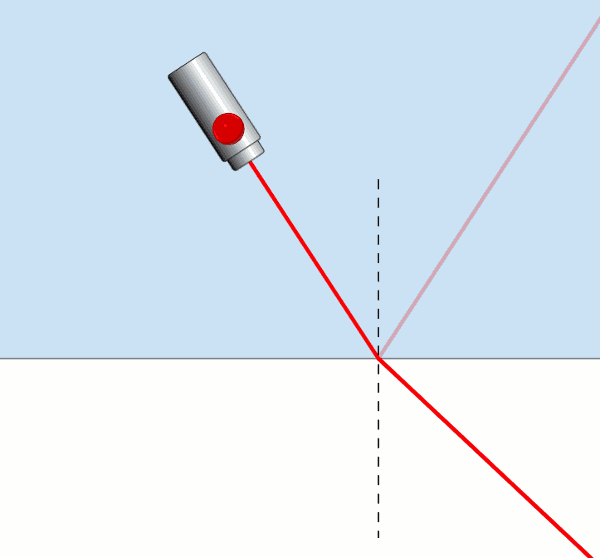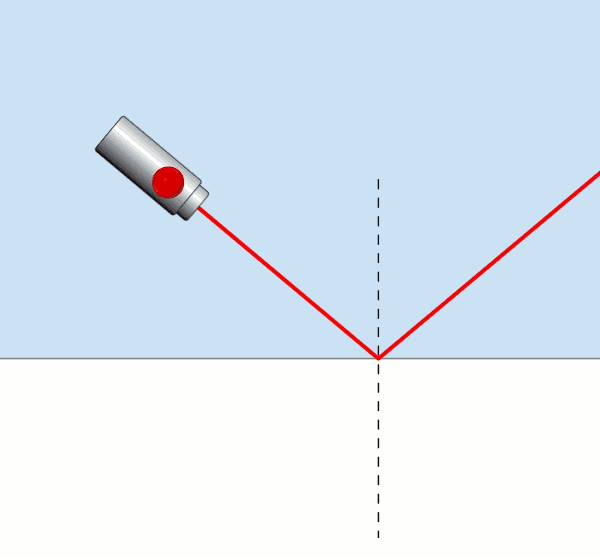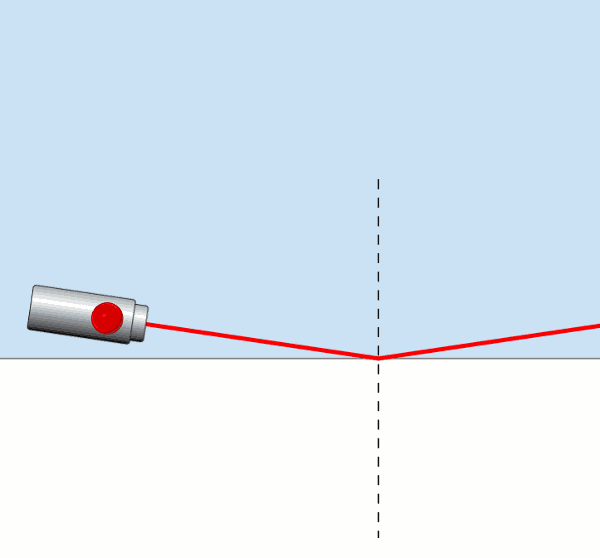
Resme dikkatli bakarsanız ışık sudan havaya belli bir açıya kadar geçebiliyor. Ama belli bir gelme açısına ulaştığında ışık su – hava yüzeyine paralel olarak kırılyor, bu yüzeyi yalıyor, kırılma açısı 90° oluyor. İşte bu açıya sınır açısı deniyor. Gelme açısı sınır açısından büyük olduğu zaman ise kırılma olayı gerçekleşmiyor, ışık az yoğun ortama geçemiyor, ışık su – hava yüzeyinden tamamen yansıyor , bu olaya da tam yansıma adı veriliyor.

Sınır açısı nasıl hesaplanır?

Sınır açısının ne olduğunu öğrendik, ama nasıl buluruz? Örneğin, su ile hava arasındaki sınır açısını nasıl hesaplarız? Snell Kanunu bunun için çok işimize yarayabilir:

n_susin(θ) = n_havasin(90°)

Kırılma açısının 90° olduğuna (yani hava – su yüzeyine paralel giden ışının normalle 90° açı yaptığına) dikkat edin.

n_su = 1,33, n_hava = 1 ve sin(90°) = 1

Öyleyse:

sin(θ) = 1/1,33

Sinüsü 1/1,33 olan açıyı arcsin (sinüsün ters fonksiyonu) fonksiyonuyla bulabiliriz.

θ = arcsin(1/1,33) = 48°

Yani suyun sınır açısı 48°’dir.

Sınır açısı ve tam yansıma ile ilgili günlük hayattan örnekler

Serap olayı tam yansıma nedeniyle gerçekleşir. Yazın bir yolda giderken uzağa baktığınızda asfaltın üstünü ıslakmış gibi gördüğümüz olmuştur. Isınan havanın hacmi genişler, özkütlesi azalır, kaldırma kuvvetinden dolayı yükselir. Yerden yüksekteki sıcak havanın kırıcılık indisi de azalır. Alçaktaki hava tabakası ile yüksekteki hava tabakası arasındaki kırıcılık indisi farkı ışığın kırılmasına ve buna bağlı olarak serap olayına neden olur.

Fiberoptik kablolar da tam yansıma olayı kullanılarak tasarlanır. Cam liflerin içine gönderilen ışık cam lifin çeperinden yansır bu nedenle cam lifin içine hapsolur. Böylece ışık kullanılarak uzak mesafeler arasında sinyal göndermek mümkün hale gelir.

Sınır açısı ve tam yansıma ile ilgili kazanımlar

2017 – 10.4.6.2. Işığın tam yansıma olayını ve sınır açısını analiz eder.

• Tam yansıma ve sınır açısı ile ilgili matematiksel hesaplamalara girilmez.
• Tam yansıma ve sınır açısı ile ilgili hesaplamalar yapılması sağlanır. (Fen lisesi)
• Tam yansımanın gerçekleştiği fiber optik teknolojisi, serap olayı, havuz ışıklandırması örneklerine yer verilir.
• Öğrencilerin deney veya simülasyonlarla oluşturulan tam yansıma olayını ve sınır açısını yorumlamaları sağlanır.