Suyla oynayan herkes bilir. Suya taş atarsanız batar, tahta atarsanız yüzer. Ama neden taş batıyor, tahta yüzüyor? Su tahtayı kaldırıyor (yukarı doğru itiyor), peki taşı kaldırmıyor mu? Bu yazıda kaldırma kuvveti kavramını durgun akışkanların (sıvıların ve gazların) içlerine konulan cisimlere uyguladığı kuvvet olarak tanımlayacak, kaldırma kuvvetinin sebebini (nedenini) araştıracak ve hangi değişkenlere bağlı olduğunu bulacağız. Sonra da Arşimet prensibi (Archimedes ilkesi veya yasası) neymiş, açıklayacağız. Genel olarak sıvıların kaldırma kuvvetinden bahsediyor olacağız, sonra gazların kaldırma kuvvetini inceleyeceğiz. Önce akışkanların kaldırma olayını görelim ve temel kavramlara göz gezdirelim.
Görünür ağırlık nedir?
Hiç denizin içindeki bir taşı kaldırmaya çalıştınız mı? Taşın, suyun içindeyken suyun dışında olduğundan daha hafif olduğunu fark etmiş olmalısınız. Hafif ne demek? Ağırlığı daha az demek, nasıl oluyor da suyun içinde bir cismin ağırlığı azalabiliyor? Ağırlığın kütleden farklı olduğunu hatırlayalım, ağırlık yer çekiminden kaynaklanan bir kuvvetti, kütle ise madde miktarı. G = mg. Peki suyun içinde bir cismi tartarsak ne buluruz? Aşağıdaki resimde kaldırma kuvveti PHET simülasyonunda tam olarak bunu yapıyoruz.
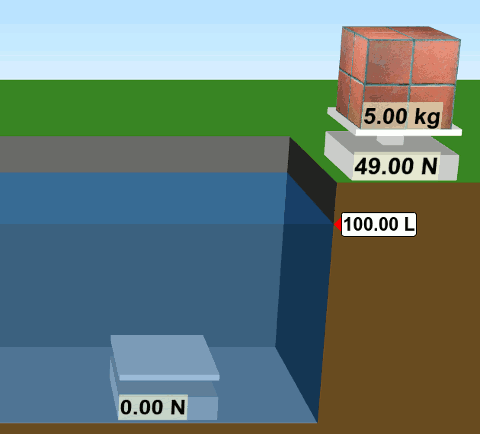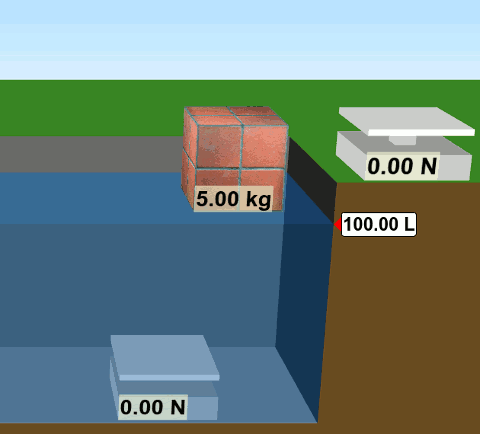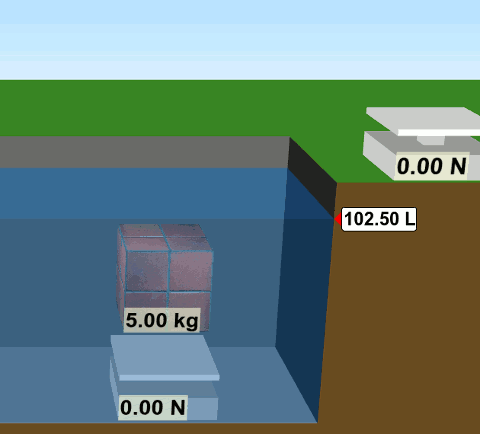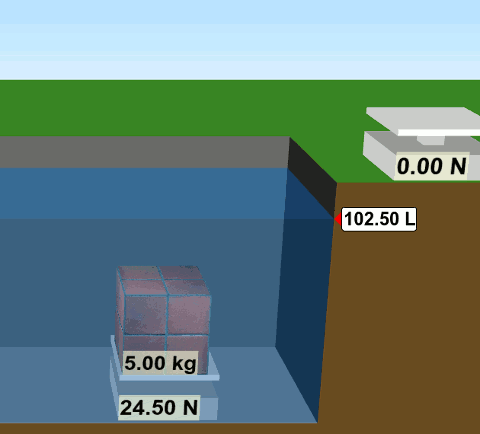
Küp şeklinde kütlesi 5 kg olan bir tuğlayı suyun dışında tarttığımızda ağırlığının 49 N olduğunu görüyoruz. (Yer çekimi ivmesi g= 9,8 m/s2 olarak alınmış.) Tuğlayı suyun içine taşıyıp tarttığımızda ise görünür ağırlığının 24,5 N olduğunu görüyoruz. İşte suyun içinde tarttığımız ağırlık değerine görünür ağırlık deniyor. Bu arada tuğla suyun içine girince suyun yükseldiğine (hacminin arttığına) dikkat edin. Arşimet ilkesinde kullanacağız bu bilgiyi.
Bir de bir tahtayı aynı şekilde tartalım bakalım ne olacak?
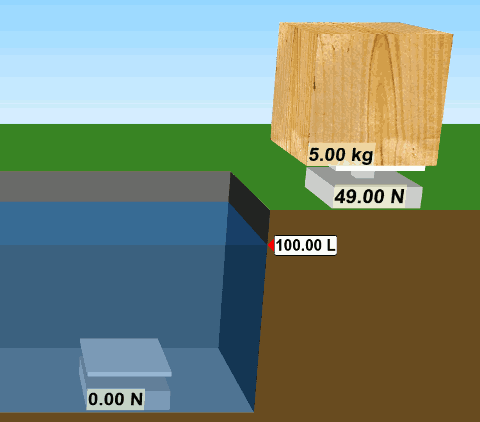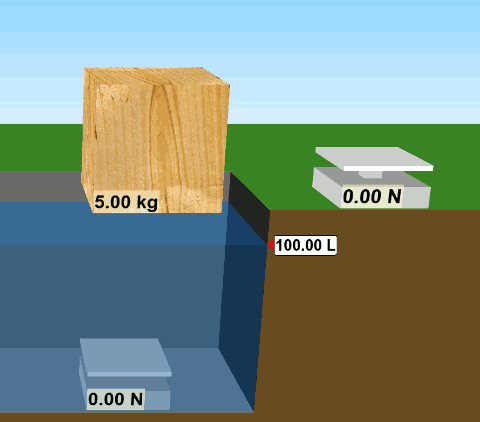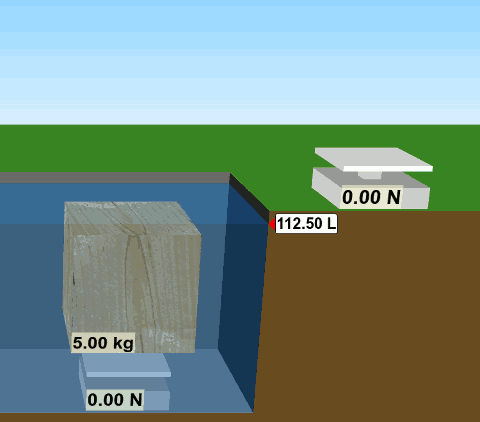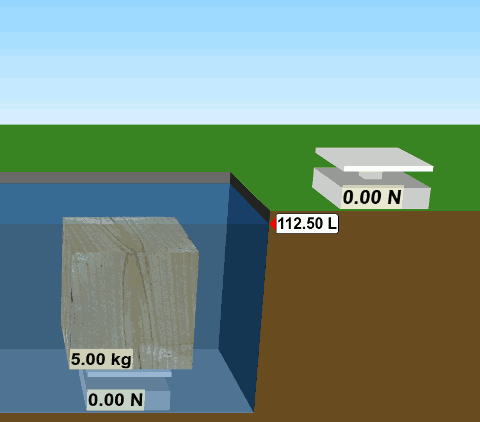
Tahta suyun dışındayken ağırlığı 49 N, kütlesi 5 kg. (G = mg, G = 5 kg x 9,8 m/s2 = 49 N). Suyun içine girdiği zaman batmıyor, yüzüyor. Benim fareyle tutup havuzun dibine kadar sürüklemem gerekiyor. Orada tarttığım zaman ise ağırlığının 0 N olduğunu, yani ağırlıksız olduğunu buluyorum. Tahtanın suyun içindeki görünür ağırlığı sıfır oluyor.
Hem tuğla hem tahta için suyun içindeki görünür ağırlığın suyun dışındaki gerçek ağırlıktan az olmasının nedeni, suyun bu cisimleri ağırlıklarının zıt yönüne (yani yukarı doğru) itmesi olmalı. İşte suyun (sıvıların hatta daha genel olarak akışkanların) içlerine konulan cisimleri yukarı doğru itmesine kaldırma kuvveti diyoruz.
Şimdi neler olduğunu anlamak için tuğlanın ve tahtanın suyun içindeki serbest cisim diyagramlarını çizelim.
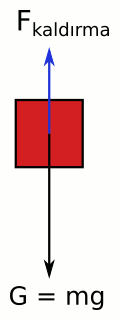
Tuğlanın serbest cisim diyagramında gerçek ağırlığının aşağı yönde ( G = mg) ve kaldırma kuvvetinin yukarı yönde olduğunu görüyoruz. Kaldırma kuvvetinin gerçek ağırlıktan daha az olduğunu da görüyoruz (mavi ok siyah oktan daha kısa). Bu iki kuvvet vektörünün farkı aşağı yönlü görünür ağırlığa eşit:
Ggörünür = mg – Fkaldırma
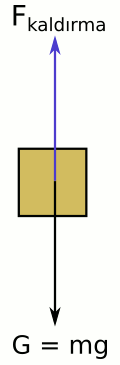
Tahtanın serbest cisim diyagramında yine gerçek ağırlığının aşağı, kaldırma kuvvetinin yukarı yönlü olduğunu görüyoruz. Bu kez bu iki kuvvet birbirine eşit (siyah ve mavi okların uzunlukları aynı). Birbirinden çıkardığımız zaman sonucun sıfır olduğunu görüyoruz. Tahta suyun içinde ağırlıksız.
Ggörünür = mg – Fkaldırma
Ggörünür = 0
mg = Fkaldırma
Kaldırma kuvvetinin sebebi nedir?
Kuvvet durup dururken uygulanmaz, bir nedeni olmalı. Sıvının içine koyduğumuz bir cisme neden kaldırma kuvveti uygulanıyor olabilir? Basınç ile ilişkili olmalı. Aşağıdaki resimde bir sıvının içine tamamen batmış, askıda bir cismi inceliyoruz.
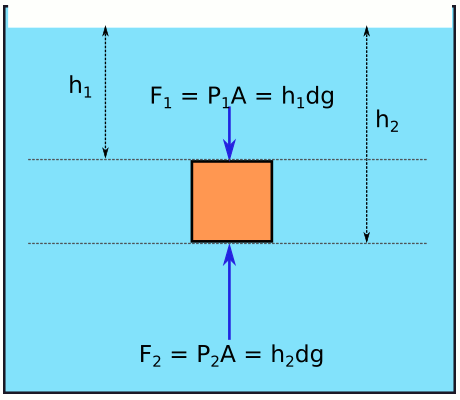
Cisim sıvının içinde olduğuna göre, sıvı cisme her noktada basınç uygular. Biz basınç kuvvetiyle ilgileneceğiz. Basınç kuvvetinin F = PA olduğunu öğrenmiştik. Sıvı basıncının da P = hdsıvıg olduğunu biliyoruz. Öyleyse cismin üst yüzeyindeki ve alt yüzeyindeki (tabanındaki) basınç kuvvetlerini hesaplayabiliriz.
Füst = P1A
P1 = h1dsıvıg
Füst = h1dsıvıgA
h1 cismin üst yüzeyindeki sıvının derinliğini,
d sıvının özkütlesini,
g yer çekimi ivmesini,
A ise cismin üst kısmının yüzey alanını simgeliyor.
Şimdi de cismin alt yüzeyi için basınç kuvvetini bulalım.
Falt = P2A
P2 = h2dsıvıg
Falt = h2dsıvıgA
h2 cismin alt yüzeyindeki sıvının derinliğini gösteriyor.
Cismin alt ve üst yüzeyine sıvı tarafından uygulanan basınç kuvvetleri eşit mi, yoksa aralarında bir fark var mı? h2‘nin açıkça h1‘den daha büyük olduğunu görüyoruz. Öyleyse cismin alt yüzeyine uygulanan basınç kuvveti üst yüzeyine uygulanandan daha büyük olmak zorunda.
Öyleyse kaldırma kuvvetinin sebebinin cismin alt ve üst yüzeyleri arasındaki sıvının basınç farkından kaynaklanan basınç kuvveti farkı olduğu sonucuna varabiliriz.
Şimdi de kaldırma kuvvetinin formülü neymiş onu bulalım: (cismin tabanının ve tavanının yüzey alanlarının eşit olduğuna dikkat edin.)
Fkaldırma = P2A – P1A
Fkaldırma = (h2-h1) dsıvıgA
Bu bir küp, hacminin (V ile gösteriyoruz) taban alanı çarpı yükseklik olduğunu biliyoruz. Yüksekliğin de (h2-h1) olduğunu görüyoruz. Tabanın ve tavanın yüzey alanları birbirine eşit, çünkü bu bir küp (dikdörtgenler prizması olsa da aynı olurdu). Öyleyse,
V = (h2-h1)A
Hacmi yerine koyarsak: Fkaldırma = Vdsıvıg
Peki ya yan yüzeyler ne olacak?
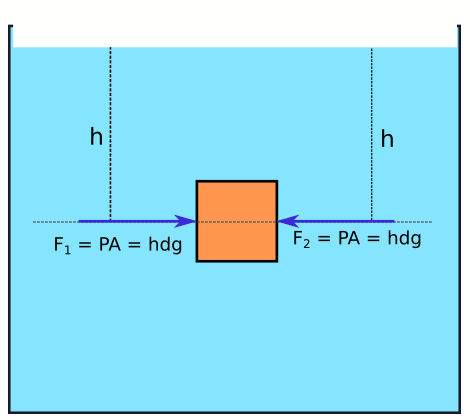
Aşağıdaki resimde gösterildiği gibi, yan yüzeylerin derinliği aynı olduğu için sıvı basıncı da aynıdır, bu nedenle uygulanan basınç kuvvetleri eşittir.
İşte bu yüzden kaldırma kuvvetinin yönü hep yukarı (ağırlığın yani yer çekimi kuvvetinin zıt yönüne) doğrudur.
Arşimet prensibi nedir?
Arşimet prensibi (Archimedes ilkesi veya yasası) en genel haliyle “tamamen ya da bir kısmı bir akışkana batan cisme akışkan tarafından uygulanan kaldırma kuvvetinin cismin yer değiştirdiği akışkanın ağırlığına eşit” olduğunu söyler. Akışkan yerine sıvı dersek, bir sıvının içine konulan bir cisme uygulanan kaldırma kuvveti cismin taşırdığı sıvının ağırlığına eşittir.
Bu cümleyi matematiksel olarak anlamaya çalışalım.
Kaldırma kuvveti = Taşan sıvının ağırlığı
Taşan sıvı ne demek ve taşan sıvının ağırlığını nasıl buluruz? Ağzına kadar su dolu bir bardağın içine bir kaç tane buz küpü atarsanız ne olur? Su bardaktan dışarı taşar. Eğer bardaktan taşan suyu bir kabın içinde biriktirip tartarsanız, taşan suyun ağırlığını bulmuş olursunuz. Ayrıca hacim nasıl ölçülür sorusunda taşırma kabı kullanarak cisimlerin hacimlerinin ölçülebileceğini de öğrenmiştik.
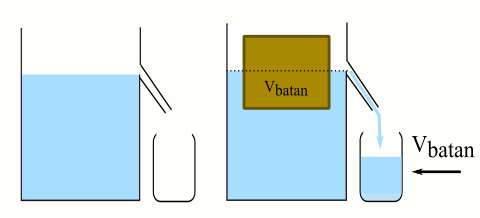
Aşağıdaki resimde taşırma kabına konan düzgün bir cisim görülüyor. Cismin batan kısmının hacminin taşırdığı sıvının hacmine eşit olduğunu görüyoruz. Çünkü suyun yerini cismin sıvıya batan hacmi alıyor. Taşan suyun ağırlığının da kaldırma kuvvetine eşit olduğunu söylüyor Arşimet prensibi.
Ayrıca yukarıdaki görünür ağırlık bölümündeki havuza atılan tuğla ve tahta blok resimlerine dikkatli bakarsanız, suyun hacminin ne kadar değiştiğini görebilirsiniz. İki durumda da tuğla bloğun da tahta bloğunda batan hacimleri taşırdıkları suyun hacmine eşit.
Öyleyse kaldırma kuvvetinin formülünü bir de şöyle yazabiliriz:
Fkaldırma = msıvıg
Taşan sıvının kütlesini hacim ve özkütle cinsinden ifade edersek:
m = dsıvıVbatan
Kaldırma kuvveti de:
Fkaldırma = dsıvıVbatang
Bir önceki bölümde, basınç kuvveti farkının kaldırma kuvvetinin sebebi olduğunu bulduğumuzda da kaldırma kuvvetini şöyle yazmıştık:
Fkaldırma = Vdsıvıg
Bu formülde V aslında cismin suyun içinde kalan yani batan hacmini gösteriyor. V yerine Vbatan yazmamız daha uygun olur.
Fkaldırma = Vbatandsıvıg
Gördüğümüz gibi kaldırma kuvveti her iki yoldan da aynı çıkıyor, demek ki akıl yürütmemiz tutarlı.
Son bir soru, Arşimet ilkesini kullanarak cisimlerin özkütlelerini bulabiliriz, ama nasıl?
Kaldırma kuvveti nelere bağlıdır?
Kaldırma kuvvetinin matematiksel modeli yani formülü özünde kaldırma kuvvetinin bağlı olduğu değişkenleri özetliyor:
Fkaldırma = Vbatandsıvıg
- Cismin sıvının içine batan hacmi artarsa kaldırma kuvveti artar. Plastik bir topu suyun içine bastırırsanız, daha çok batırdıkça suyun topu yukarıya doğru daha çok ittiğini görürsünüz.
- Sıvının özkütlesi arttıkça kaldırma kuvveti artar. Denizde yüzmek havuzda yüzmekten kolaydır, çünkü tuzlu suyun özkütlesi, saf suyun özkütlesinden (havuzdaki su tam olarak saf su olmasa da) daha fazladır.
- Yer çekimi ivmesi artarsa kaldırma kuvveti de artar.
Yüzme, askıda kalma, batma nedir?
Yüzme, bir sıvıya bırakılan cismin hacminin bir kısmının sıvının içinde, bir kısmının sıvının dışında olmasıdır. Yani yüzen bir cisim sıvıya kısmen batmıştır. Aşağıdaki resimde A cismi strafordan B cismi buzdan yapılmış ve suyun içine bırakılmış, ikisi de yüzüyor.

Yüzen cisimlerde kaldırma kuvveti cismin ağırlığına eşittir. Yani cisim dengelenmiş kuvvetlerin etkisi altındadır. Yukarıdaki resimde strafordan yapılmış olan cisme mi, yoksa buzdan yapılmış olan cisme mi etkiyen kaldırma kuvveti daha fazla? Neden? Ayrıca bir cisim yüzüyorsa cismin özkütlesi sıvınınkinden mutlaka küçüktür. Neden? (Yorumlara cevaplarınızı yazabilirsiniz.)
Askıda kalma, cismin tamamının sıvının içinde olmasına rağmen sıvının tabanına inmemiş olması durumudur. Cismin hacminin tamamının sıvının içinde olduğuna dikkat etmelisiniz. Askıda kalma durumunda da cismin ağırlığı kaldırma kuvvetine eşittir. Askıda kalan bir cismin yoğunluğu (özkütlesi) sıvının yoğunluğuna eşit olmak zorundadır. (Neden?)
Aşağıdaki resimde iki cisim farklı derinliklerde suyun içinde askıda kalmış. Derinliklerin farklı olmasının nedeni, birinin onları o derinlikte bırakmış olması.

Batma, cismin sıvının bulunduğu kabın tabanına inmiş olması ve cismin tamamının sıvının içinde bulunmasıdır. Batan bir cisme uygulanan kaldırma kuvveti her zaman cismin ağırlığından küçüktür. (Neden?) Bir cisim batıyorsa cismin özkütlesi mutlaka sıvının özkütlesinden büyüktür. (Neden?)
Aşağıdaki tuğla suyun içinde batıyor, çünkü suyun tabanındaki kantar (tartı) sıfırdan daha büyük bir kuvvet ölçüyor.

Gazların kaldırma kuvveti
Kaldırma kuvveti yalnızca sıvılar için değil tüm durgun akışkanlar için geçerlidir, dolayısıyla gazlar da içlerine konulan cisimlere kaldırma kuvveti uygular. En güzel örneği, uçan helyum balonları ya da sıcak hava balonlarıdır. Aşağıdaki resimdeki sıcak hava balonunun uçmasının nedeni atmosferin (havanın) balona uyguladığı kaldırma kuvvetidir.

Fkaldırma = Vbatandhavag
Balonun tamamı havanın içinde olduğu için:
Vbatan = Vbalon
Fkaldırma = Vbalondhavag
Eğer balonun özkütlesi havanın özkütlesinden küçükse kaldırma kuvveti balonun ağırlığından daha fazla olur. (Neden?)
Kaldırma kuvveti ile ilgili kazanımlar
2017 – 10.2.2.1. Durgun akışkanlarda cisimlere etki eden kaldırma kuvvetinin basınç kuvveti farkından kaynaklandığını açıklar.
- Archimedes ilkesi açıklanır. Yüzme, askıda kalma ve batma durumlarında kaldırma kuvveti ile cismin ağırlığının büyüklükleri karşılaştırılır.
- Kaldırma kuvveti ile ilgili matematiksel hesaplamalara girilmez.
- Kaldırma kuvveti ile ilgili hesaplamalar yapılır. (Fen lisesi)
Daha önce nasıl keşfedemedim çok güzel
Sorduğunuz soruların yanıtlarını yazının altına eklemeniz daha iyi olur bence.
O kısmını size bırakıyoruz. Soruları çözün cevaplarınızı yorumlarda gönderin tartışalım diye.
Biz zaten kaldırma kuvvetini F=Vb x dhava x g diye tanımlıyoruz ağırlığı ise m x g şeklinde. Biz burada m yerine dbalon x vbalon yazarsak sonuç olarak ağırlığı dbalon x vbalon x g şeklinde yazabiliriz. Burada F için yazdığımız Vb=V olduğundan ve yer çekimi de aynı olacağından dolayı farklılığı sağlayan özkütleleri oluyor. Başlangıçta da dhava>dbalon kabul edersek sonuç şuna varır: F>G. Bilmem yanlış mı yorumladım?
Öncelikle bu güzel anlatım için teşekkürü bir borç biliyor ve sorunuza kendi çapımda bir cevap vermek istiyorum
Yüzen cisimlerde kaldırma kuvveti cismin ağırlığına eşit ise;
vb.ds.g=vc.dc.g eşitliği sağlanmak zorundadır. Vb vc’den küçük olacağı için bu eşitliğin sağlanması gereğinden dcisim dsıvıdan küçük olmak zorundadır.
Çünkü balon askıda değildir.Bunu havuzun altında havuzun yoğunluğundan daha küçük bir cismi bırakmış gibi düşünebiliriz.
Balona uygulanan kaldırma kuvveti : V(balon) d(hava).g
Balonun ağırlığı: V(balon).d(balon).g
olduğu için balon net kuvvetin etkisiyle yukarı çıkar.
kaldırma kuvvetini küp ile açıklamışsınız, düzgün olmayan bir cisim ile basınç farklılığı yoluyla bulsak aynı sonuca ulaşır mıydık:/
Evet düzgün olmayan bir cisim için de basınç farkını kullanarak kaldırma kuvvetine ulaşırız.
kaldırma kuvvetinin sebebini anladım ama ya cismin alt tabanı ile üst tabanı birbirine eşit olmazsa? (ve diyelim cismin özkütlesi sıvının özkütlesine esit olsun)
Eğer cisim kapalı bir 3 boyutlu şekilse bütün yüzey normallerinin vectörlerini toplarsan yine kaldırma kuvvetini yönü ve büyüklüğüyle bulmuş olursun.
Fazlasıyla muhteşem sayın admin
Problem sorsam…
27 metre derinlikteki bir su kanalından kaç tonluk uçak gemisi geçemez?
Geçebilmesi için geminin eni, yüksekliği ve toplam ağırlığı ne kadar olmalı?
Kafamda ilgin kafamda ilginç bazı fikirler var belki bilinen şeyler bilmiyorum kafamda bazı düşünceler var doğrusudur kuralı varmıdır bilmiyorum. Bence kaldırma kuvveti bütün maddelerde vardır katılarda dahil. Ve olctugumuz tüm ağırlıklar sıfır olması dengenin sağlandığını gösterir. Mesele suyun içinde suyu ölmek 0 verir tropesferde aynı havayı olcmek sıfırdır ama hidrojen yada taş ölçmek farklı sonuç verir. Yani bir yerçekimi kuvveti vardır ve bu kuvvete göre ger maddenin bulunması gereken bir katman vardır doğru yerde ise ağırlık sıfır demektir yanlış yerde ise ya kaldırma kuvveti etki eder yada yer çekim kuvveti etki eder doğru yere gitmesi için. Yer altındaki suları yer üstüne çıkaran kuvvet ne kuvveti mesela yağmur un aşağı düşmesi de yukarı bulut olarak çıkmasında bu denge durumuyla alakalı. Bilmem doğrumu düşünüyorum.