Sürtünme ve Enerjinin Korunumu Örnek Sorular

Mekanik enerjinin sürtünme olmadığı zaman korunduğunu öğrenmiştiniz. Peki sürtünme olduğunda mekanik enerji korunur mu? Ya toplam enerji? Aslında bu konuyu daha önce 9. sınıfta öğrenmiştiniz ama unutmuş olabilirsiniz, enerjinin korunumu yazısını isterseniz bir gözden geçirin. Kısaca özetleyelim. Sürtünme olduğu zaman, sürtünme kuvveti sistem üzerinde negatif iş yapar, bu nedenle mekanik enerji, yani kinetik ve potansiyel enerjiler toplamı korunmaz. Ama kapalı bir sistemde toplam enerji yani mekanik enerji artı sistemin iç enerjisi korunur. Bunu bir örnekle açıklayalım.

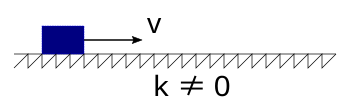
Şekildeki cisim v hızıyla sürtünmeli yatay düzlemde fırlatılmış. Sürtünme olduğu için bir süre sonra bu cisim durur. Yani ilk kinetik enerjisi son kinetik enerjisine eşit olmaz, potansiyel enerji de kazanmaz. Dolayısıyla mekanik enerjisi korunmaz. Çünkü sürtünme kuvveti negatif iş yapar. W= -F_sx. Ancak sistemi yüzey ve cisim olarak alırsanız, sürtünme kuvvetinin yaptığı işin yüzeyin ve cismin sıcaklıklarını artırdığını görürüz. Yani bu durumda sistemdeki toplam enerji korunur. Başlangıçtaki kinetik enerji yüzeyin ve cismin iç enerjisine dönüşür. Soru çözerek devam edelim.

Örnek soru 1

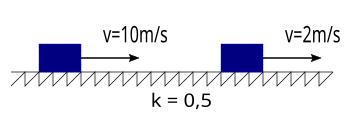
Şekilde gösterilen 4 kg kütleli bir cisim kinetik sürtünme katsayısı 0,5 olan yatay düzlemde hareket etmektedir. Cismin başlangıç hızı 10m/s’dir. Hızı 2m/s olunca cisim başlangıç konumuna göre kaç metre yer değiştirmiş olur?

Çözüm

Mekanik enerji korunmuyor ama toplam enerji korunuyor.

E_Toplam = E₁ = E₂ + F_sx

F_S = mgk = 4.(10).0,5 = 20 N
\frac{1}{2}mv_1^2 = \frac{1}{2}mv_2^2 + F_sx

\frac{1}{2}mv_1^2 = \frac{1}{2}mv_2^2 + F_sx \frac{1}{2}4(10)^2 = \frac{1}{2}4(2)^2 + 20x 200 J = 8 J + 20x 20x = 200J - 8J = 192J x = \frac{192}{20} = 9,6 m

Örnek soru 2

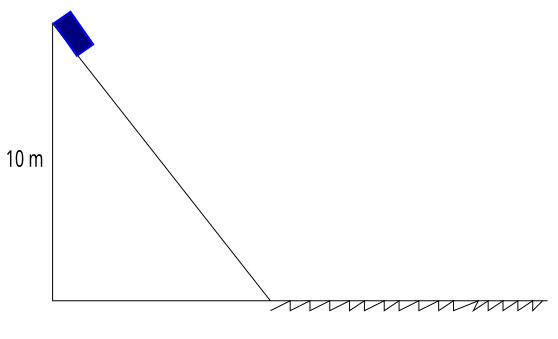
Şekildeki sürtünmesiz eğik düzlemin tepe noktasından m kütleli cisim serbest bırakılıyor. Cisim sonra kinetik sürtünme katsayısı 0,5 olan yatay düzlemde ilerlemeye başlıyor. (a) Cisim yatay düzlemde 5 m yol aldığında hızı kaç m/s olur? (b) Cisim yatay düzlemde kaç metre yol aldıktan sonra durur?

Çözüm

Tekrar hatırlayalım. Mekanik enerji korunmuyor ama toplam enerji korunuyor.

(a) Başlangıç enerjisi son enerjiye eşit olmalı.

E_Toplam = E₁ = E₂ + F_sx

Başlangıçta sadece potansiyel enerji var.

E₁ = mgh = (10 kg)(10 metre)m = 100m

Sürtünme kuvveti:

F_x = kmg = (0,5)(10)m = 5m

Sürtünme kuvvetinin yaptığı iş:

W = 5m(5 metre) = 25m

Son durumda kinetik enerji ve sürtünmenin yaptığı iş var.
E_2 = \frac{1}{2}mv^2 + Fx = \frac{1}{2}mv^2 + 25m
İki durumu birbirine eşitleyelim:
100 m = \frac{1}{2}mv^2 + 25m

100m - 25m = \frac{1}{2}mv^2 75m = \frac{1}{2}mv^2

v^2 = 150
v = \sqrt{150} = 12,25 m/s

(b) Bu daha kolay. Cismin sonunda durduğunu biliyoruz. Başlangıç enerjisi son enerjiye eşit olmalı.

E₁ = + F_sx
mgh = F_sx
Sürtünme kuvvetini bulmuştuk:
100 m = 5 mx

x = \frac{100}{5} = 20 metre

Örnek soru 3

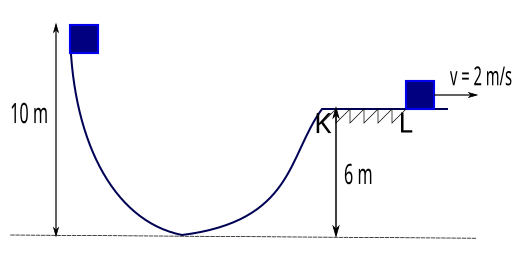
Düşey kesiti şekilde gösterilen yolda 4 kg kütleli bir cisim serbest bırakılıyor. Yolun sadece KL arası sürtünmelidir. Cisim L noktasından 2 m/s büyüklüğünde hızla geçtiğine göre hareket süresince ısıya dönüşen enerji kaç J olur?

Çözüm

Soru gözünüzü korkutmasın. Hep yaptığımızı yapacağız. Mekanik enerji korunmasa da toplam enerji korunuyor. İlk enerjiyi son enerjiye eşitleyeceğiz.

E₁ = E₂

E₁ = mgh = (4)(10)(10) = 400 J

L noktasına gelene kadar cisim hem 6 m tırmandı hem de sürtünmeli yolda ilerledi. Sürtünmenin yaptığı işe W_s diyelim:
E_2 = mgh_2 + W_s + \frac{1}{2}mv^2

E_2 = 4(10)(6) J + W_s + \frac{1}{2}4(2)^2 E_2 = 240 J + W_s + 8 J = 248 J + W_s

Şimdi eşitleyelim:
400 J = 248J + W_s

W_s = 400J - 248 J = 152 J

Sürtünme ve Enerjinin Korunumu ile ilgili simülasyon

Enerji kaykay parkı temel ilkeler PHET simülasyonu sürtünmeli durumlarda enerjinin korunumunu görselleştirmek için çok kullanışlı bir araç. Kurcalamanızı tavsiye ederim.

Sürtünme ve Enerjinin Korunumu ile ilgili kazanımlar

11.1.6.3. Sürtünmeli yüzeylerde enerji korunumunu ve dönüşümlerini analiz eder.

• Sürtünmeli yüzeylerde hareket eden cisimlerle ilgili enerji korunumu ve dönüşümü ile ilgili matematiksel hesaplamalar yapılması sağlanır.