Vektörlerde Toplama ve Çıkarma: Bileşke vektör

Vektörlerin yönü olduğu için iki vektörü, iki skaleri topladığımız gibi toplayamayız. Vektörlerde toplama ve çıkarma işlemlerini geometrik işlemlerle yapmamız gerekir. Vektör toplamada ya da çıkarmada sonuçta elde edilen vektöre bileşke vektör denir.

Uç uca Ekleme Yöntemi ile Vektörlerde Toplama ve Çıkarma İşlemi

Geometrik olarak iki vektörü toplamanın bir yolu vektörleri uç uca eklemektir:

• Birinci vektörün bitiş noktasına (yani okun ucuna), diğer vektörün başlangıç noktası taşınır. (Vektörler taşınabilir.)
• Birinci vektörün başlangıç noktasıyla ikinci vektörün bitiş noktası birleştirilir ve yeni bir vektör çizilir. Bu yeni vektör iki vektörün toplamı yani bileşkesidir, \vec{R} ile gösterilir.
• Vektörler toplanırken işlem sırası önemli değildir. Vektörel toplama işlemi değişme özelliğine sahiptir.

\vec{A} + \vec{B} = \vec{B} + \vec{A} = \vec{R}

Aynı doğrultudaki vektörlerde toplama ve çıkarma

Eğer iki ya da daha fazla vektör aynı doğrultudaysa (birbirine paralelse) toplama işlemi kolaydır. Vektörler uçuca eklenir ve büyüklükleri toplanır.

Aşağıdaki resimde +x yönündeki (sağa doğru) 3 birim kare uzunluğundaki \vec{A} vektörüyle yine +x yönündeki 4 birim kare uzunluğundaki \vec{B} vektörünün toplanması gösteriliyor. Bileşke vektör \vec{R} ile gösteriliyor ve uzunluğu 7 birim kare ve yönü de +x.

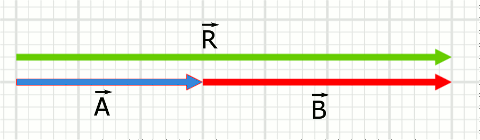
\vec{A}+\vec{B} = \vec{R} : İki vektörün vektörel toplamı böyle gösterilir.

|\vec{R}| = |\vec{A} + \vec{B}| : İki vektörün büyüklüklerinin toplamı da aynı doğrultudalarsa mutlak değerlerinin toplamıyla gösterilir.

|\vec{R}| = |3 + 4| = 7 \space birim

Aynı doğrultudaki iki vektörün çıkarma işlemi de basittir. Çıkarma işleminin anlamını düşünmek gerekir. Çıkarma işlemi çıkarılan sayıyı -1 ile çarpıp, çıkan sayıyla toplamak demektir. Yani:

A - B = A +((-1)B)

Vektörlerde -1 ile çarpmanın vektörün yönünün değiştirilmesi anlamına geldiğini öğrenmiştik. Öyleyse \vec{A}-\vec{B} = \vec{A} + (-\vec{B}) şeklinde çıkarma işlemini yapabiliriz. Bu durumda \vec{B} vektörünün yönünü değiştirip \vec{A} vektörüyle toplarız. Aşağıdaki resim bu çıkarma işlemini gösteriyor.

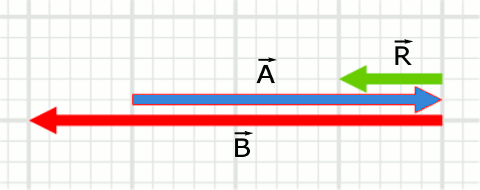
\vec{A}-\vec{B} = \vec{R} iki vektörün vektörel çıkarılması böyle gösterilir.

|\vec{R}| = |\vec{A} - \vec{B}| İki vektörün büyüklüklerinin çıkarılması da aynı doğrultudalarsa mutlak değerlerinin çıkarılmasıyla gösterilir.

|\vec{R}| = |3 - 4| = 1 \space birim

Bileşke vektörün uzunluğu +1 birim kare, ama yönü -x’e doğru. Bu nedenle \vec{R} = -1, eksi işareti yönünün -x’e doğru olduğu anlamına geliyor.

Farklı doğrultudaki vektörlerde toplama ve çıkarma

Aşağıdaki resimdeki \vec{A} ve \vec{B} vektörlerini uç uca ekleyerek toplayacağız. Bu resim vektörlerin toplanmamış halini gösteriyor.

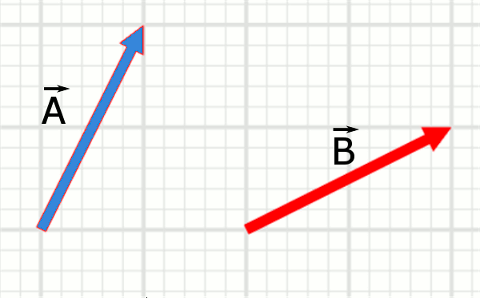
\vec{A} vektörünün ucuna \vec{B} vektörünü ekleyince şöyle görünüyor ve bileşke vektör \vec{R} oluyor.

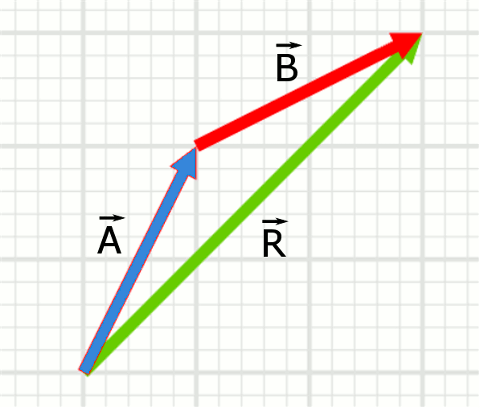Toplama işleminde işlem sırasının önemsiz olduğunu da aşağıdaki şekilde görebiliyoruz. \vec{B} vektörünün ucuna \vec{A} vektörünü ekleyince bileşke vektör \vec{R} değişmiyor.
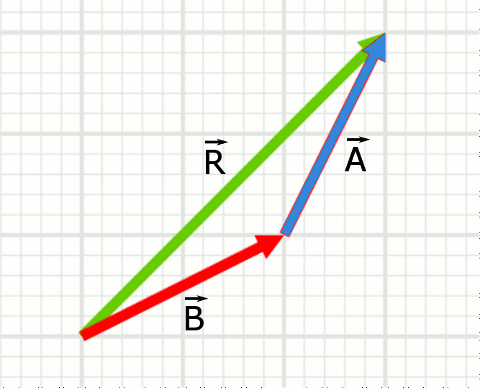Vektörleri taşırken yönlerini ve büyüklüklerini koruduğumuza dikkat etmelisiniz.

Örnek soru çözümü 1: Uç uca eklenen 3 vektör

 

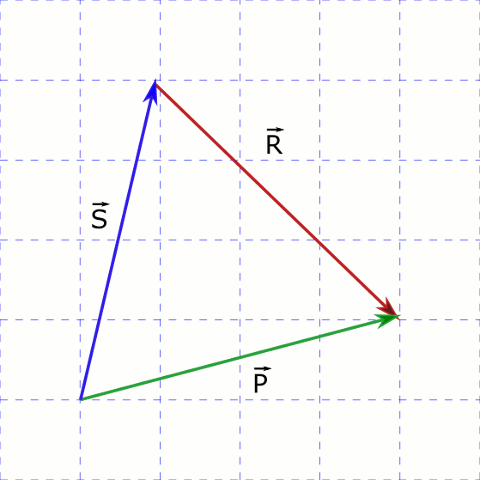
Yukarıdaki şekilde gösterilen üç vektörün toplamı kaç \vec{P}‘dir?

Çözüm:

Şekilde dikkat etmeniz gereken uç uca toplama yönteminde bir vektörün ucunun diğer vektörün başlangıç noktasına gelmesi. Yalnızca \vec{S} ile \vec{R} bunu sağlıyor. Ama ne \vec{S} ile \vec{P} (ikisinin de başlangıç noktaları uç uca gelmiş) ne de \vec{S} ile \vec{R} (ikisinin de bitiş noktaları uç uca gelmiş) bunu sağlamıyor.

\vec{S}+ \vec{R} = \vec{P}

Bizden \vec{S} + \vec{R} + \vec{P} isteniyor. Vektörlerde toplama işlemi birleşme özelliğine de sahiptir. Yani:

\vec{S} + \vec{R} + \vec{P} = (\vec{S} + \vec{R}) + \vec{P} = \vec{P} + \vec{P} = 2\vec{P}

Örnek soru çözümü 2: İki vektörün çıkarılması

Bir önceki sorudaki şekilde \vec{P} - \vec{R} işleminin sonucu nedir?

Çözüm:

Çıkarma işleminin çıkarılan vektörün negatifiyle toplama olduğunu biliyoruz. Yani:

\vec{P} - \vec{R} = \vec{P} + (-\vec{R})

-\vec{R} vektörü \vec{R} vektörünün zıttı olduğuna göre yönünü ters çevirip \vec{P} ile toplayabiliriz.

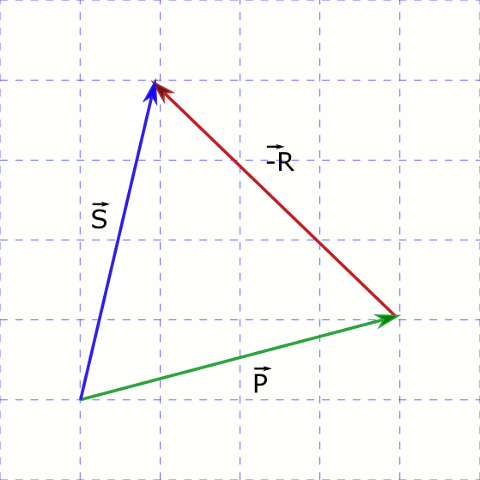
\vec{P} + (-\vec{R}) = \vec{S} olduğu yukarıdaki şekilde görülüyor.

Örnek soru çözümü 3: Başladığı yerde biten vektörler

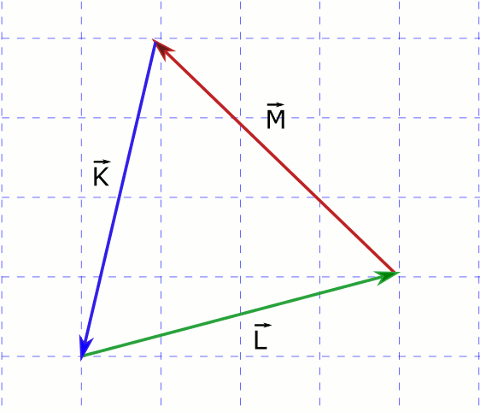
Yukarıdaki şekilde verilen vektörlere göre, bileşke vektör \vec{K}+\vec{L}+\vec{M} nedir?

Çözüm:

Uç uca ekleme metodunda K’nın ucuna L’yi ekleyince \vec{-M} elde ediliyor. \vec{M}+\vec{-M} = 0. Yani toplanan vektörlerin ilkinin başlangıç noktasıyla sonuncusunun bitiş noktası kesişiyorsa bu vektörlerin bileşkesi sıfırdır.

Paralel Kenar Yöntemi ile Vektör Toplama ve Çıkarma

Vektörleri toplamanın bir başka yolu da pararlel kenar yöntemidir:

• Toplanacak olan iki vektörün başlangıç noktaları aynı noktaya taşınır.
• Birinci vektörün bitiş noktasından ikinci vektöre paralel bir çizgi çizilir; ikinci vektörün bitiş noktasından da birinci vektöre paralel bir çizgi çizilir. Böylece oluşan şekil bir paralel kenara tamamlanır.
• Vektörlerin başlangıç noktasıyla paralel kenarın karşısındaki köşesini birleştiren köşegene bileşke vektör çizilir. Bileşke vektörün başlangıç noktası, toplanan vektörlerin başlangıç noktasıyla aynıdır.

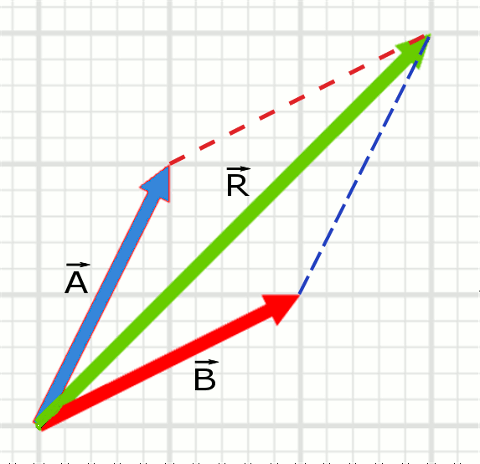
Aşağıdaki resimdeki \vec{A} ve \vec{B} vektörlerini paralel kenar yöntemini kullanarak toplayacağız. Bu resim vektörlerin toplanmamış halini gösteriyor.

İki vektörün başlangıç noktalarını aynı noktaya taşıyıp, şekli paralel kenara tamamlayıp, köşegene de bileşke vektörü çiziyoruz.

Kosinüs Teoremi

Paralel kenar yöntemiyle topladığımız iki vektörün bileşkesini çizebiliyoruz. Peki büyüklüğünü nasıl buluruz? Bunun için geometriden kosinüs teoremini kullanıyoruz.

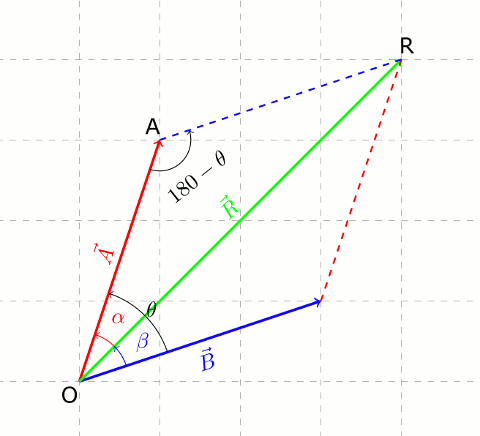
Yukarıdaki şekildeki OAR üçgeninde, OAR açısının 180 – θ olduğunu görüyoruz. Kosinüs teoremi A ve B kenarlarının uzunluklarıyla R kenarının hesaplanabileceğini anlatır.

R^2 = A^2 + B^2 - 2ABcos(180-\theta)

Trigonometriden bildiğiniz gibi:

cos(180 - \theta) = -cos\theta

Öyleyse kosinüs teoremi şu hale gelir:

R^2 = A^2 + B^2 + 2ABcos\theta

\vec{A} ile \vec{R} arasındaki açı \alpha, \vec{B} ile \vec{R} arasındaki açı \beta olsun:

• |\vec{A}| = |\vec{B}| ise \alpha = \beta
• |\vec{A}| > |\vec{B}| ise \alpha < \beta
• |\vec{A}| < |\vec{B}| ise \alpha > \beta olur.

Özel durumlar:

• θ = 90° olduğunda cos 90° = 0 olduğu için 2ABcos(90°) = 0 olur. Kosinüs teoremi Pisagor teoremine dönüşür:
  R^2 = A^2 + B^2
• \theta = 0^\circ olduğunda cos(0^\circ) = 1 olduğu için 2ABcos(0^\circ) = 2AB olur. Aynı yönlü iki kuvvetin toplamının ispatı böyle yapılabilir:
  R^2 = A^2 + B^2 + 2ABcos(0^\circ)
  R^2 = A^2 + 2AB + B^2 = (A+B)^2
  \sqrt{R^2} = \sqrt{(A+B)^2}
  |R| = |A+B| = |A|+|B|
• \theta = 180^\circ olduğunda cos(180^\circ) = -1 olduğu için 2ABcos(180^\circ) = -2AB olur. Zıt yönlü iki kuvvetin toplamının ispatı böyle yapılabilir:
  R^2 = A^2 + B^2 + 2ABcos(180^\circ)
  R^2 = A^2 - 2AB + B^2 = (A-B)^2
  \sqrt{R^2} = \sqrt{(A-B)^2}
  |R| = |A-B|

Örnek soru çözümü 3:

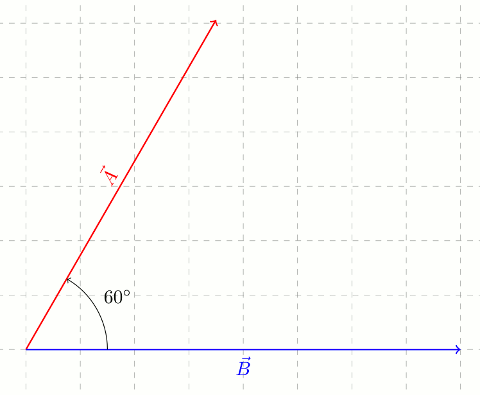
Yukarıdaki şekilde verilen \vec{A} vektörünün uzunluğu 7 birim, \vec{B} vektörünün uzunluğu 8 birimdir ve iki vektör arasındaki açı 60^\circ‘dir. \vec{A}+\vec{B} vektörünü çiziniz ve uzunluğunu hesaplayınız.

Çözüm:

Paralel kenar yöntemiyle bileşke vektörü çizebiliriz:

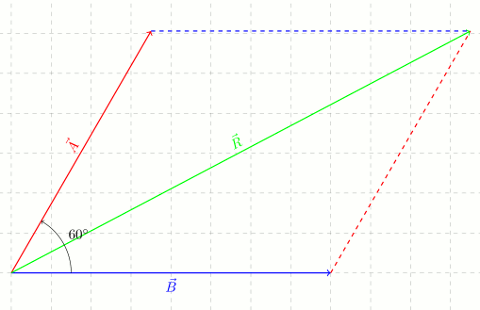
Bileşke vektörün uzunluğunu da kosinüs teoreminden bulabiliriz:

R^2 = A^2 + B^2 + 2ABcos60^\circ R^2 = 49+64+2(7)(8)(0,5) R^2 = 169 \sqrt{R^2} = \sqrt{169} R = 13 \space birim

Eşit büyüklükteki vektörlerde toplama için özel açılar

Toplanan iki vektörün büyüklüğü eşit ise bazı açılarda hesaplamaların hızlı yapılması mümkündür.

|\vec{A}|=|\vec{B}| = A ise:

• \theta = 0^\circ olduğunda: R = 2A (Aynı yönlü, eşit vektörler.)
• \theta = 60^\circ olduğunda: R = A\sqrt{3} (Kosinüs teoreminden ispatını yapabilirsiniz)
• \theta=90^\circolduğunda: R=A\sqrt{2} (Pisagor teoreminden ispatını yapabilirsiniz.)
• \theta = 120^\circ olduğunda: R = A (Kosinüs teoreminden ispatını yapabilirsiniz)
• \theta = 180^\circ olduğunda: R = 0 (Zıt yönlü, zıt vektörler.)

Vektörler Test

Vektörler konusunu ne kadar iyi öğrendiğinizi sınamak için Vektörler Testini yapabilirsiniz.

Vektörlerde Toplama ve Çıkarma ile ilgili Simülasyon

Uç uca ekleme ve paralel kenar yöntemleriyle vektörlerde toplama ve çıkarma yapabileceğiniz şu simülasyona bakabilirsiniz: Vektör Toplama PHET Simülasyonu

Vektör Toplama ve Çıkarma Video

Özellikle animasyonlar vektörleri gözünüzde canlandırmayı kolaylaştırabilir.

Vektörlerde Toplama ve Çıkarma ile ilgili Fizik Dersi Kazanımları

11.1.1.3. Vektörlerin bileşkelerini farklı yöntemleri kullanarak hesaplar.

• Uç uca ekleme ve paralel kenar yöntemleri kullanılmalıdır.
• Kosinüs teoremi verilerek bileşke vektörünün büyüklüğünün bulunması sağlanır.
• Eşit büyüklükteki vektörlerin bileşkesi hesaplanırken açılara göre özel durumlar verilir.