Şimdiye kadar, pillerin ve diğer üreteçlerin direnci olmayan malzemelerden üretildiğini, bu nedenle iç dirençleri olmayan, ideal piller ya da üreteçler olduğunu varsaymıştık. Ama ideal diye bir şey gerçek hayatta yoktur, gerçek piller ve üreteçler direnci olan malzemelerden üretilir. Bu yüzden de pillerin kendilerine özgü dirençleri vardır, buna iç direnç denir. İç direnç bir pilin devreye sağladığı potansiyel farkı sınırlar. Bu nedenle piller ve üreteçler saf voltaj (gerilim veya potansiyel fark) kaynakları değildir. Bir pilin ya da üretecin devreye sağladığı net potansiyel farkına elektromotor kuvvet veya EMK denir. EMK elektronları (daha genel olarak yük taşıyıcılarını) hareket ettiren kuvvet anlamına gelse de, aslında bir kuvvet değildir, potansiyel farktır. Kuvvet olsaydı biriminin Newton olması gerekirdi, oysa EMK’nın birimi volttur. Çünkü EMK birim yükün devrede taşınması için gereken enerjiye ya da yapılan işe oranıdır (ε=W/q). Şimdiye kadar pillerin potansiyel farkını temsil etmek için V yazıyorduk, artık EMK’nın simgesi olan ε (epsilon)’nu kullanacağız.
İçdirenci olan gerçek bir pil, bir voltaj kaynağı ve buna seri bağlı bir direnç şeklinde modellenir. Aşağıdaki resimde devre yapım seti simülasyonu kullanarak bir pilin nasıl modellendiği gösteriliyor. Pilin devreye sağladığı gerilimi EMK (ε), iç direncini r ile gösteriyoruz.
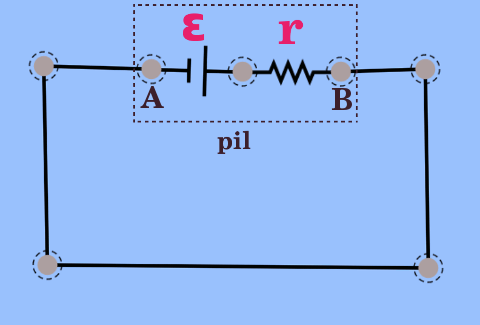
Kesikli çizgilerle gösterilen bölge pili temsil ediyor; A ve B noktaları da pilin iki ucunu. Bu durumda, pilin uçları (A ve B noktaları) arasındaki gerilim (voltaj veya potansiyel fark) Kirchoff Kanunlarına ve Ohm Kanunu’na göre şöyle bulunur:
VAB = ε – Ir
V pilin uçları arasındaki potansiyel farkı, ε pilin EMK’sını (devreye sağladığı saf potansiyel farkı), r pilin iç direncini, I da devreden geçen akımı gösteriyor. Bu formül, pilin EMK’sı ile uçları arasındaki potansiyel fark arasındaki ilişkidir.
Şimdi bu ilişkiyi yorumlayalım. Genellikle bir pilin EMK’sının sabit olduğunu düşünürüz, çünkü EMK sadece pilin içinde gerçekleşen, kimyasal enerjiyi elektrik enerjisine dönüştüren tepkimelere bağlıdır. Ama pilin uçları arasındaki potansiyel farkın (pilin voltajının) akım arttıkça azaldığına dikkat etmelisiniz. Pilin gerilimi yalnızca akım ihmal edilebilecek kadar küçük olduğunda EMK’ya eşit olur:
I = 0
VAB = ε – 0r = ε
Normal koşullarda pilin devreye sağlayabileceği maksimum (azami) akım şu kritik değeri geçemez:
I0 = ε/r
Gerçek pilleri tanımlamak için devreye sağladıkları EMK (ε, yani akım sıfırken devreye sağladığı potansiyel fark) ve maksimum akım (I0 ) kullanılır. Örneğin, standart kuru piller (kalem pil gibi) 1,5 V ve 0,1 A olarak sınıflanır. Bu değerler küçük olduğu için eğer bir kalem pili kısa devre yaparsanız (direnç bağlamadan sadece telle uçlarını birleştirirseniz, yukarıdaki resimdeki gibi) bir felaketle karşılaşmazsınız. Ama bir araba aküsü 12 V ve 200 A olarak sınıflandırılır. Araba aküsünün iç direnci kuru pile göre daha düşüktür. Akımın 200 A olması motoru çalıştırabilmek için gereklidir. Bu kadar yüksek akım, kısa devre durumunda çok tehlikelidir.
Şimdi de bu pili bir dirence bağlayıp bir elektrik devresi kurduğumuz durumu inceleyelim. Aşağıdaki resimde bu durum gösteriliyor.
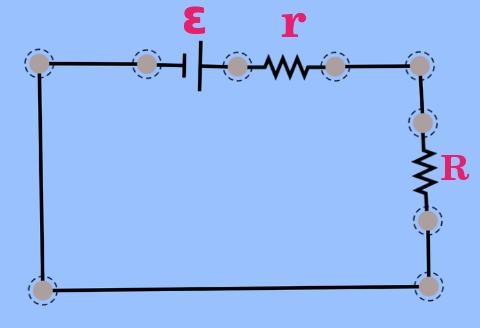
Bu devreyi analiz etmek için Kirchoff ve Ohm kanunlarını kullanabiliriz:
ε – Ir -IR = 0
ε = I(r+R)
Bir pilin bitmesi demek iç direncinin artması anlamına gelir. İç direnci artan pil bir devreye bağlandığında devreye yeterli gücü sağlayamayacak hale gelir. Bitmiş bir pile voltmetre bağlayıp pilin uçları arasındaki gerilimi ölçerseniz, neredeyse bitmemiş bir pille aynı voltaja sahip olduğunu görürsünüz. Bu nedenle bir pilin bitip bitmediğini anlamak için voltmetre kullanışlı bir araç değildir. Ama bitmiş pili bir devreye bağlarsanız geriliminin düştüğünü görürsünüz. Bunun nedeni iç direncin gerilimi düşürmesidir, bu nedenle pilin dışarıdaki devreye sağlayabileceği potansiyel fark çok azalır.
EMK ve İç Direnç ile ilgili Örnek Soru
İç direnci 4 Ω elektromotor kuvveti (emk) 21 V olan üreteçle aşağıdaki şekildeki elektrik devresi kuruluyor. Anahtar kapatıldıktan sonra voltmetre ve ampermetre hangi değerleri gösterir?
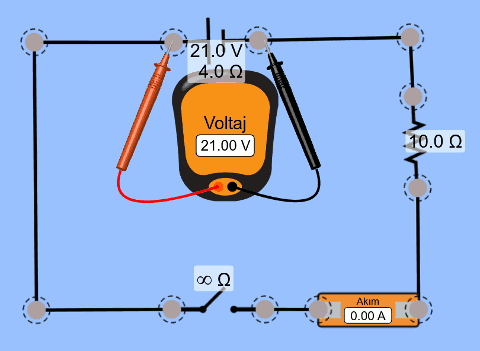
Çözüm:
Anahtar açıkken direncinin sonsuz olduğuna dikkat edin. Sonsuz dirençli bir devreden elektrik akımı geçemez. Bu sırada voltmetre, devreden akım geçmediği için, pilin uçları arasındaki farkın EMK’ya eşit olduğunu gösteriyor. Ama anahtar kapatılınca, anahtar sadece bir tel olduğu için, direnci sıfır oluyor. Anahtar kapatıldığı anda devreden bir akım geçecek. Bu devrede iç direnç devreye seri bağlı sıradan bir direnç gibi davranıyor. Öyleyse Kirchoff’un döngü (voltaj) kanununu yazarsak:
ε – Ir -IR = 0
ε = I(r+R)
Şimdi değerleri yerine koyalım. Devrede yalnızca bir üreteç var.
21 V = I(4 Ω + 10 Ω)
I = 21 V / 14 Ω = 1,5 A
Akımı bulduk, ampermetre akımın değerini yani 1,5 A gösteriyor. Şimdi de pilin uçları arasındaki potansiyel farkı bulalım.
VAB = ε – Ir
VAB = 21 V – (1,5 A) (4 Ω)
VAB = 21 V – 6 V = 15 V
Voltmetre pilin uçlarına bağlandığı için, devreden akım geçmeye başladığı anda 15 V değerini gösterecek. Gördüğünüz gibi pilin uçları arasındaki gerilim pilin EMK’sından daha düşük çıktı. Bir de simülasyonun sonuçlarını gösterelim. Aşağıdaki şekli bir inceleyin.
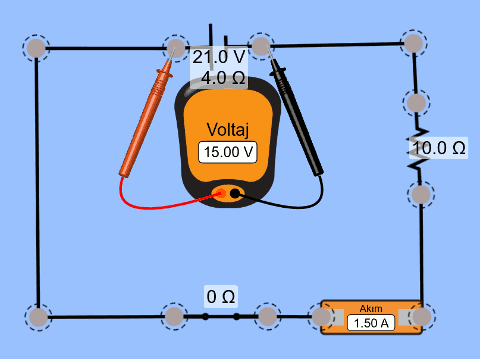
Gerçekten de voltmetrenin 15 V, ampermetrenin 1,5 A okuduğunu görüyoruz.
EMK ve İç Direnç ile ilgili kazanımlar
2017 – 10.1.2.2. Üreteçlerin seri ve paralel bağlanma gerekçelerini açıklar.
- Üreteçlerin iç dirençleri örneklerle açıklanır, iç dirençler ile ilgili matematiksel hesaplamalara girilmez.