Mekanik Enerjinin Korunumu: Örnek soru çözümleri

Mekanik enerjinin bir cismin ya da sistemin kinetik enerjisi ile potansiyel enerjisinin toplamı olduğunu öğrenmiştiniz. Mekanik enerjinin korunumu da, sürtünmenin olmadığı durumlarda cismin hareketi boyunca toplam mekanik enerji değerinin sabit olduğu anlamına geliyor. Yani bir cismin kinetik enerjisi ve potansiyel enerjisi, cisim hareket ediyorsa zamana göre değişebilir, ama bu ikisinin toplamı yani mekanik enerji değişmez. Enerjinin korunumu yasasını gözden geçirmek isteyebilirsiniz. Artık 11. sınıf olduğunuza göre matematiksel uygulamalı örnek soruları çözmeniz bekleniyor. Bu yazıda çeşitli örnek sorular çözeceğiz.

Mekanik enerji ve serbest düşme

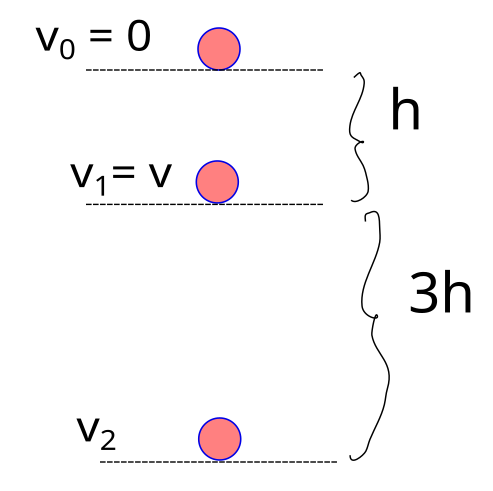
Şekildeki cisim sürtünmelerin ihmal edildiği ortamda serbest düşmeye bırakılmıştır. Cisim h yüksekliği kadar düştüğü anda hızı v olmaktadır. Buna göre cisim 3h yükseklik daha düşerse hızı kaç v olur?

Çözüm

Cismin kesikli çizgilerle gösterilen noktalardaki kinetik ve potansiyel enerjilerini bulabiliriz. Kinetik ve potansiyel enerji toplamının yani mekanik enerjisinin her noktada aynı olması gerekiyor.
E_0 = K + P = 0 +mg(4h)
İkinci noktada:
E_1 = \frac{1}{2}mv^2+mg(3h)
Yere çarptığında:
E_2 = \frac{1}{2}mv_2^2+0
Bu üç noktada mekanik enerji birbirine eşit yani:
E_0 = E_1 = E_2
İlk iki eşitlikten:
4mgh = 3mgh+\frac{1}{2}mv^2

mgh = \frac{1}{2}mv^2

Hızı yükseklik (h) cinsinden bulabiliriz:
v = \sqrt{2gh}
Başangıç ve son nokta eşitliğinden:
\frac{1}{2}mv_2^2 = 4mgh

v_2 = 2\sqrt{2gh} = 2v

Mekanik enerji ve atışlar

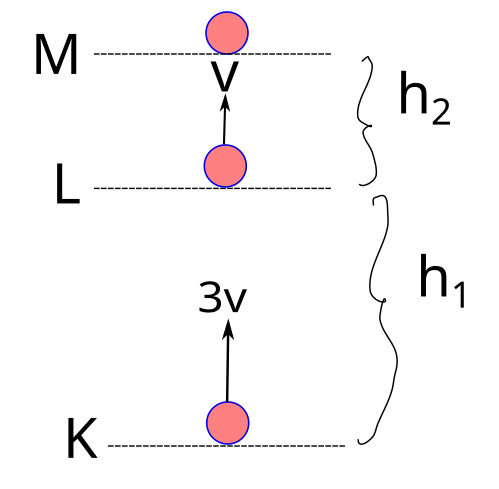
Şekildeki cisim sürtünmelerin ihmal edildiği ortamda K noktasından yukarı doğru dik olarak 3v hızıyla atılmıştır. Cisim L noktasına geldiğinde hızı v olmakta, M noktasına geldiğinde ise cisim durmaktadır. K-L arası yükseklik h₁ ve L-M arası yükseklik h₂ olduğuna göre, h₁/h₂ oranı kaçtır?

Çözüm

Cismin mekanik enerjisi hareketi boyunca korunur, yani K, L ve M noktalarında kinetik ve potansiyel enerjisinin toplamı eşittir.
E_K = E_L = E_M
K noktasında yalnızca kinetik enerjisi var çünkü yüksekliği sıfır.
E_K = \frac{1}{2}m(3v)^2 = \frac{1}{2}m9v^2
M noktasında ise cismin kinetik enerjisi sıfır, mekanik enerjisinin tümü potansiyel enerjisinden geliyor:
E_M = mg(h_1+h_2)
Bu iki noktadaki mekanik enerji birbirine eşit:
mg(h_1+ h_2) = \frac{9}{2}mv^2
v’yi h₁ ve h₂ toplamı cinsinden yazabiliriz:

v^2 = \frac{2}{9}g(h_1 + h_2)
Şimdi de L ve M noktalarındaki mekanik enerjiyi eşitleyelim:
mg(h_1+h_2) = mgh_1 +\frac{1}{2}mv^2

mgh_2 = \frac{1}{2}mv^2 v^2 = 2gh_1

Artık hızların karelerini birbirine eşitleyebiliriz:
v^2 =\frac{2}{9}g(h_1 + h_2) = 2gh_2
Buradan:
h_1 + h_2 = 9h_2

h_1 = 8h_2

Öyleyse:
\frac{h_1}{h_2} = \frac{8h_2}{h_2} = 8

Mekanik enerji ve eğik düzlem

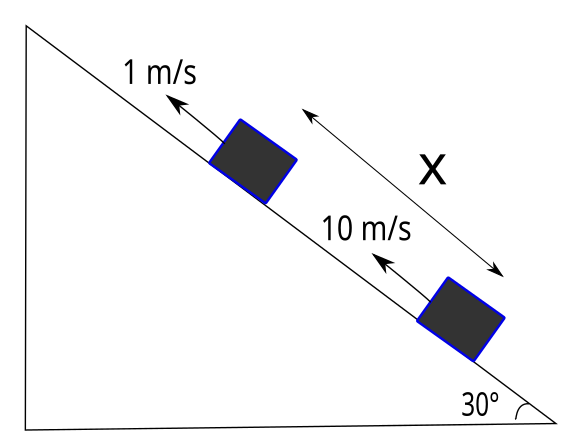
Sürtünmelerin ihmal edildiği eğik düzlemde 4 kg kütleli bir cisim 10 m/s süratle yukarı yönde fırlatılıyor. Cisim x metre yer değiştirdiği anda

sürati 1 m/s oluyor. Buna göre cismin x yer değiştirmesi kaç metredir?

Çözüm

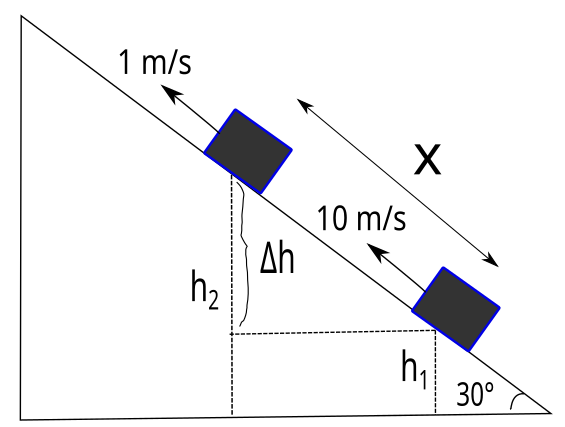
Cismin başlangıç ve bitiş konumlarındaki mekanik enerjisinin aynı olduğunu biliyoruz. Eğik düzlemin alt noktasında cismin yüksekliğine h₁ diyelim. Üst noktasındaki yüksekliğine de h₂ diyelim.

Δh =x (sin 30°) = (h₂ – h₁) = x sin 30° olur.

Cismin birinci konumundaki enerjisi:
E_1 = \frac{1}{2}4(10)^2 + 4(10)h_1= 200 J + 40h_1
İkinci konumdaki enerjisi:
E_2 = \frac{1}{2}4(1)^2 + 4(10)h_2 = 2J+40h_2
Buradan iki mekanik enerjiyi eşitleyelim:
200 J + 40h_1 = 2J + 40h_2

40(h_2 - h_1) = (200-2)J = 198J

Şimdi yükseklikler arasındaki farkı bulalım:
\Delta h = h_2 - h_1 = \frac{198}{40} = 4,95 m
Şimdi x’i bulabiliriz.
x sin 30^\circ = \Delta h

x = \Delta h\frac{1}{sin30^\circ} = 4,95(2) = 9m

Mekanik enerji ve sarkaç

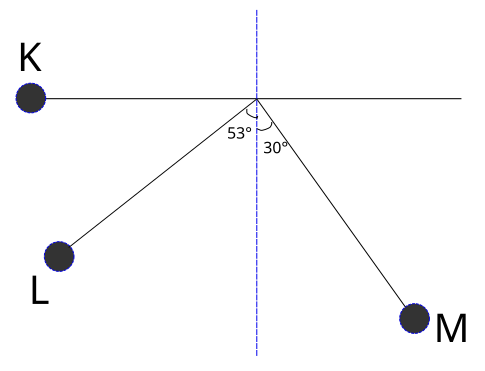
Şekilde gösterilen sürtünmelerin ihmal edildiği sistemde ağırlıksız bir çubuğa bağlı m kütleli bir cisim K noktasından serbest bırakılıyor. Cisim L noktasından v_L, M noktasından v_M büyüklüğünde hızlarla geçtiğine göre, v_L/v_M oranı kaçtır?

Çözüm

Şekli yükseklikleri gösterecek biçimde tekrar çizelim. Cismin denge konumuna göre L noktasının yüksekliğine h₁, M noktasının yüksekliğine h₂ diyelim.

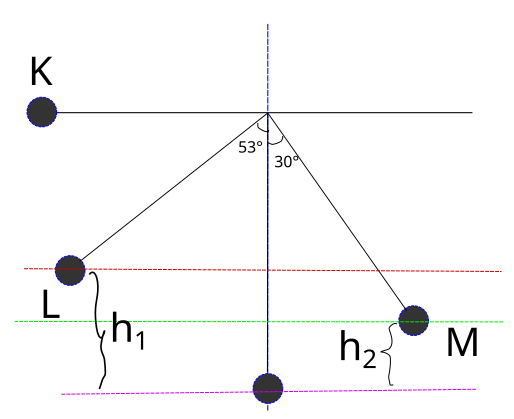
Çubuğun uzunluğunu kullanarak h₁ yüksekliğini bulabiliriz. Çubuğun uzunluğuna l diyelim,l soldaki dik üçgenin hipotenüsüne eşit.
l (cos 53^\circ) = l - h_1

0,6l = l-h_1 h_1 = l - 0,6l = 0,4 l

Aynı şekilde h₂ yüksekliğini de bulabiliriz. l sağdaki dik üçgenin hipotenüsüne eşit.
l(cos30^\circ) = l - h_2

l\frac{\sqrt{3}}{2} = l - h_2 h_2 = l(1-\frac{\sqrt{3}}{2})

Şimdi K ve M noktaları için mekanik enerjinin korunumunu yazalım.
mgl = mgh_1+\frac{1}{2}mv_K^2

mgl = mg(0,4l)+\frac{1}{2}mv_K^2 0,6mgl = \frac{1}{2}mv_K^2 V_K = \sqrt{1,2gl}

Şimdi de K ve M noktaları için mekanik enerjileri eşitleyelim.
mgl = mgh_2+\frac{1}{2}mv_L^2

mgl = mgl(1-\frac{\sqrt{3}}{2})+\frac{1}{2}mv_L^2 mgl (1-1+\frac{\sqrt{3}}{2}) = \frac{1}{2}mv_L^2 V_L = \sqrt{gl\sqrt{3}} = \sqrt{1.73gl}

Artık oranı bulabiliriz:
\frac{V_K}{V_L}=\frac{\sqrt{1,2gl}}{\sqrt{1,73gl}}=0,83

Mekanik enerji ve yaylar

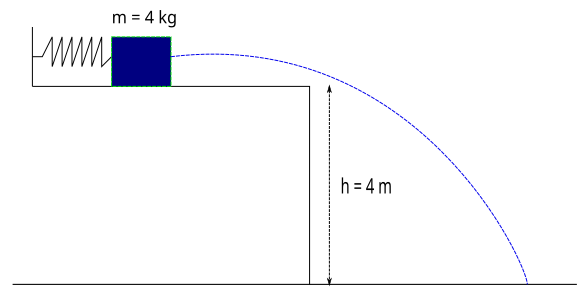
Sürtünmesi ihmal edilen yatay düzlemde yay sabiti 400 N/m olan bir yay 0,4 m sıkıştırılıp önüne 4 kg kütleli bir cisim yerleştiriliyor. Yay serbest bırakıldıktan sonra cisim 4 m yükseklikten şekildeki yörüngeyi izleyerek yere düşüyor. Buna göre takozun yere çarpma hızı kaç m/s olur?

Çözüm

İlk durumdaki mekanik enerji, son durumdaki mekanik enerjiye eşit olmak zorunda. İlk durumda yayda depolanan elastik potansiyel enerji ve yükseklikten kaynaklanan kütle çekim potansiyel enerjisi var, kinetik enerji yok çünkü başlangıçta cisim duruyor.
E_1 = \frac{1}{2}kx^2+mgh = \frac{1}{2}400(0,4)^2 + 4(10)4 = 32J+160J = 192J
Yere çarptığındaki durumda ise potansiyel enerji yok sadece kinetik enerji var.
E_2 = \frac{1}{2}mv^2 = \frac{1}{2}4v^2 = 2v^2

E_1 = E_2 192 J = 2v^2 v^2 = 96 v=9,8 m/s

Mekanik enerjinin korunumuyla ilgili simülasyon

Enerji kaykay parkı temel ilkeler PHET simülasyonu mekanik enerjinin korunumunu görselleştirmek için çok kullanışlı bir araç. İncelemenizi öneririm.

Mekanik enerjinin korunumuyla ilgili kazanımlar

11.1.6.2. Cisimlerin hareketini mekanik enerjinin korunumunu kullanarak analiz eder.

• Öğrencilerin serbest düşme, atış hareketleri ve esnek yay içeren olayları incelemeleri ve mekanik enerjinin korunumunu kullanarak matematiksel hesaplamalar yapmaları sağlanır.