Kütle Merkezi ve Ağırlık Merkezi nedir?

Kütle merkezi ve ağırlık merkezi kavramları ilk bakışta aynı şey gibi görünebilir. Bu iki kavram ilişkili olsalar da aynı şey değiller. Aralarındaki fark aslında kütle ile ağırlık arasındaki farktan kaynaklanıyor. Kütle bir cisimdeki madde miktarıdır. Ağırlık ise bir cisme kütlesinden dolayı uygulanan yerçekimi kuvvetidir. Bu nedenle kütleden bahsederken kilogram birimini, ağırlıktan bahsederken kuvvetin birimi olan Newton’u kullanırız. Şimdi sırayla bu merkez kavramlarını inceleyelim. Önce ağırlık merkezine bakalım.

Ağırlık merkezi nedir?

Fizikte cisimleri ve sistemleri incelerken genellikle bu cisimleri ve sistemleri oluşturan parçacıklarına ayırırız. Ağırlık merkezi bir cismi oluşturan parçacıkların ağırlıklarının bileşkesinin uygulama noktasına denir. Ancak yer çekimi olmayan ortamlarda cismin ağırlığı olmaz (g=0 ise mg=0), bu nedenle yerçekimsiz ortamda ağırlık merkezi kavramından da bahsedemeyiz. Ağırlık merkezi vektörel bir büyüklük olan ağırlığın uygulama merkezidir.

Henüz Newton’un Evrensel Kütleçekimi yasasını öğrenmediniz. Ama kısa bir fragman verelim. Kütlesi olan iki cisim birbirini çeker yani kuvvet uygular. Bu kuvvet şöyle gösterilir:
\vec{F} = G \frac{m_1m_2}{r^2}

G evrensel kütleçekim sabiti, m₁ ve m₂ iki cismin kütleleri, r ise cisimlerin merkezleri arasındaki uzaklıktır. Neden bu kanunu verdik? Uzaklığın karesine göre uygulanan kütleçekimi azalıyor, bunu göstermek için. Öyleyse bir cismin yerden ne kadar yüksekte olduğuna göre cisme uygulanan kütleçekim kuvveti (ağırlık yani) değişir. Cisim yere yakında kütleçekim kuvveti daha büyük, yerden yüksekteyse daha küçük olur. Bir de yerçekimi ivmesiyle ilişkilendirelim bunu:
\vec{F} = G \frac{m_Dm}{r^2}

m_D Dünya’nın kütlesi, m cismin kütlesi olsun. Şimdi g’yi yani yerçekimi ivmesini tanımlayacağız:
\vec{g} = G \frac{m_D}{r^2}

Dolayısıyla bir noktadaki yer çekimi ivmesi, o noktanın Dünya’nın merkezine olan uzaklığına göre değişir. Yerçekimi ivmesi (g) yeryüzüne yakın bir noktada yeryüzünden daha uzak bir noktaya göre daha fazladır. Küçük bir cisimden bahsediyorsak bir cismin altı ile üstü arasında büyük bir fark olmayabilir. Ama ya kocaman bir gökdelenden bahsediyorsak?

Yukarıdaki resimde Dubai’deki Burj Kalifa gökdeleni görülüyor. Bu gökdelenin yüksekliği 828 metre. Gelin gökdelenin en alt noktasında, tam ortasında ve en üst noktasında yerçekimi ivmesini hesaplayalım.

G = 6.674 x 10^-11 m³/kgs² (Evrensel kütleçekim sabiti)

m_D = 5.972 × 10²⁴ kg (Dünya’nın kütlesi)

r_D = 6378100 m (6378 km) (Dünyanın yarıçapı)

r_alt = r_D + 0 = 6378100 m

r_orta = r_D + (828/2) = 6378514 m

r_üst = r_D + 828 = 6378928 m
g_{alt} = 6.674 \times 10^{-11} \frac{m^3}{kgs^2} \frac{5.972 \times 10^{24} kg}{6378100^2 m^2} = 9.79768 \space m/s^2

g_{orta} = 6.674 \times 10^{-11} \frac{m^3}{kgs^2} \frac{5.972 \times 10^{24} kg}{6378514^2 m^2} = 9.7964 \space m/s^2 g_{ust} = 6.674 \times 10^{-11} \frac{m^3}{kgs^2} \frac{5.972 \times 10^{24} kg}{6378928^2 m^2} = 9.79513 \space m/s^2

Gördüğünüz gibi yerçekimi ivmesi arasındaki fark çok küçük ama sıfır değil. İşte bu nedenle yüksek binalarda ağırlık merkezi kütle merkeziyle tam olarak aynı noktada olmaz.

Kütle Merkezi nedir?

Yerçekimi olsa da olmasa da cisimlerin kütlesi hep vardır. Kütle merkezi, cismin kütlesinin tamamının toplandığı kabul edilen bir noktadır. Düzgün geometrik şekili homojen (türdeş: tüm bölgelerindeki kütle aynı şekilde dağılmış) cisimlerde kütle merkezi, cismin geometrik merkezindedir. Kütle merkezi skaler bir büyüklüğün merkezidir.

Kütle ve ağırlık merkezinin yeri (koordinatları) nasıl bulunur?

Bu bölümde artık ağırlık ve kütle merkezlerinin yerini eşit olarak ele alacağız. Neden peki? Yorumlarda cevabınızı bekliyorum.

Ağırlık merkezinin yeri deneysel olarak nasıl bulunur?

Önce basit olandan başlayalım. Elimizde bir çubuk ya da kurşun kalem olsun. Çubuğu bir boyutlu bir cisim olarak modelliyoruz (kalınlığını ve yüksekliğini ihmal ediyoruz sadece boyunu ele alıyoruz), ayrıca türdeş olduğunu farz ediyoruz. Bu çubuğun ağırlık merkezini nasıl buluruz? İki kolay yöntem kullanılabilir. Biri çubuğu bir iple ortasından tavana asmak. Diğeri çubuğun ortasına aşağıdan bir destek koymak. Aşağıdaki durumda ilk yolu görüyorsunuz. Dört parçadan oluşan homojen (türdeş) çubuğun ağırlık merkezi çubuğun uzunluğunun yarısının olduğu nokta yani tam ortası.

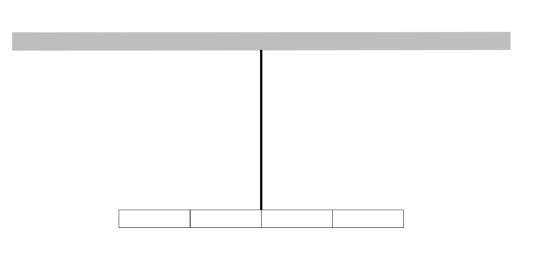
Bir tane de iki boyutlu cisme örnek verelim. Elimizde bir dikdörtgen levha olsun (bu kez de kalınlığı ihmal ettik). Bu levhanın ağırlık merkezini nasıl buluruz. Yine iple tavana asarız ama iki kez. Önce dikdörtgenin bir köşesinden sonra yanındaki diğer köşesinden. aşağıdaki resimde bu gösteriliyor.

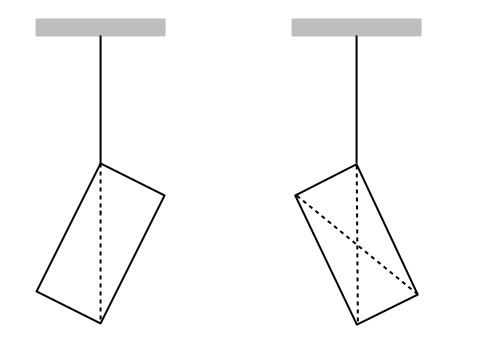
Dikkat edin, soldaki resimde ipin uzantısı dikdörtgenin köşegeninden geçiyor. Bunu işaretlersek sonra sağdaki gibi levhayı tekrar asarsak, bu kez ipin uzantısının dikdörtgenin diğer köşegeninden geçtiğini görüyoruz. Köşegenlerin kesiştiği nokta bu levhanın ağırlık merkezi.

Ağırlık merkezinin yeri fizik kanunlarıyla nasıl bulunur?

Fizik kanunları derken Newton’un hareket kanunlarından çıkarılan denge şartlarından bahsediyoruz. Hatırlayın, denge için iki şart vardı.

1. Net kuvvet sıfır olmalı.
2. Net tork sıfır olmalı.

Fikri anlamak için sadece üç parçacıktan oluşan bir cisim düşünelim. Sonra bunu n parçacığa genelleriz. Yine bir resimle görmeye çalışalım.

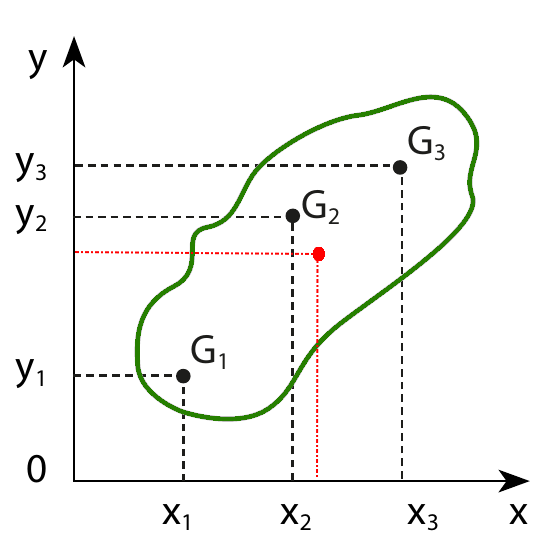
Yukarıdaki şekilde yeşil bölge bir cismi gösteriyor. Bu cisimde üç nokta seçtik, G₁, G₂ ve G₃. Kırmızı nokta henüz bilmediğimiz ama tahmin ettiğimiz ağırlık merkezi, koordinatlarına x_A, y_A diyelim.

Dengenin ilk şartı olarak toplam kuvvet sıfır. Yani bu cisim ivmelenmiyor, ağırlık merkezinden tutturulmuş ya da desteklenmiş. Biz asıl dengenin ikinci şartını kullanacağız. Öncelikle her noktadaki ağırlıkların toplamı cismin ağırlığına eşit (bunun vektörel toplam olduğuna dikkat edin).
m_1\vec{g} + m_2\vec{g} + m_3\vec{g} = m_{cisim}\vec{g}

Şimdi net torkun sıfır olması şartını yazalım:
\vec{\tau_1} + \vec{\tau_2} + \vec{\tau_3} = \vec{\tau_{cisim}}

Torku x ve y eksenlerinde ayrı ayrı incelersek, x ekseni için:
m_1gx_1 + m_1gx_2 + m_1gx_3 = m_{cisim}gx

Buradan:
x = \frac{m_1x_1 + m_2x_2 + m_3x_3}{m_1+m_2+m_3}

y ekseni için:
m_1gy_1 + m_1gy_2 + m_1gy_3 = m_{cisim}gy

Buradan da:

y = \frac{m_1y_1 + m_2y_2 + m_3y_3}{m_1+m_2+m_3}

Böylece ağırlık ve kütle merkezinin (x,y) koordinatlarını bulmuş oluruz.

Düzgün geometrik cisimlerin kütle merkezleri

Şekil	Kütle merkezinin yeri
Düz çubuk	Çubuğun tam orta noktası
Kare	Köşegenlerin kesişim noktası
Dikdörtgen	Köşegenlerin kesişim noktası
Üçgen	Kenarortayların kesişim noktası
Çember	Merkez noktası
Dairesel levha	Merkez noktası

Kütle merkezi ile ağırlık merkezi arasındaki fark nedir?

Toparlamak için bu soruyu sorduk, yanıtlayalım.

1. Kütle merkezi kütleyle ilgilidir, kuvvet ile ilgili değildir, yerçekimi ivmesiyle ilgili değildir. Cismin kütlesinin toplandığı varsayılan bir noktadır.
2. Ağırlık merkezi kuvvetle ilgilidir, yerçekimi ivmesiyle ilgilidir. Cismi oluşturan parçacıkların ağırlıklarının bileşkesinin uygulandığı noktadır.
3. Yer çekimi ivmesi sabitse (yerden yüksekliği pek değişmiyorsa) ağırlık merkezi ile kütle merkezi aynı noktada kabul edilir.
4. Yer çekimi ivmesi değişiyorsa (cismin altı ile üstü arasında önemli bir uzaklık farkı varsa) ağırlık merkezi ile kütle merkezi aynı noktada olmaz.

Öğrendiklerinizi pekiştirmek için şimdi sıra kütle ve ağırlık merkezi ile ilgili örnek soru çözümlerinde.

Bir yüzey üzerinde duran cisimlerin denge durumu

Aşağıdaki şekilde üç düzgün geometrik şekilli cisim gösteriliyor. Bu cisimlerin bir yüzey üzerinde durduklarını görüyoruz. Bu cisimlerin hangilerinin dengede duracağını hangisinin devrileceğini inceleyeceğiz.

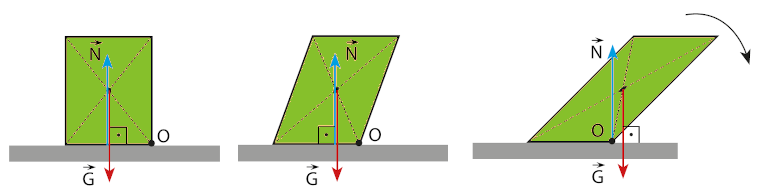
Eğer bir cisim yatay bir düzleme yerleştirildiyse bu cismin ağırlığı bulunduğu yüzeye her zaman diktir. Cismin ağırlığının doğrultusu cismin tabanın sınırları arasında kalırsa cisim bulunduğu zemin üzerinde dengede kalır. Soldaki ilk iki durumda cismin ağırlığı (G) ile zeminin tepki kuvetinin (N), O noktasına göre torkları birbirine eşit ve zıt yönlü olduğu için cisim dengededir. Ama en sağdaki durum farklı. Bu durumda cismin ağırlığının doğrultusu, cismin taban sınırları arasında değil bu nedenle cismin ağırlığının ve zeminin tepki kuvvetinin torkları birbirine eşit olamaz. Bu yüzden bu cisim dengede kalamaz ve devrilir.

Kütle ve Ağırlık merkezi ile ilgili kazanımlar

11.1.9.2. Kütle merkezi ve ağırlık merkezi kavramlarını açıklar.

• Kütle ve ağırlık merkezi kavramlarının farklı olduğu durumlara değinilir.