Çarklar ve Dişliler nedir? Örnek soru çözümleri

Çarklar ve dişliler sadece basit makinelerde değil, neredeyse tüm makinelerde en sık kullanılan sistem elemanlarıdır. Merkezi etrafında dönebilen, çevresine dişlerin sıralandığı çarklara dişli adı verilir. Bu çarklar çember, disk ya da silindir şeklinde olabilir. Dişlilerin kullanım amacı birlikte ve aynı anda çalışması gereken mekanik sistem elemanları arasındaki bağlantıyı sağlamaktır. Dişleri dişli çarklarda birbiri arasına girer, böylece bir dişli döndüğünde diğeri de döner. Bir çarkın üzerindeki diş sayısı çarkın yarıçapıyla doğru orantılıdır. Çarkın yarıçapı büyüdükçe diş sayısı da artar. Dişli çarklarda dönme yönü ve tur sayısı değiştirilerek istenilen biçimde iş yapma kolaylığı sağlanır. Günlük yaşamda dişli çarklar neredeyse tüm motorların, arabalarda vites kutusunun ve saatlerin yapımında kullanılır.

Yukarıdaki resimde bir bir makinede kullanılan dişli çark sistemi gösteriliyor. Şimdi çarkların farklı şekillerde nasıl kullanıldığını inceleyelim.

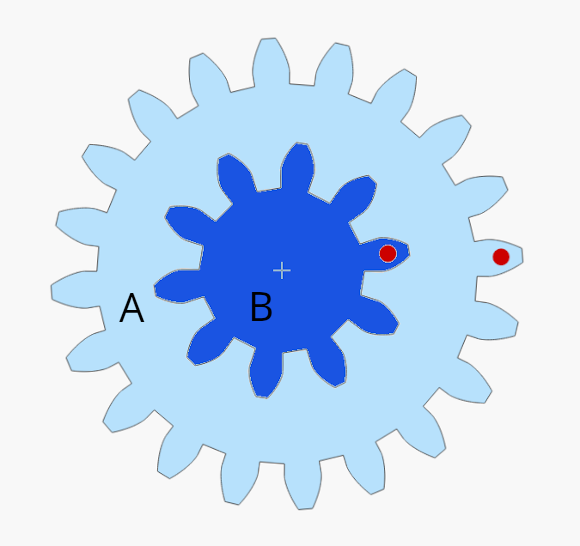
Yukarıdaki şekilde gösterilen A ve B dişlileri merkezleri aynı olacak biçimde (yani aynı eksende) birleştirilmiş. Bu sistemde A ve B dişlilerinin dönme yönü ve tur sayıları aynıdır, tıpkı çıkrık gibi. Dolayısıyla bu sistemde tur sayısı çarkların yarıçaplarından bağımsız. A çarkı bir kez döndüğünde B çarkı da bir kez dönüyor.

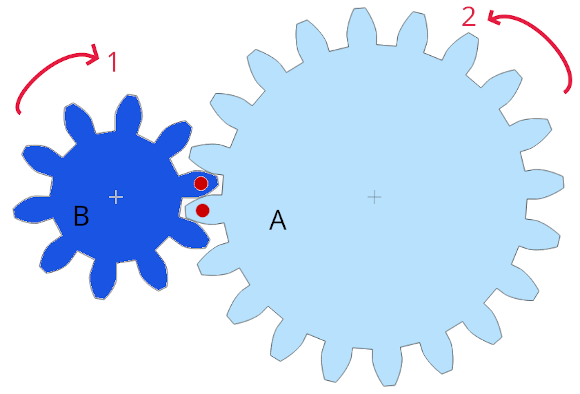
Bu kez yine yarıçapları farklı A ve B dişlilerini birbirine dıştan temas edecek şekilde birleştirelim. Bu sistemde A dişlisi 2 yönünde dönerse B dişlisini 1 yönünde dönmeye zorlar. A dişlisinin dönmesini sağlayan kuvvet B dişlisinin de dönmesine sebep olur. Yani F_A = F_B = F olur. Enerjinin korunumu ilkesine göre iki dişli üzerinde yapılan işler birbirine eşittir. A dişlisinin n_A tur döndüğünde B dişlisinin n_B tur döndüğü durumu ele alalım. Bu durumda:
F(2\pi r_A)n_A = F (2\pi r_B)n_B

n_A r_A = n_B r_B \frac{n_A}{n_B} = \frac{r_B}{r_A}

Bu sonucu yorumlayalım: A ve B dişlilerinin tur sayıları yarıçaplarının büyüklüğü ile ters orantılı, dişliler zıt yönde dönüyor.

Son olarak da A ve B dişlilerinin bir zincirle birbirine bağlandığı durumu inceleyelim. Bu durumda iki dişli de aynı yönde döner. Zincirin üzerindeki her noktada gerilme kuvveti aynıdır (zincirin esnemediğini ve sıkışmadığını kabul ediyoruz). Bu durumda enerjinin korunumuna göre A dişlisi ve B dişlisi üzerinde yapılan işler birbirine eşit olmalıdır. Öyleyse:
F(2\pi r_A)n_A = F(2\pi r_B)n_B

n_A r_A = n_B r_B \frac{n_A}{n_B} = \frac{r_B}{r_A}

Bu sonucu da yorumlayalım: A ve B dişlilerinin tur sayıları yarıçaplarının büyüklüğü ile ters orantılı, dişliler aynı yönde dönüyor.

Örnek soru 1

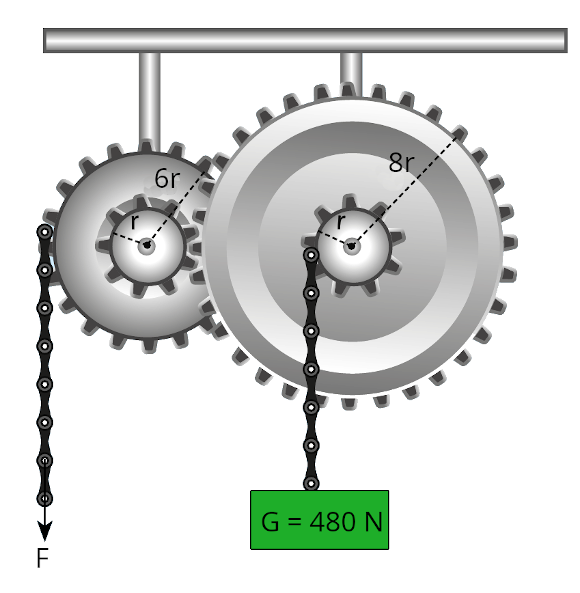
Şekilde gösterilen çark sisteminde yarıçapları r, 6r ve 8r olan dişliler birbirine bağlanmıştır. Bu sistemde ağırlığı 480 N olan cisim F kuvveti ile dengeleniyor. Buna göre F kuvvetinin büyüklüğü kaç Newtondur?

Çözüm

Fizikte genellikle yaptığımız ilk iş soruyu anlamak için şekil verildiyse tekrar çizmek. Öyle yapalım:

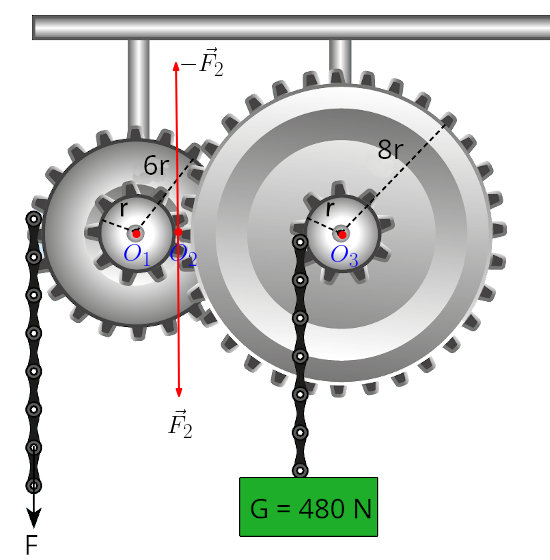
Bu sistemde üç önemli nokta belirledik: O₁ soldaki içiçe geçmiş dişlilerin merkezi , O₂ soldaki iç dişliyle sağdaki dış dişlinin temas noktası ve O₃ sağdaki içiçe geçmiş dişlilerin merkezi.

Sistemin dengede olduğunu biliyoruz, yani net tork sıfır. Önce soldaki çarkın tork formülünü yazalım. F₂ ile gösterilen O₂ noktasında soldaki iç dişlinin sağdaki dış dişliye uyguladığı kuvvet.
F \times 6r = F_2 \times r; \space F_2 = 6F

F₂ = 6F olduğunu bildiğimize göre, şimdi de sağdaki dişliler için tork denklemini yazabiliriz. Bu durumda etki tepki ilkesinden dolayı tepki kuvveti F₂‘nin zıt yönüne doğru, bu yüzden -F₂ olarak gösterdik.
F_2 \times 8r = 480 \times r

6F \times 8 = 480 \space N F = 10 \space N

Örnek soru 2

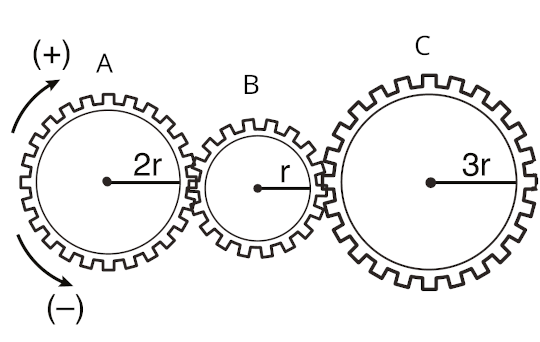
Yarıçapları sırasıyla 2r, r, 3r ve r olan A,B ve C dişlilerinden oluşan sistem şekilde gösterilmiştir. Buna göre A dişlisi (+) yönünde 6 devir yaptığında C dişlisi hangi yönde kaç devir (tur) yapar?

Çözüm

Önce yönü bulalım. A dişlisi (+) yönde dönerse B dişlisini zıt yönde yani (-) yönde dönmeye zorlar. B dişlisi (-) yönde döndüğüne göre de C dişlisini (+) yönde dönmeye zorlar. Yönü bulduk, şimdi turu hesaplayalım.

A dişlisi 6 tur dönerse B dişlisi:
n_A r_A = n_B r_B

6(2r) = n_B(r); \space n_B = 12

B dişlisi 12 tur dönerse C dişlisi:
n_B r_B = n_C r_C

12(r) = n_C (3r); \space n_C = \frac{12}{3} = 4

Demek ki C dişlisi 4 tur dönüyor.

Çarklar ve Dişliler ile ilgili Kazanımlar

11.1.10.1. Günlük hayatta kullanılan basit makinelerin işlevlerini açıklar.

• Kaldıraç, sabit ve hareketli makara, palanga, eğik düzlem, vida, çıkrık, çark ve kasnak ile sınırlı kalınır.

11.1.10.2. Basit makineler ile ilgili hesaplamalar yapar.

• İkiden fazla basit makinenin bir arada olduğu sistemlerle ilgili matematiksel hesaplamalara girilmez.
• Hesaplamaların günlük hayatta kullanılan basit makine örnekleri (anahtar gibi) üzerinden yapılması sağlanır.
• Basit makinelerde verim ile ilgili matematiksel hesaplamalar yapılması sağlanır.