Atwood makinesi nedir? Birbirine bağlı cisimler veya bloklar

Newton’un hareket yasalarının uygulanarak hareketlerinin açıklanmasına dinamik dendiğini bir önceki yazımızda açıklamıştık. Bu yazıda dinamik uygulamalarına birden fazla cisimden oluşan sistemlerin hareketini inceleyerek devam edeceğiz. Birbirine ip ya da çeki demiri gibi bağlantı elemanlarıyla bağlı cisimlerin hareketinin sebeplerini yani dinamiğini analiz edeceğiz. Sonra da Atwood makinesi neymiş öğreneceğiz.

Bir önceki yazıda tek cismin hareketini incelemiştik. Gerçek yaşamda çoğu zaman tek cisimlerle değil birden fazla cisimden oluşan sistemlerle karşılaşırız. Örneğin, bozulmuş bir arabayı bazen bir başka arabaya çekme halatıyla bağlayıp bir yerden bir yere götürmek gerekir. Boğazlarda römorkörler büyük gemileri halatlarla çekerler. Traktörler de arkalarına bağlanan römorkleri çeker. Bunun gibi durumları basitleştirerek şöyle modelleyebiliriz:

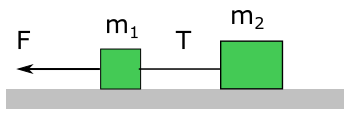
Bu resim hafif bir iple birbirine bağlandıktan sonra, sabit bir F kuvveti uygulanan iki cismi gösteriyor. En basit durumu ele alalım, sürtünmeyi de ihmal edelim. Bu cisimler nasıl hareket eder? İvmeleri ne olur? Bu sorulara yanıt vermek için dinamikte hep yaptığımız gibi serbest cisim diyagramlarını çizeceğiz.

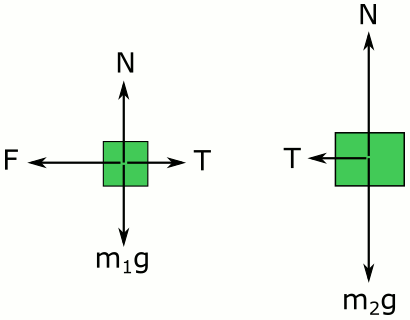
m₁ kütleli cisme düşeyde uygulanan kuvvetlerin toplamı sıfır olmak zorunda. Çünkü bu cisim düşeyde hareket etmiyor, Newton’un birinci kanunu eylemsizlik, dengelenmiş kuvvetlerin etkisindeki cisimlerin hareket durumlarının değişmeyeceğini söylüyor. Öyleyse

\vec{N} + (-m_1\vec{g}) = 0

Eksi işareti ağırlığın -y yönünde yani aşağı doğru olduğunu gösteriyor. Bu durumda:

\vec{N} = m_1\vec{g}

Yatayda ise sürtünme kuvveti olmadığı için, – x yönünde \vec{F} ve ip gerilmesi \vec{T} var ve birbirlerine zıt yöndeler. Bu cisim hareket ediyor, bu nedenle |F| > |T|. Newton’un ikinci hareket yasasını yazarsak:

\vec{F}_{1net} = m_1\vec{a} \vec{F}_{1net} = \vec{F} - \vec{T} \vec{F} - \vec{T} = m_1\vec{a} \space (1. denklem)

Şimdi de ikinci cisim için yatay doğrultuda Newton’un ikinci kanununun denklemini yazalım:

\vec{F}_{2net} = m_2\vec{a} \vec{F}_{2net} = \vec{T}

Net kuvvet sadece ip gerilmesine eşit çünkü yatayda bu cismin üzerine etkiyen başka kuvvet yok. Ayrıca ivmeler de birbirine eşit olmak zorunda çünkü her iki cisim de birlikte hareket ediyor. Öyleyse:

\vec{T} = m_2\vec{a} \space (2. denklem)

İp aynı ip, gerilmesi de her noktasında aynı, dolayısıyla T her iki cisim için de aynı büyüklükte olmalı. İkinci denklemdeki eşitliği birinci denklemde yerine koyalım. burada F, m₁ kütleli cismi çeken kuvvet.

\vec{F} - m_2\vec{a} = m_1\vec{a} \vec{F} = m_1\vec{a} + m_2\vec{a} \vec{F} = (m_1 + m_2)\vec{a}

Vardığımız sonuç şu: birbirine iple bağlı iki cismi, kütlelerini toplayıp tek bir cisim olarak gibi değerlendirebiliriz.

Örnek soru 1:

Sürtünmesiz bir yüzeyde, kütleleri sırasıyla m₁ = 2 kg ve m₂ = 6 kg olan iki cisim birbirine kütlesi önemsenmeyen bir halatla bağlanmıştır. m₁ cismi 36 N kuvvetle yatay doğrultuda çekiliyor. Buna göre: (g = 10 m/s²)

(a) Sistemin ivmesinin büyüklüğü kaç m/s²‘dir?

(b) İp gerilmesi kaç N olur?

(c) Aynı kuvvet yalnızca m₂ kütleli cisme uygulanırsa ip gerilmesi kaç N olur?

Çözüm:

(a) Bu soru yukarıdaki incelememizin sayı verilmiş halinden başka birşey değil. Tek yapmamız gereken önce durumun şeklini sonra cisimlerin serbest cisim diyagramını çizmek, ardından adım adım analizi uygulamak.

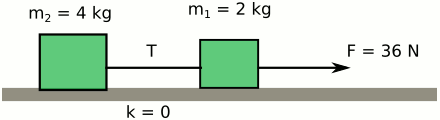
Yukarıdaki resimde soruda bize verilen durumu çizdik. Şimdi cisimlerin serbest cisim diyagramlarını çizelim.

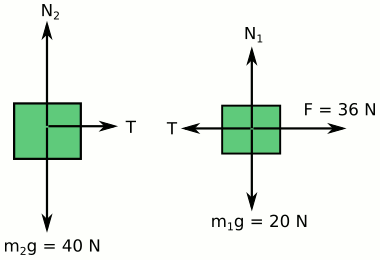
Her iki cisim için de düşeyde hareket durumunun değişmesi söz konusu değil, bu nedenle:

\vec{N}_1 - m_1\vec{g} = 0 \vec{N}_2 - m_2\vec{g} = 0

Sadece yatayda net kuvvet var. Yukarıdaki analizimizden bu iki cismin tek bir cisim gibi davrandığını biliyoruz. Öyleyse:

\vec{F} = (m_1 + m_2)\vec{a} 36 \space N = (2 + 4)\vec{a} \vec{a} = \frac{36 \space N}{6 \space kg} = 6 \space m/s^2

İvmenin büyüklüğünü 6 m/s² olarak bulduk.

(b) İp gerilmesini birinci ya da ikinci cismin serbest cisim diyagramını kullanarak bulabiliriz. İkinci cisminki daha kolay.

\vec{F}_{2net} = m_2\vec{a} \vec{F}_{2net} = \vec{T} \vec{T} = m_2\vec{a} \vec{T} = 4 \space kg \times 6 \space m/s^2 = 24 \space N

(c) Şimdi kuvvetin uygulandığı noktayı değiştiriyoruz. Tekrar resim ve serbest cisim diyagramı çizelim.

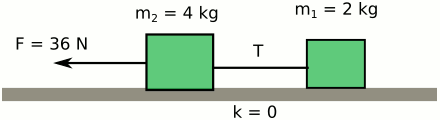
Pek bir şey değişmemiş gibi gelebilir size, gerçekten de ivme değişmez. Ama serbest cisim diyagramını çizmeliyiz ki ip gerilmesini görebilelim.

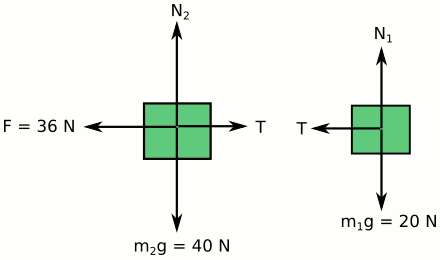
İvme değişmeyecek çünkü iki cisimden oluşan bu sistem hala tek cisimmiş gibi hareket ediyor. Ama ip gerilmesi değişecek. Birinci cismin serbest cisim diyagramını kullanarak hesaplayalım.

\vec{F}_{1net} = m_1\vec{a} \vec{F}_{1net} = \vec{T} \vec{T} = m_1\vec{a} \vec{T} = 2 \space kg \times 6 \space m/s^2 = 12 \space N

İp gerilmesi ilk duruma göre yarıya indi.

Örnek soru 2: Uyarlanmış Atwood makinesi

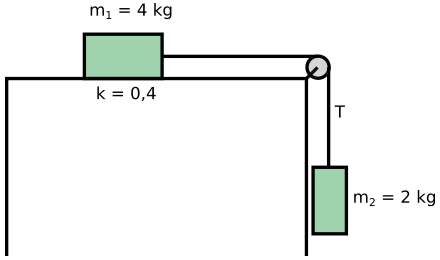
Şekilde bir öğrencinin kurduğu deney düzeneği gösterilmiştir. Öğrenci yatay bir masanın üstüne 4 kg kütleli bir tahta takozu koymuş, bunu 2 kg kütleli bir başka takoza hafif bir iple bağlamış, bir makara kullanarak ikinci cismi düşey de serbest bırakmıştır. Masayla takoz arasındaki sürtünme katsayısı k = 0,4 olduğuna göre ip gerilmesi kaç N olur? (g = 10 m/s²)

Çözüm:

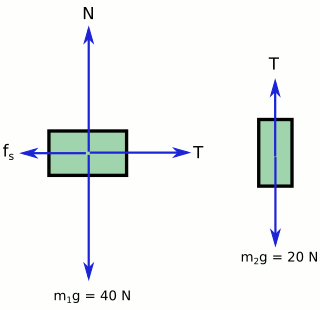
Daha önce böyle bir durumla karşılaşmamış olabiliriz. Cismin biri yatayda diğeri düşeyde hareket ediyor. Korkmaya gerek yok, yine serbest cisim diyagramlarını çizip durumu inceleyeceğiz. (Bu aslında uyarlanmış bir Atwood makinesi, aşağıda Atwood makinesini göreceksiniz.)

Birinci cisim düşeyde (y doğrultusunda) hareket etmiyor. Öyleyse:

\vec{N} = m_1\vec{g} \vec{N} = 40 \space N

Şİmdi de yataydaki kuvvetlere bakalım. Newton’un ikinci kanunu yazalım:

\vec{T} - \vec{f}_s = m_1\vec{a} \vec{f}_s = k\vec{N} \vec{f}_s = 0,4 \times 40 \space N = 16 \space N \vec{T} -16 \space N = 4\vec{a} \space (1. denklem)

Şimdi de ikinci cisim için Newton’un ikinci hareket kanununu yazalım. İkinci cismin üzerinde yukarı doğru T aşağı doğru ağırlığından başka kuvvet yok.

m_2\vec{g} - \vec{T} = m_2\vec{a}

Buradan T’yi çekebiliriz:

\vec{T} = m_2\vec{g} -m_2\vec{a} \vec{T} = 20 \space N -2\vec{a}

Şimdi T’yi 1. denklemde yerine koyalım.

20 \space N -2\vec{a} - 16 \space N = 4\vec{a} 6\vec{a} = 4 \space N \vec{a} = \frac{4 \space N}{6 \space kg} = \frac{2}{3}m/s^2

İvmeyi bulduk artık ip gerilmesini de bulabiliriz:

\vec{T} = 20 \space N -2\vec{a} \vec{T} = 20 \space N -2 \frac{2}{3}kg m/s^2 \vec{T} = \frac{60-8}{3} = \frac{52}{3} = 17,3 \space N

Dikkat etmeniz gereken rakamlar değil, serbest cisim diyagramlarından yazdığınız kuvvet ve ivme ilişkileri.

Örnek soru 3:

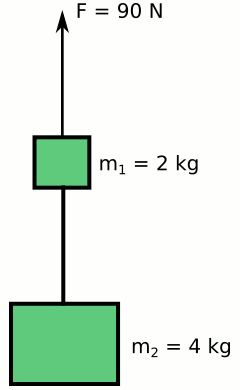
Şekilde kütleleri sırasıyla 2 kg ve 4 kg olan iki cisim birbirine hafif bir iple bağlanmıştır. Üstteki 2 kg’lık cisim 90 N’luk kuvvetle +y yönünde çekildiğine göre ip gerilmesi kaç N olur? (Hava sürtünmesi önemsenmeyecektir, g = 10 m/s²).

Çözüm:

Bu kez yatayda hareket yok sadece düşeyde hareket var. Yine serbest cisim diyagramlarını çizip Newton’un ikinci kanunu yazıp çözeceğiz. Önce ilk cismi çizelim:

\vec{F} - (m_1\vec{g} + \vec{T}) = m_1\vec{a} 90-20-\vec{T} = 2\vec{a} \vec{T} = 70 - 2\vec{a} (1.denklem)

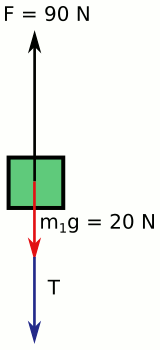
Şimdi ikinci cismi çizelim:

\vec{T} - m_2\vec{g} = m_2\vec{a} \vec{T} = 40 + 4\vec{a}

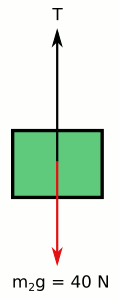
Bunu 1. denklemde yerine koyalım:

70 - 2\vec{a}=40 + 4\vec{a} 6\vec{a} = 70 - 40 \space N \vec{a} = \frac{30 \space N}{6 \space kg} = 5 \space m/s^2

İvmeyi bulduk, yönü +y, yukarı doğru (işareti artı). Şimdi ip gerilmesini bulabiliriz.

\vec{T} = 40 + 4\vec{a} \vec{T} = 40 + 4.5 = 40 + 20 = 60 \space N

Atwood makinesi veya düzeneği nedir?

Atwood makinesi dinamiğin temel ilkelerini göstermekte kullanılan bir fizik deneyi düzeneğidir. 1784 yılında İngiliz matematikçi George Atwood tarafından hareket yasalarının mekaniğini (naıl işlediğini) göstermek için icad edilmiştir. Genellikle bir makara, bir ip ve iki kütleden oluşşan bir sistemdir. Sabit ivme elde edebilmeyi sağlar. Atwood makinesi problemlerini çözerken dikkat etmeniz gereken ipin ya da halatın aktardığı gerilme kuvvetinin tüm ip boyunca aynı olduğunu fark etmektir.

Aşağıdaki şekilde ideal bir Atwood makinesi gösteriliyor. Makaranın ve ipin kütleleri önemsenmiyor ve sürtünme de ihmal ediliyor. m₁ > m₂ olduğunu da biliyoruz.

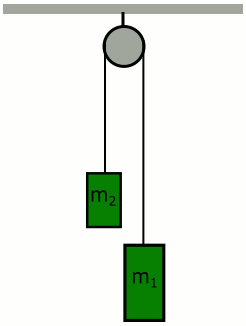
Bu sistemin ivmesini ve ip gerilmesini nasıl buluruz? Önce serbest cisim diyagramını çizelim sonra Newton’un ikinci kanunu yazalım:

\vec{F}_{1net} = m_1\vec{a} \vec{F}_{1net }=m_1\vec{g} - \vec{T} = m_1\vec{a} \vec{T} = m_1(\vec{g}-\vec{a}) \vec{F}_{2net} = m_2\vec{a} \vec{F}_{2net }= \vec{T} - m_2\vec{g} = m_2\vec{a} \vec{T} = m_2(\vec{g}+\vec{a})

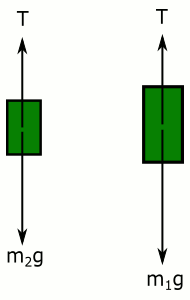
T ve a (ip gerilmesi ve ivmenin büyüklükleri) iki cisim için de aynı olmak zorunda. Çünkü ip gerilmesi ipin her noktasında aynı büyüklükte ve cisimler ipe bağlı oldukları için birlikte hareket ediyorlar. İp gerilmelerini birbirine eşitleyebiliriz:

\vec{T} = m_1(\vec{g}-\vec{a})=m_2(\vec{g}+\vec{a})

Buradan ivmeyi bulabiliriz. (Sadece vektörlerin büyüklüklerini yazalım:)

m_1g -m_1a = m_2g + m_2a m_1g - m_2g = m_1a + m_2a (m_1-m_2)g = (m_1+m_2)a a = g(\frac{m_1-m_2}{m_1+m_2})

Örnek soru 4:

Şekildeki sürtünmelerin önemsenmediği makaranın ve ipin kütlelerinin ihmal edildiği Atwood makinesi düzeneğinde m₁ = 4 kg ve m₂ = 1 kg ise, sistemin ivmesi kaç m/s² ve ipteki gerilme kuvveti kaç N olur? (g = 10 m/s²⁾

Çözüm:

Bu soru yukarıdaki analizimizin sadece rakam verilmiş hali. Yapmanız gereken yine serbest cisim diyagramlarını çizip, Newton’un ikinci kanunu her cisim için yazmak, sonra da ip gerilmelerini birbirine eşitlemek. Serbest cisim diyagramını siz çizin.

\vec{F}_{1net }=m_1\vec{g} - \vec{T} = m_1\vec{a} \vec{T} = m_1(\vec{g}-\vec{a}) \vec{F}_{2net }= \vec{T} - m_2\vec{g} = m_2\vec{a} \vec{T} = m_2(\vec{g}+\vec{a}) \vec{T} = m_1(\vec{g}-\vec{a})=m_2(\vec{g}+\vec{a}) 40 - 4a = 10 + a 5a = 40 - 10 = 30 a = \frac{30 \space N}{5 \space kg} = 6 \space m/s^2

İvmeyi bulduk, ip gerilmesi için yerine yerleştirelim.

\vec{T} = m_1(\vec{g}-\vec{a}) T=4(10-6) = 4.4 = 16 \space N

Aşağıdaki video bir laboratuvarda kurulmuş bir Atwood makinesi gösteriliyor.

Dinamik ile ilgili mutlaka okumanız gereken yazılar

1. Dinamik nedir? Sürtünmesiz düzlemde sorular ve çözümler
2. Dinamik soruları ve çözümleri
3. Eğik düzlem nedir? Sorular ve çözümler
4. Eylemsizlik kuvveti nedir? Asansör soruları

Atwood makinesi ve birbirine bağlı cisimler ile ilgili kazanımlar

2017 – 11.1.3.1. Net kuvvetin yönünü belirleyerek büyüklüğünü hesaplar.

• Serbest cisim diyagramları üzerinde cisme etki eden kuvvetlerin gösterilmesi sağlanır.
• Yatay, düşey ve eğik düzlemde sürtünme kuvvetinin yönü belirlenerek büyüklüğünün hesaplanması sağlanır.

2017 – 11.1.3.2. Net kuvvet etkisindeki cismin hareketi ile ilgili hesaplamalar yapar.

• Hesaplamaların günlük hayat örnekleri üzerinden yapılmasına özen gösterilir.
• Sürtünmeli ve sürtünmesiz yüzeyler dikkate alınmalıdır.