Dönerek Öteleme Hareketi Nedir?

Daha önce hareket çeşitlerini öğrendiğinizde öteleme hareketinin bir cismin düz bir yol (bu yola yörünge denir) boyunca, belirli bir doğrultuda ve yönde ilerlemesi olduğunu öğrenmiştiniz. Dönme hareketinin de bir cismin belli bir nokta (bu noktaya eksen denir) etrafında dönmesi olduğunu görmüştünüz. Dönme hareketi yapan bir cismin ekseni etrafındaki tüm noktalar çembersel hareket yapar; ancak dönme ekseni üzerinde kalan noktalar olduğu yerde döner. Dönerek öteleme hareketi bu iki hareket çeşidinin aynı anda olmasıdır. Bu hareket türünün en güzel örneği de bir tekerleğin kaymadan dönme ve öteleme hareketini birlikte yaparak ilerlemesidir. Şimdi bir bisiklet tekerini bir çember olarak modelleyip bu hareket neye benziyor aşağıdaki animasyonda inceleyelim.

Tekerleğin üzerinde seçtiğimiz kırmızı noktanın hareketine dikkatli bakın. Hangi tür hareketi yapıyor? Dönme değil mi? Peki tekerleğin ağırlık merkezi hangi tür hareketi yapıyor? Ağırlık merkezi çemberin de merkezi, küçük siyah nokta. Öteleme hareketi yapıyor. Ayrıca tekerleğin kaymadığına da dikkat edin. Kırmızı noktanın kırmızı eğri ile gösterilen yörüngesinin özel bir adı var: sikloid (parabol ya da doğru gibi).

Şimdi de dönerek öteleme hareketinde hızı inceleyelim. Hızın vektörel bir büyüklük olduğunu hatırlatalım. Aşağıdaki animasyonda az önceki tekerleğin bu kez hız vektörleri gösteriliyor.

Kırmızı noktaya odaklanın. Bu noktanın yatay bir hızı olduğuna (x eksenine paralel) dikkat edin. Bu yatay hız vektörünün yönü hiç değişmiyor. Bir de kırmızı noktanın çembere teğet olan, dönme hareketinden kaynaklanan hızı var. Bu hız vektörünün yönü sürekli değişiyor. Yatay ve dikey hız vektörlerinin vektörel toplamı, yani bileşke hızın da hem büyüklüğü hem de yönü değişiyor. Peki yatay ve dikey hız bileşenlerinin büyüklüğünün aynı olduğunu farkedebildiniz mi? Açıklayalım.

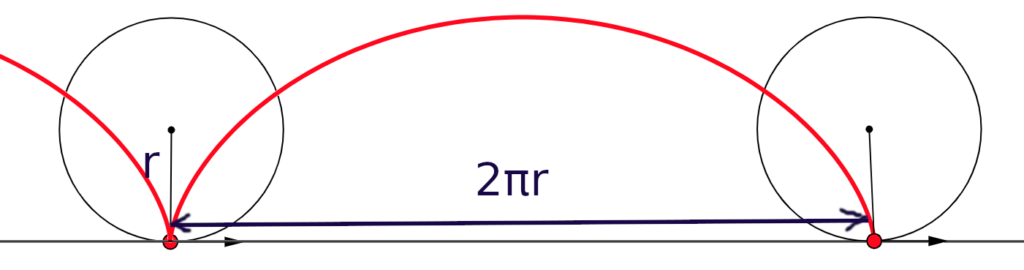
Yukarıdaki resimde kırmızı noktanın çemberin üstünde bir tam tur atıp tekrar başladığı yere dönmesi gösteriliyor. Bir tam tur demek çemberin çevresi demek yani aldığı yol 2πr. Bu yolun t saniye kadar sürdüğünü varsayarsak, dönme hızı v_dönme = 2πr/t olur. Tekerlek kaymadan sadece dönerek ilerlediği için t sürede çemberin merkezinin aldığı yol da çemberin çevresine eşit olur yani 2πr’ye. Öyleyse çemberin öteleme hızı da v_öteleme = 2πr/t olur.

Peki verilen bir noktanın yere göre anlık hızını nasıl hesaplarız? Bunu da gösterelim.

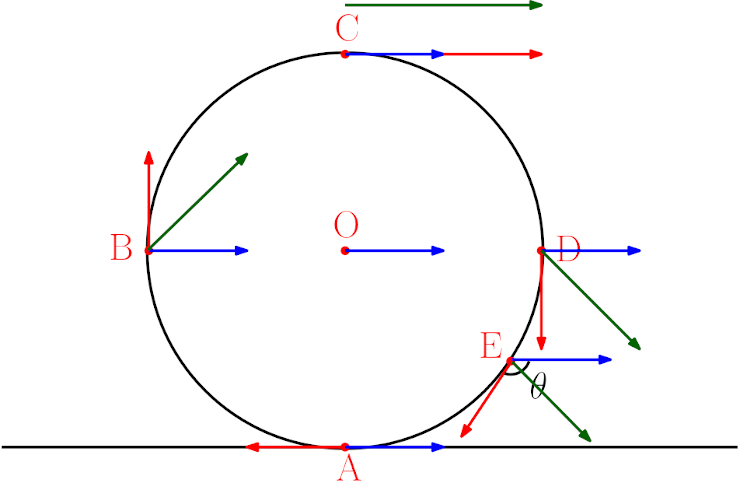
Yukarıdaki resim biraz karışık gibi gelebilir. Adım adım anlatalım. Dönerek ilerleyen çemberin üstündeki noktaları görüyoruz. Çemberin öteleme hızı v, mavi okla gösterilmiş. Çemberin merkezinin yere göre sadece öteleme hızı, çemberin üzerindeki diğer tüm noktaların ise yere göre hem öteleme hem de dönme hızları olduğuna dikkat edin. Çemberin üstündeki noktaların dönme hızlarının büyüklüğü de v, ama yönleri değişiyor, bu dönme hız vektörü de kırmızı okla gösterilmiş. Yeşil ok da bileşke hız vektörünü gösteriyor. Şimdi sırayla bakalım:

• A noktasında öteleme ve dönme hızları zıt yönlü, büyüklükleri de eşit. Vektörleri topladığımızda bileşkenin sıfır olduğunu görüyoruz. Yani tekerlek yere temas ettikleri anda yerden bakan bir gözlemciye göre duruyormuş gibi görünüyor. Bağıl hızı hatırlayın.
• B noktasında birbirine öteleme ve dönme hız vektörlerinin birbirine dik olduğunu görüyoruz. Vektör toplamı yaparsak bu noktadaki bileşke hızın büyüklüğü kaç v olur? v√2.
• C noktasında öteleme ve dönme vektörleri aynı yönlü, vektörleri topladığımızda bu noktadaki bileşke hızın 2v olduğunu görüyoruz.
• D noktası tıpkı B noktası gibi. v√2
• E noktası ise en genel hali: İki hız vektörünün bileşkesini kosinüs teoremine göre bulabiliriz:

v²_bileşke = v² + v² + 2vv(cosθ) = 2v² (1+cosθ)
v_bileşke = (v√2)√(1+cosθ)

Örnek soru

Bir araba 20 m/s süratle düzgün doğrusal hareket yapmaktadır. Arabanın tekerleklerinden birinin üzerindeki bir noktanın yatayla yaptığı açı 120° olduğuna göre, yerden bakan gözlemci bu noktanın hızını kaç m/s olarak görür?

Çözüm

Bu soru yukarıdaki şekildeki E noktasını tarif ediyor. İstersek vektörleri çizip bulabiliriz, istersek cosinus teoremini kullanabiliriz. Ben ikinci yoldan çözeyim:

v_{bileske} = v\sqrt{2}(\sqrt{1 + cos\theta}) v_{bileske} = 20\sqrt{2}(\sqrt{1+(-\frac{1}{2})}) = 20\sqrt{2}(\sqrt{\frac{1}{2}}) = 20 m/s

Dönerek öteleme hareketi ile ilgili kazanımlar

• 12.1.2.1. Öteleme ve dönme hareketini karşılaştırır.