Düzgün çembersel hareketi niye öğreniyoruz? Ne işimize yarayacak bu bilgi? Sınavda çıkacak bu kadar mı? Hiç bir şey de kullanmayacaksanız, araba kullanırken virajlara yavaş girmeniz gerektiği konusunda kullanacaksınız.
Bu yazıda yatay, düşey ve eğimli virajlarda emniyetli dönüş şartlarını inceleyeceğiz. Araba kullanırken viraja hızlı girerseniz ne olabilir (hatta neredeyse kesinlikle olur)? Aşağıdaki resimdeki gibi bir felaketle karşılaşabilirsiniz.

Bu resimdeki araba virajı alamadı, yoldan çıktı ve uçurumdan uçtu. Ama neden? Tabii ki viraja fazla hızlı girdiği için. Ama tam olarak ne kadar yavaş girmesi gerekirdi, sürati ne kadar olmalıydı ki devrilmesin?
Yatay düzlemdeki virajlarda emniyetli dönüş şartları
Yatay bir viraja giren arabayı, virajı bir çember olarak modelleyerek inceleyebiliriz. Aşağıdaki resimde bir arabanın böyle bir viraja girerken üstten görünüşü gösteriliyor.
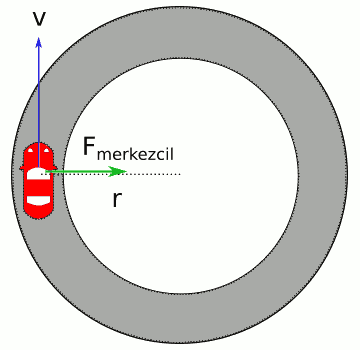
Arabanın çizgisel hızının yönünü değiştirip çembersel hareket yapmasını sağlayacak bir merkezcil kuvvete gereksinim var. Yoksa araba dümdüz gider (eylemsizliği hatırlayın), yukarıdaki uçurumdan uçan araba gibi virajı alamaz yoldan çıkar. Merkezcil kuvvetin kaynağı da arabanın tekerleri ile yol arasındaki sürtünme kuvveti. Öyleyse:
F{merkezcil} = F{surtunme} = m\frac{v^2}{r} = m\omega^2rBu eşitlik sağlandığı sürece araba çembersel hareket yapabilir, sürtünme kuvvetinin yeterince büyük olması lazım. Yani:
F{surtunme} \geq m\frac{v^2}{r}Öyleyse arabanın viraja emniyetli giriş şartı süratinin (hız vektörünün büyüklüğünün) şu değerin altında olmasıdır:
v^2 \leq \frac{F{surtunme} \times r}{m}Sürtünme kuvvetinin F{surtunme} = kmg olduğunu bildiğimize göre (arabanın yatay düzlemde olduğuna normal kuvvetin de ağırlığına eşit olduğuna dikkat edin):
v^2 \leq \frac{k\cancel{m}gr}{\cancel{m}}; \space v^2 \leq kgrBu süratten daha hızlı viraja girerse çembersel hareket yapamaz, savrulur, yoldan çıkar. Emniyetli dönüş hızının sürtünme katsayısıyla ve virajın yarıçapıyla doğru orantılı olduğuna dikkat edin. Buradan pratik iki sonuç çıkıyor:
- Yağışlı havalarda sürtünme katsayısı azaldığı için, kuru havalara göre virajlara daha yavaş girmek gerekir.
- Yarıçap azaldığı için dar virajlar, geniş virajlara göre daha tehlikelidir ve daha yavaş girilmelidir.
Düşey düzlemdeki virajlarda emniyetli dönüş şartları
Yatayı anladık da düşey düzlemde viraj mı olur? Gösterelim: Kaykaycıların döngü şeklindeki rampaları, eğlence parklarındaki hız trenlerinin (roller coaster) döngü şeklindeki rayları, bir arabanın tepeye ya da çukura girerken izlediği yol düşey virajlardır. Sırayla bakalım:

Yukarıdaki resimde bir kaykaycı çember şeklinde (aslında sarmal [spiral ya da heliks]) bir rampayı tamamlıyor. Eğer yeterince hızlı olmasaydı düşerdi. Peki rampaya girerken tam olarak süratinin (hızının büyüklüğünün) en az ne kadar olması lazım ki rampayı düşmeden tamamlayabilsin? Bu soruyu incelemek için Enerji Kaykay Parkı Simülasyonunu kullanacağız. Aşağıdaki resimde kaykaycının hareketi görülüyor.
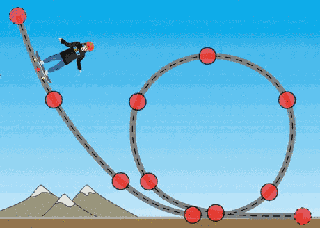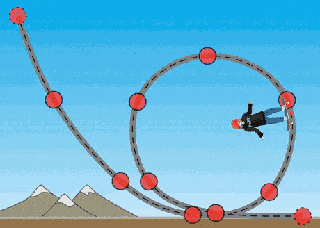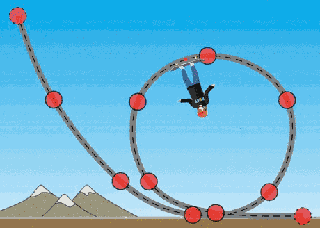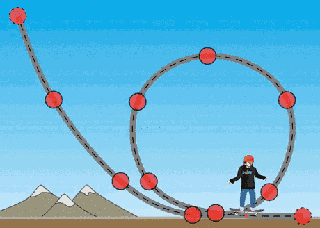
Kaykaycının hareketinin üç noktasını inceleyelim: (1) Döngünün en altı, (2) yere dik olduğu nokta ve (3) döngünün tepe noktası. Her biri için serbest cisim diyagramını çizeceğiz, kaykaycının üzerindeki kuvvetleri göstereceğiz.
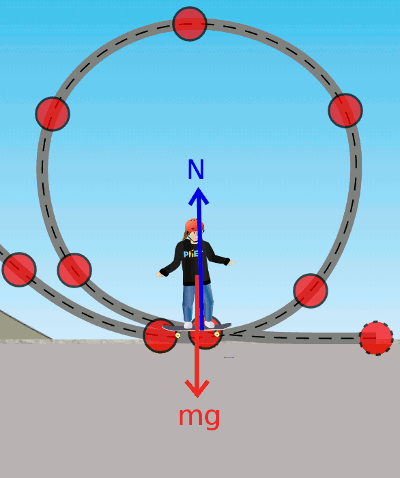
(1) Döngünün en altında kaykaycının üzerine etkiyen hem ağırlığı hem de tepki kuvveti var. Bu iki kuvvet zıt yönde, merkezcil kuvveti bulmak için vektörleri toplarız:
\vec{F}_{merkezcil} = \vec{N} + m\vec{g}Net kuvvetin büyüklüğü, zıt vektörler olduğu için normal kuvvetin büyüklüğünün ağırlığın büyüklüğünden çıkarılmasıyla bulunabilir:
F_{merkezcil} = N - mg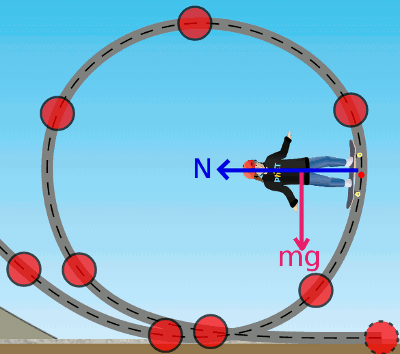
(2) Kaykaycının rampada yere dik olduğu noktada yine ağırlık kuvveti ve rampanın tepki kuvveti var. Ama birbirlerine dikler. Merkezcil kuvvet sadece kaykaycıyı çembersel yörüngenin merkezine doğru iten normal kuvveti. Öyleyse bu noktada:
\vec{F}_{merkezcil} = \vec{N}Merkezcil kuvvetin büyüklüğü de normal kuvvetin büyüklüğüne eşit. Fmerkezcil = N.
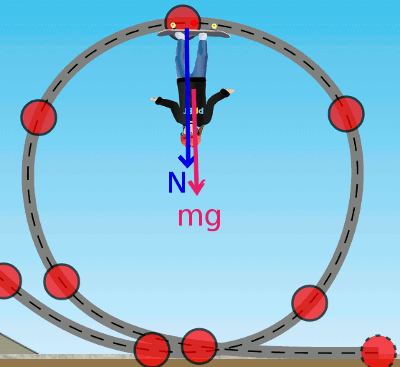
(3) Döngünün tepe noktasında kaykaycının üzerinde yine ağırlığı ve rampanın tepki kuvveti var. İkisi de aynı yönlü, öyleyse merkezcil kuvvetin büyüklüğü bu ikisinin büyüklüklerinin toplamına eşit.
Kaykaycının düşey çembersel yörüngenin tepe noktasından düşmeden güvenli bir şekilde geçebilmesi için:
F_{merkezcil}=m\frac{v^2}{r}eşitliğinin sağlanması gerekir. Normal kuvveti (rampanın tepki kuvveti) sıfır olduğu durumda: (N = 0)
mg = m\frac{v^2}{r}olmak zorundadır. Buradan kaykaycının güvenli bir şekilde düşey virajı tamamlayabileceği süratin en küçük değerini bulabiliriz:
v^2 = \frac{\cancel{m}gr}{\cancel{m}} = gr v = \sqrt {gr}Kaykaycının düşey düzlemin en üst noktasından geçebilmesi için sahip olması gereken en küçük sürat değeri, yer çekim ivmesine ve yörünge yarıçapının kareköküne bağlıdır.
Siz de aşağıdaki resimde rampasına Damien Walters’ın düşey sarmal rampaya giriş hızını bulabilir misiniz? Boyunu 1,80 m alabilirsiniz, buradan da çemberin yarıçapını kestirebilirsiniz.

Eğimli virajlarda hareket ve güvenli dönüş şartları
Dikkat ettiyseniz otoyollarda bazı virajları eğimli yaparlar. Neden acaba? Önce uç bir örneğe bakıp Pakistan’daki cehennem çukuru yarışı dedikleri motosiklet ve arabaların oldukça eğimli bir düzlemde nasıl döndüklerini görelim.

Bu araçlar nasıl oluyor da bu kadar dik bir eğimde düşmeden dönebiliyorlar? Yeterince hızlı olmasalar ne olur? Çok hızlı giderlerse ne olur? Bir kareyi durdurup eğimli virajdaki bir arabanın serbest cisim diyagramını çizelim.
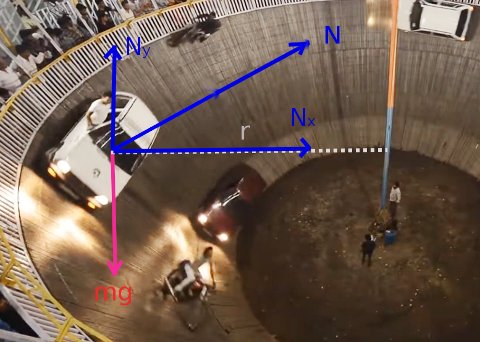
Arabanın ağırlığı (mg) yere doğru düşey doğrultuda. Rampanın uyguladığı tepki kuvvetini (N) de görüyoruz, rampaya dik doğrultuda. Sürtünme kuvvetini de ihmal edelim, işimiz kolay olsun diye. Tepki kuvvetini bileşenlerine ayıralım. Bu durumda arabanın ağırlığı Ny eşit olmalı ki arabanın ağırlığını dengelesin araba düşeyde hareket etmesin:
N_y = mgArabanın çembersel hareket yapmasının nedeni de merkezcil kuvvetin kaynağı olan tepki kuvvetinin x bileşeni. Öyleyse:
F_{merkezcil} = N_x = m\frac{v^2}{r}Rampanın (bu kesitin bir eğik düzlem olduğuna dikkat edin) eğimini bilirsek bu iki ilişkiyi birbirine bağlayabiliriz. Onun için bir serbest cisim diyagramı daha çizelim.
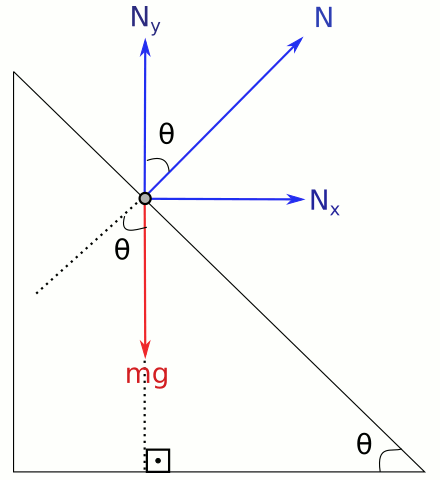
Bu şekil daha net görmemizi sağlıyor, arabayı bir nokta olarak gösterdik. Rampanın yatayla yaptığı θ açısını kullanarak, rampanın dik üçgen özelliğiyle N ile Ny arasındaki açının da θ olduğunu bulduk. (Bunu nasıl bulduğumuzu anlamanız önemli. Adım adım yapmaya çalışın.) Şimdi elimizde şu iki eşitlik var:
N_y = Ncos\theta = mgve
N_x = Nsin\theta= m\frac{v^2}{r}Her iki denklemde de N’leri yalnız bırakırsak:
N = \frac{mg}{cos\theta} N = m\frac{v^2}{rsin\theta}Birbirine artık eşitleyebiliriz çünkü N = N.
\frac{mg}{cos\theta} = m\frac{v^2}{rsin\theta}v’yi bulmak istiyoruz, v’yi yalnız bırakalım:
v^2 = \frac{\cancel{m}grsin\theta}{\cancel{m}cos\theta} tan\theta = \frac{sin\theta}{cos\theta}olduğunu biliyoruz. Öyleyse:
v=\sqrt{grtan\theta}Bir aracın eğimli bir virajı güvenli bir şekilde dönebilmesi için gerekli süratinin yarıçapın ve eğimin (tanθ’ya eğim adı da verilir) kareköküyle doğru orantılı olduğunu bulduk.
Yatay, düşey, eğimli virajlar ile ilgili Kazanımlar
12.1.1.4. Yatay, düşey, eğimli zeminlerde araçların emniyetli dönüş şartları ile ilgili hesaplamalar yapar.
- Virajlarda emniyetli dönüş için hız sınırına uymanın önemi vurgulanır.
Yatay, düşey, eğimli virajlar ile ilgili MEB ve EBA Testleri
- Düzgün Çembersel Hareket 2 – Test – 2 (2016- 2017)
- Düzgün Çembersel Hareket 3 – Test – 3 (2017- 2018)
- Cevap anahtarlarına buradan bakabilirsiniz:
Viraja giriş yapmak için güvenli hızı yazarken yanlış yapmışsın tekrar bak
V küçükeşittir k.g.r demişsin
Doğrusu
V küçükeşittir kök( k.g.r) veya
V kare küçükeşittir k.g.r
Teşekkürler hoşçakal
Dikkatin harika. Düzeltildi.
Ny=Ncosθ=mg
Fakat mgcosθ=N de yazabiliriz
Nasıl Ncosθ mg ye mgcosθ ise N ye eşit olabilir ki ?
Eğik düzlemle ilgili yazdığınız yazıda mgcosθ=N yazmıştınız
mgsinθ = N, cosθ değil. Serbest cisim diyaramını dikkatli inceleyin, θ açısı nerede.
Mukemmel anlatim icin sag olun. Basit Harmonik Hareket ne zaman gelecek?
Yakın bir zamanda.
Gelmedi 🙁
Hâlâ gelmemiş olması üzdü…
harmonik nerdeee
Fm sürtünme kuvvetine eşitse nasıl fm büyük olabilir yada fsürtünme fm den büyük olmalıdır diyebiliriz ki
Fmerkezcil = Fsürtünme bu merkezcil kuvvetin kaynağının sürtünme kuvveti olduğunu söylüyor. Dönüşün emniyetli olabilmesi için Fmerkezcil <= Fsürtünme olması gerekli. Eğer fazla ivmelenirseniz, yeterli merkezcil ivme sağlanamaz ve savrulursunuz (dönemezsiniz).
Merhabalar düşey virajla ilgili bir sorum olacak:
Şimdi virajın en alt noktasında demişiz ki agırlık ile tepki kuvvetinin farkından dolayı merkezcil kuvvet oluşur peki zaten ağırlık ve tepki kuvveti birbirine eşit ve zıt yönlü değil mi biz burda nasıl bir merkezcil kuvvetten söz edebiliyoruz ki ?
En alt noktada tepki kuvveti ağırlıktan fazla, eşit değil. N = G + Fmerkezcil
Virajda dönen bir araç güvenli dönüş hız sınırını aştığında araca merkez doğrultusunda etki eden fs etki etmeye devam eder mi? Çözdüğüm bir soruda Vmax aşıldığında cismin hız vektörü doğrultusunda ilerleyeceği söylenmiş anlayamadım. Cevaplarsanız çok sevinirim.
Araç kayar demek bu, sürtünme kuvveti yeterli merkezcil kuvveti sağlayamaz. Bu nedenle eğer hiç sürtünme kalmaz diye farz edersek araç, çevrilen bir ipten kopan taş gibi çembersel yörüngeye dik son hız yönünde hareket eder.
Öncelikle cevap verdiğiniz için çok teşekkürler. Sürtünme kuvveti yeterli merkezcil kuvveti sağlayamadığında cisim yarıçapını büyütmeye çalışır sonuçta da savrulur diye düşündüm. Verdiğiniz cevaptan fs yetersiz kaldığında merkeze doğru hiç fs kalmaz diye farz mı ediyoruz yoksa gerçekten kalmıyor mu anlayamadım. Gerçekte de fs sayesinde düzgün çembersel hareket yapan bir cisim Vmax aşıldığında fs hala etki ederken dışa doğru savrulur mu yoksa merkezde etki eden fs ortadan kalkar ve verdiğiniz iple bağlı cisim örneğindeki cisim gibi hız doğrultusu dışında etki eden kuvvet olmadığı için hız vektörü doğrultusunda mı hareket eder?
Aslında bir miktar sürtünme kuvveti kalır. Bu nedenle tam olarak çembere teğet savrulmaz. Ama artık çembersel hareket de yapamaz.
basit hormanik hareket ne zamangelecek hocam ,çok güzel anlatıyorsunuz teşekkür ederiz
Sürtünme kuvveti ile hız attırıldığında araç merkeze yaklaşabilir mi
Ne kadar artırıldıklarına bağlı.
Hocam 12.sınıf içeriklerinin devamı ne zamana hazır olur. Bilgilendirirseniz çok sevinirim.
11. sınıfı bitirmem lazım önce. MEB’in kitaplarından biri gayet iyi, öneririm.
gerçekten eksiksiz ve mantığıyla anlatıyorsunuz, kusursuz.
lütfen devamı gelsin
tepki kuvveti nasıl ağırlıktan fazla olabiliyor , bunun sebebi nedir , normalde hep ağırlık doğrultusundaki tepki kuvvetinin ağırlığa eşit olduğunu söylerdik
Yüzeyin tepki kuvveti (N), yüzeyin yüzeye dik olarak uyguladığı kuvvettir. Eğik virajda tepki kuvveti yüzeye dik ama ağırlığa eşit değil, ama ağırlık doğrultusundaki bileşeni ağırlığa eşit. Eğik düzlemde de yüzeyin tepki kuvveti ağırlığa eşit değil.
Harika anlatım ellerine emeğinize sağlık