Eğik atış hareketi nedir? Örnek soru çözümleri

İki boyutta hareketi incelemeye eğik atış ile devam ediyoruz. Eğik atış yatay düzlemle açı yapacak şekilde atılan bir cismin hareketidir. Cisim yataydan yukarı yönlü bir açı yapacak şekilde atılıyorsa buna yukarı yönlü eğik atış, aşağı yönlü atılıyorsa aşağı yönlü eğik atış ya da pike atış denir. Biz önce yukarı yönlü eğik atışa bakalım. Eğik atış formülleri de incelediklerimiz arasında olacak.

Aşağıdaki animasyonda yatayla 60° açı yapacak şekilde bir ilk hızla atılan bir topu gösteriyor. Tıpkı yatay atış hareketinde olduğu gibi, hava direncini ihmal ettiğimizde, eğik atılan cisim hem yatay hem de düşey doğrultuda aynı anda hareket eder, yani bileşik hareket yapar. Öyleyse eğik atış hareketini anlamamız için yatay ve düşey boyuttaki hareketleri ayrı ayrı incelemeliyiz.

Yatay boyutta eğik atış hareketi

Eğik atış hareketinde yatay boyuttaki hareketi anlamak için x-ekseni boyunca hız vektörüne dikkatlice bakmamız gerekiyor. Yukarıdaki animasyonda cisim atıldığı andan itibaren yatay hızının değişmediğini görebildiniz mi? v_x sağa doğru ve büyüklüğü sabit, cismin yeri değişse bile yatay yöndeki hızının büyüklüğü değişmiyor. Bu nedenle cisim bir boyutta sabit hızlı hareket (ya da düzgün doğrusal hareket) yapıyor.

Şimdi aşağıdaki animasyona bakın. Üstteki mavi top yukarı yönlü eğik atış hareketi yapıyor. Alttaki kırmızı top sabit hızlı yani düzgün doğrusal hareket yapıyor. Her iki topun aynı anda harekete geçtiklerini varsayarak, ikisinin de yatayda aldıkları yolun (yer değiştirmelerinin) hareketleri boyunca tüm zamanlarda birbirine eşit olduğunu görüyoruz.

O zaman eğik atışın yatay boyuttaki konum, hız ve zaman grafikleri düzgün doğrusal hareketle aynı olmalı. Ayrıca bu grafiklerin yatay atışın yatay boyuttakilerle de aynı olduğunu fark etmiş olmalısınız.

Eğik atışın yatay boyutta konum zaman grafiği: (Eğim hızı veriyor.)

Eğik atışın yatay boyutta hız zaman grafiği: (Grafiğin altında kalan alan alınan yolu, eğimi ivmeyi veriyor.)

Eğik atışın yatay boyutta ivme zaman grafiği: (Hız sabit demek.)

Eğik atışta yatay yönde hız neden değişmiyor? Çünkü, hava direncini ihmal ediyoruz, dolayısıyla, hareketi esnasında cisme yatay yönde etkiyen herhangi bir kuvvet yok. Net kuvvet sıfırsa, ivme de sıfır olmak zorunda (Newton’un ikinci hareket kanunu F_net = ma). İvme sıfır olduğuna göre hız sabit, çünkü ivme zamana göre hız değişimi demek.

Öyleyse eğik atışta yatay boyutta hareket denklemlerimiz yani formüllerimiz bir boyutta sabit hızlı hareket ile aynı. Hızın yatay bileşeninin v_0x = v₀ cosθ olduğuna dikkat edin. θ açısı ilk hız vektörünün yatayla yaptığı açı. t ise uçuş süresi.
a = 0 \space m/s^2

v = v_{0x} = v_0 cos \theta \Delta x = v_{0x}t; \Delta x = v_0 cos \theta t

Cismin x-eksenindeki maksimum yer değiştirmesi yani menzili:
x_{menzil} = v_{0x}t_{u} = v_0 cos \theta t_{u}

Düşey boyutta eğik atış hareketi

Yazının başındaki animasyona tekrar bakın. Bu kez düşeydeki yani yukarı ve aşağı yönlü harekete dikkat edin. Düşeyde (yani y-ekseninde) hız vektörünün uzunluğu nasıl değişiyor? Cisim yukarı çıkarken kısaldığını, tepe noktasına (h_maksimum diyoruz buna) ulaştığında sıfır olduğunu, aşağı inerken uzadığını görmüş olmalısınız. Düşey boyuttaki hareketin yukarı yönlü düşey atış hareketi olduğunu fark edebildiniz mi?

Aşağıdaki animasyona dikkatlice bakın. Sağdaki mavi top eğik atış hareketi yapıyor. Soldaki kırmızı top yukarı yönlü düşey atış hareketi yapıyor. Her iki top aynı anda harekete geçtiyse, ikisinin de yerden yükseklikleri hareketleri boyunca tüm zamanlarda birbirine eşit.

Yukarı yönlü eğik atış hareketi, düşey boyutta, niçin yukarı yönlü düşey atış hareketiyle aynı? Çünkü cisim sadece yer çekimi (dünyanın kütle çekimi) kuvveti etkisi altında (hava direncini ihmal ediyoruz). Yani cisme uygulanan net kuvvet cismin ağırlığına eşit. Bu yüzden düşey doğrultudaki ivmesi a_y = g, yani yer çekimi ivmesine eşit. Bu nedenle, eğik atılan cisim düşey yukarı yönde çıkarken düşey hızı düzgün azalır ve bir süre sonra sıfır olur. Artık cisim daha fazla yükselemez; çıkabileceği maksimum yüksekliğe (tepe noktasına) ulaşmış olur. Cismin çıkabileceği maksimum yükseklikte sadece yatay hızı kalır. Bu noktadan sonra cismin hareketi yatay atış hareketinin aynısıdır.

Öyleyse yukarı yönlü eğik atışta düşey boyuttaki konum, hız ve ivme grafikleri yukarı yönlü düşey atış ile aynı.

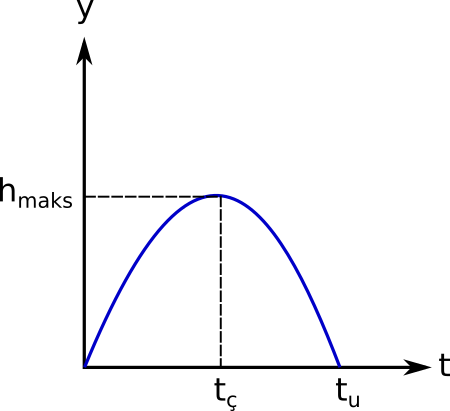
Eğik atışın düşey boyutta konum zaman grafiği: (h_maks tepe noktası yani maksimum yükseklik, t_ç tepe noktasına çıkış süresi t_u uçuş süresi demek. t_u = 2t_ç yani uçuş süresi tepe noktasına çıkış süresinin iki katına eşit.)

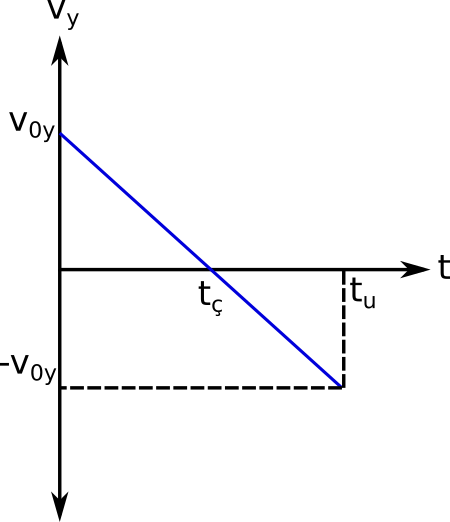
Eğik atışın düşey boyutta hız zaman grafiği:

Eğik atışın düşey boyutta ivme zaman grafiği:

Öyleyse yukarı yönlü eğik atış için hareket denklemlerimiz yani formüllerimiz yukarı yönlü düşey atış ile aynı:

a = g; a = 10 \space m/s^2
v_y = v_{0y} - gt
h = v_{0y}t - \frac{1}{2}gt^2

h_{maks} = \frac{1}{2}gt_c^2
Zamansız hız formülümüz de:
v_y^2 = v_{oy}^2 - 2gh

Eğik atışta hız vektörü ve büyüklüğü

Aşağıdaki resimde bir top eğik olarak atılıyor (hava direnci ihmal ediliyor). Topun bulunduğu noktalarda sırasıyla 0, t, 2t, 3t ve 4t anlarında fotoğraf çekildiğini varsayalım.

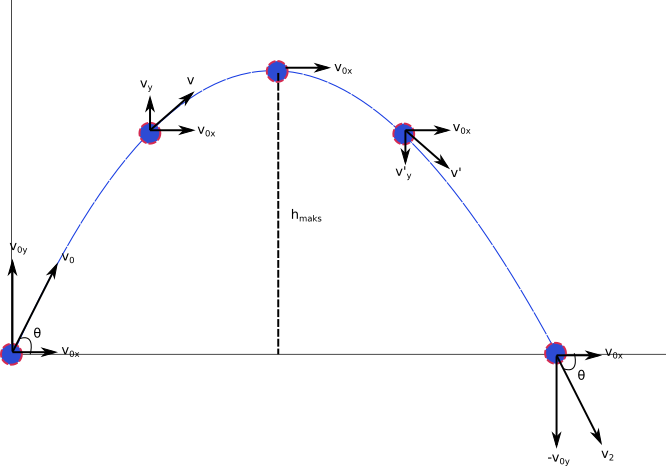
• Topun ilk hızı v₀, yatayla yaptığı açı θ (bu t=0 anı). Yataydaki hız v_0x = v₀cosθ, düşeydeki hızı v_0y = v₀sinθ
• t anındaki hızı v. Yataydaki hızı değişmiyor. v_x = v_0x = v₀cosθ. Düşeydeki hızı ise: v_y = v_0y – gt. = v₀sinθ – gt. Hız vektörü yatay ve düşey hız vektörlerinin bileşeni, büyüklüğünü de pisagor teoreminden bulabiliriz.

v^2 = v_x^2 + v_y^2 v^2 = (v_0cos \theta)^2 + (v_0sin \theta - gt)^2

• 2t anındaki hızı sadece yatay hız, v_0x. Bu noktada maksimum yüksekliğe yani tepe noktasına ulaşıyor. Yalnızca yatay hız kalıyor. Ama düşey hızın sıfır olmasından şunu elde edebiliriz:

v_y = 0 ; 0 = v_{oy} - g(2t); v_{oy} = 2gt; v_0sin \theta = 2gt

• 3t anında, yükseklik t anındaki yüksekliğe eşit. Hız v’, yatay hızın yönü ve büyüklüğü değişmiyor v_0x = v₀cosθ. Düşey hız ise artık eksi yönlü (aşağı doğru). Düşey hızın büyüklüğü v_y = v_0y – 3gt. = v₀sinθ – 3gt. Hız vektörünün şiddetini bulabiliriz:

v'^2 = v_x^2 + v_y^2 v'^2 = (v_0cos \theta)^2 + (v_0sin \theta - 3gt)^2

Bu durumu dikkatlice t anıyla kıyaslayalım:

v^2 = (v_0cos \theta)^2 + (2gt - gt)^2 \space (t \space ani)
v'^2 = (v_0cos \theta)^2 + (2gt - 3gt)^2 \space (3t \space ani)
Buradan v = v’ olduğunu görüyoruz. Bunu genellersek, eğik olarak atılan bir cismin yükselirken ve düşerken aynı yüksekliklerdeki hız büyüklükleri (süratleri) eşittir.

• 4t anında cisim yere düşüyor. Yatay hız değişmiyor, düşey hız ise -v_0y. Yani yere çarpma hızının büyüklüğü atılma hızıyla aynı.
• Eğik atılan cisimlerin yörüngesinin (hareketleri boyunca izledikleri yolun) parabolik olduğunu da görüyoruz.
• Tepe noktasına çıkış süresinin, tepe noktasından yere iniş süresine eşit olduğunu ve bu ikisinin de uçuş süresinin yarısına eşit olduğunu da görüyoruz.
• Tepe noktasından sonra cismin yatay atış hareketiyle aynı hareketi yaptığını da görüyoruz.

Örnek soru 1:

Bir cisim yatayla 37° açı yapacak biçimde, 20 m/s büyüklüğünde ilk hızla yukarı yönlü atılmaktadır. Buna göre cismin:

a) Tepe noktasındaki (maksimum yükseklikteki) hızının büyüklüğü kaç m/s olur?
b) Tepe noktasına çıkış süresi kaç s olur?
c) Uçuş süresi kaç s olur?
d) Çıkabileceği maksimum yükseklik kaç m olur?
e) Menzili kaç m olur?

(sin 37° = 0,6; cos 37° = 0,8 ve g = 10 m/s² alın).

Çözüm

a) Cisim yukarı yönlü eğik atış yapıyor. Tepe noktasındaki hızının cismin ilk hızının yatay bileşenine eşit olduğunu biliyoruz. Öyleyse:
v_x = v_{0x} = v_0 cos \theta

v_0 = 20 \space m/s; v_x = (20 \space m/s)cos 37^\circ
v_x = (20 \space m/s)(0,8) = 16 \space m/s

b) Tepe noktasına çıkış süresini düşey hızdan bulabiliriz. Düşey hızın sıfır olduğu an tepe noktasına ulaşılan an demek.
v_{0y} - gt = 0 ; v_0 sin \theta = gt_c

(20 \space m/s) sin 37^\circ = (10 \space m/s^2)t_c t_c = \frac {(20 \space m/s)0,6}{(10 \space m/s^2)} = 1,2 \space s

c) Uçuş süresinin çıkış süresinin iki katı olduğunu biliyoruz: t_u = 2t_ç
t_u = 2 \times 1,2 \space s = 2,4 \space s
d) Maksimum yüksekliği çıkış süresinden bulabiliriz:
h = \frac{1}{2}gt^2_c

h = \frac{1}{2}(10 \space m/s^2)(1,2 \space s)^2 = 7,2 \space m

e) Menzilin yani yatayda alınan toplam yolun yatay hızla uçuş süresinin çarpımı olduğunu biliyoruz:
x = v_{0x}t_u = (16 \space m/s)(2,4 \space s) = 38,4 \space m

Örnek soru 2:

Hava direncinin ihmal edildiği ortamda bir cisim aynı ilk süratle fakat sırasıyla yatayla θ₁ = 30°, θ₂ = 45° ve θ₃ = 60° açı yapacak biçimde yukarı yönlü atılıyor. Cismin menzil uzaklıkları (yatayda alabilecekleri en uzun yol) sırasıyla x₁, x₂ ve x₃ olduğuna göre, bu uzaklıklar büyükten küçüğe nasıl sıralanır? (sin 30° = cos 60° = 0,5; sin 60° = cos 30° = √3/2; sin 45° = cos 45° = √2/2)

Çözüm

Menzilleri hesaplamadan önce genel menzil formülü elde edebilecek miyiz bir deneyelim:
x = v_0 cos \theta t_{u}
t_u = 2t_c; t_{c} = \frac{v_0 sin \theta}{g}; t_u = 2\frac{v_0 sin\theta}{g}
x = \frac{v_0^2}{g} (2sin \theta cos \theta)

Trigonometriden :
sin (2\theta) = 2sin \theta cos \theta

Öyleyse:
x = \frac{v_0^2}{g} sin 2\theta
İlk hızlar aynı v₀, sin 2θ değeri en yüksek olan açı en büyük olan olmalı.

• θ = 30° için 2θ = 60° => sin 60° = √3/2
• θ = 45° için 2θ = 90° => sin 90° = 1
• θ = 60° için 2θ = 120° => sin 120° = √3/2

Demek ki en uzağa 45° ile atılan cisim gider, 30° ve 60° ile atılan cisimler daha az ama birbirine eşit mesafe giderler.

x₂ > x₁ = x₃

Eğik atış ile ilgili kazanımlar

2018- 11.1.5.1. Atış hareketlerini yatay ve düşey boyutta analiz eder.
Öğrencilerin deney yaparak veya simülasyonlarla atış hareketlerini incelemeleri ve yorumlamaları sağlanır.
2018-11.1.5.2. İki boyutta sabit ivmeli hareket ile ilgili hesaplamalar yapar.