Düzgün Doğrusal Hareket Nedir? Konum Hız Zaman Grafikleri

Hareket basit de olabilir karmaşık da. En kolay incelenebilecek olan hareket çeşidi bir doğru boyunca, yani bir boyutta, olandır. Günlük hayatımızdan örnek vermek gerekirse yürüyen merdivenler, trenler ve asansörler doğrusal hareket yapar. Düzgün doğrusal hareket ya da sabit hızlı hareket, hareketi boyunca bir cismin hızının sabit olması, hiç değişmemesidir.

Sabit hız nedir?

Hız ve sürat arasındaki farkı hatırlayarak, hızın sabit olmasının hem büyüklüğünün hem de yönünün zamana göre değişmemesi anlamına geldiğine dikkat etmeliyiz. Sabit hızda ortalama hız ve anlık hız birbirine eşittir, bu nedenle bu durumda yalnızca hız diyoruz.

Sabit hızla harekette eşit sürelerdeki yer değiştirmeler aynıdır. Bir örnekle açıklayalım.

Örnek Soru 1

Avustralyalı bir belgeselci bir kangurunun doğrusal bir yol boyunca ilerlerken ikişer saniye aralıklarla fotoğraflarını çekiyor. Bu fotoğrafların birleştirilmiş hali şekilde gösterildiğine göre, kanguru düzgün doğrusal hareket yapmış mıdır?

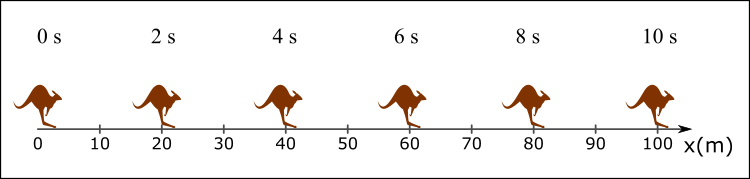
Çözüm:

Kangurunun hareketini anlamak için konum – zaman grafiğini çizeceğiz.

Konum – Zaman Grafiği

Fizikte hareketi göstermenin önemli bir yolu grafik kullanmaktır. Konum – zaman grafiğini çizebilmek için önce kangurunun hangi zamanda hangi konumda olduğunu gösteren bir tabloya ihtiyacımız var.

Zaman (s)	Konum (m)
0	0
2	20
4	40
6	60
8	80
10	100

Bu değerleri yatay ekseni zamanı t(s), düşey ekseni konumu x(m) gösteren grafiğe noktalar olarak yerleştirelim. t = 0 s anında kanguru x=0 m konumunda, t = 2 s de x = 20 m konumunda. Konum ve zaman bilgisini her zıplama için grafikte bir nokta olarak gösteriyoruz.

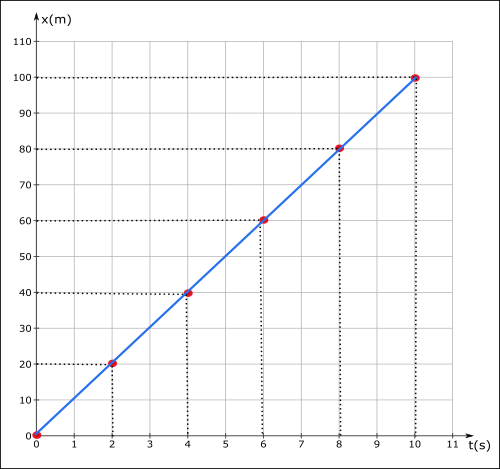
Bütün noktaları bir doğru ile birleştirebiliyoruz, mavi çizgi ile, buna konumun zamana göre fonksiyonu diyoruz x(t). Düzgün doğrusal harekette konum – zaman grafiğindeki konumun zamana göre fonksiyonu her zaman düz bir çizgidir (eğimi sabittir), eğri değildir.

Kangurunun zıplamaları arasındaki yer değiştirmeleri ve geçen süreyi hesaplarsak her zıplama arasındaki hızı bulabiliriz. Tüm hesaplamalarımızda yer değiştirme ve hız tanımlarından faydalanacağız, hatırlayalım:

\Delta{\vec{x}} = \vec{x}_{son} - \vec{x}_{ilk} \Delta{t} = {t}_{son} - {t}_{ilk} \vec{v} = \frac{\Delta{\vec{x}} }{\Delta{t}}

Şimdi hızı hesaplamak için bir tablo daha yapalım. Bu tabloda ilk sütunda yer değiştirme, ikinci sütunda zaman aralığı hesaplanıyor. Son sütunda her zıplamadaki hız gösteriliyor, yer değiştirmenin geçen zaman aralığına oranı hesaplanıyor.

Δx (m)	Δt (s)	v (m/s)
20 – 0 = 20	2 – 0 = 2	20 / 2 =10
40 – 20 = 20	4 – 2 = 2	20 / 2 =10
60 – 40 = 20	6 – 4 = 2	20 / 2 =10
80 – 60 = 20	8 – 6 = 2	20 / 2 =10
100 – 80 = 20	10 – 8 = 2	20 / 2 =10

Görüldüğü gibi bu kangurunun hızı 0 – 10 saniye aralığında hep 10 m/s olmuş, yani sabitmiş. Kanguru eşit zaman aralıklarında eşit miktarda yer değiştirmiş. Dolayısıyla kanguru düzgün doğrusal hareket yapmış.

Hız – Zaman Grafiği

Kangurunun hareketini konum – zaman grafiğiyle gösterdikten sonra bir de hız – zaman grafiğiyle gösterelim. Bunun için zaman ve hesapladığımız hız değerlerimizi bir tabloya yerleştirelim. t = 0 anında kangurunun hızının 10 m/s olduğunu konum – zaman grafiğinden öngörüyoruz.

Zaman (s)	Hız(m/s)
0	10
2	10
4	10
6	10
8	10
10	10

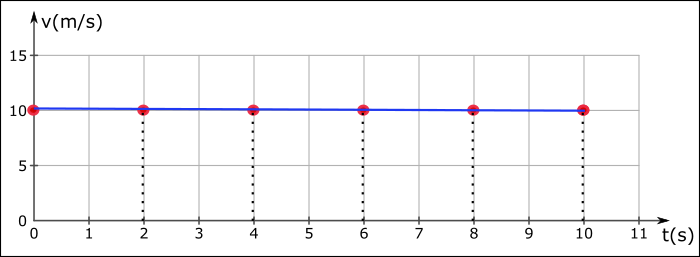
Veri tablosundaki noktaları yerleştirdiğimizde kangurunun hız – zaman grafiği yukarıdaki gibi oluyor:

Düzgün doğrusal hareketin hız -zaman grafiğinde hızı gösteren mavi doğru hızın zamana göre fonksiyonudur v(t). Hızın zamana göre fonksiyonu düzgün doğrusal harekette hep zaman eksenine paraleldir, eğimi her zaman sıfırdır. Çünkü hız zamana göre değişmemektedir.

Hız – zaman grafiğini kullanarak kangurunun yer değiştirmesini bulabiliriz. Hız doğrusunun altında kalan alan bize yer değiştirmeyi verir.

\Delta\vec{x} = \vec{v} \times \Delta{t}

Herhangi bir zaman aralığı için yer değiştirmeyi hesaplayabildiğimize göre eğer hız – zaman grafiğini biliyorsak, konum – zaman grafiğini de elde edebiliriz. Tersi de geçerlidir, eğer konum – zaman grafiğini biliyorsak, hız – zaman grafiğini çizebiliriz.

Örnek Soru 2

Bir patenci 3 saniye boyunca 4 m/s sabit hızla hareket ediyor. Sonra aniden duruyor ve 2 saniye bekliyor. Son olarak da yönünü değiştirip -2 m/s sabit hızla 5 saniye ilerliyor. Patencinin başlangıç noktasına göre konumu nedir?

Çözüm:

Patencinin hızları ve zaman aralıkları soruda verildiği için hız – zaman grafiğini çizerek başlayalım.

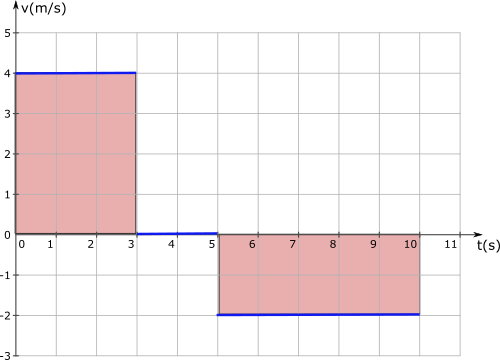
Grafikte patencinin hareketinin üç aşaması gösteriliyor. Yer değiştirmeleri hesaplayalım, sonra konum – zaman grafiğini çizelim.

• 0 – 3 saniye arasındaki hızı 4 m/s olduğuna göre x = 4 doğrusuyla x-ekseni arasında kalan dikdörtgenin alanı yer değiştirmeye eşittir. \Delta{x}_{1} = 4 \space m/s \times 3 \space s = 12 \space m

Başlangıç konumunu x = 0 alırsak konumu x(3 s) = 12 m olur.

• 3 – 5 saniye arasında hız sıfırdır. Yani patenci durmuştur, yer değiştirmemiştir. \Delta{x}_2 = 0 \space m

Konumu aynı kalmıştır, x (5 s) = 12 m.

• 5 – 10 saniye arasında patenci geri dönmüştür. x = -2 doğrusuyla x-ekseni arasında kalan dikdörtgenin alanı yer değiştirmeyi verir. \Delta{x}_{2} = -2 \space m/s \times 5 \space s = -10 \space m

Patencinin son konumu x(10 s) = 12 m – 10 m = 2 m olur.

Şimdi de konum – zaman grafiğini çizelim.

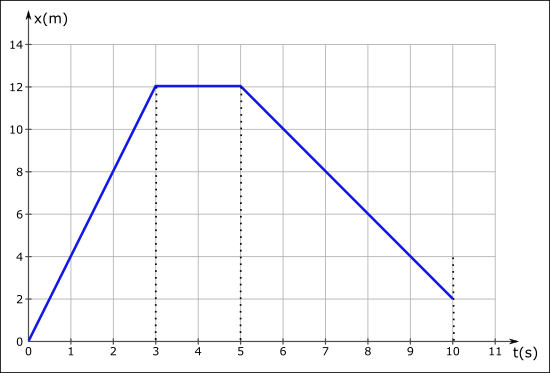
Düzgün doğrusal harekette zamana göre hız değişimi, yani ivme, sıfırdır. Bu nedenle düzgün doğrusal hareket ivmesiz hareket de denir.

Düzgün Doğrusal Hareket Problemleri

1. A ve B karıncaları aynı konumdan başlayarak doğrusal bir borunun içinde aynı yöne doğru sabit hızla yarışıyorlar. A karıncasının hızı 7 cm/s, B karıncasının hızı 9 cm/s olduğuna ve yarış 120 saniye sürdüğüne göre, yarışı hangi karınca kaç metre farkla kazanır?
2. Ahmet ve Zeynep doğrusal bir yolda aynı yönde sabit hızla koşuyorlar. Koşmaya başladıkları anda Ahmet, Zeynep’e göre 40 m öndedir. Ahmet’in hızı 2 m/s, Zeynep’in hızı 4 m/s olduğuna göre (a) 15 saniye sonra kim öndedir? (b) Ahmet’in ve Zeynep’in konum – zaman grafiğini çizin.
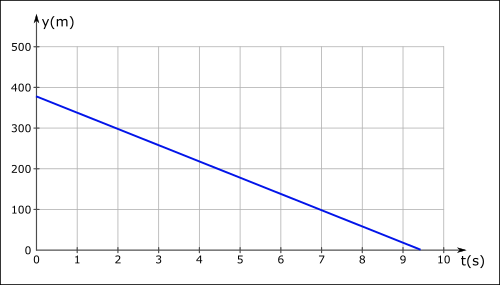
3. Aşağıda sabit hızla düşen bir yağmur damlasının konum – zaman grafiği verilmiştir. Buna göre yağmur damlasının hızı kaç m/s’dir?

Düzgün Doğrusal Hareket Kazanımları

9.3.1.4. Düzgün doğrusal hareket için konum, hız ve zaman kavramlarını ilişkilendirir.

• Öğrencilerin deney yaparak veya simülasyonlarla veriler toplamaları, konum-zaman ve hız-zaman grafiklerini çizmeleri, bunları yorumlamaları ve çizilen grafikler arasında dönüşümler yapmaları sağlanır.
• Öğrencilerin grafiklerden yararlanarak hareket ile ilgili matematiksel modelleri çıkarmaları ve yorumlamaları sağlanır.

Düzgün Doğrusal Hareket Test

Hareket Testi: Temel Kavramlar ve Grafikler