Yatay atış hareketi nedir? Örnek soru çözümleri

Atışlar konusuna iki boyutta hareket ile devam edeceğiz. İki boyutta hareketi incelemeye yatay atış ile başlıyoruz. İki boyutta demek hareketin bileşik hareket olduğu anlamına gelir. Yani bir binadan yatay atılan bir cisim hem yatay hem de düşey boyutlarda aynı anda hareket eder, biz bu iki hareketin birleşmiş halini gözlemleriz. Yatay atış hareketinde bu durumu anlatmak için aşağıdaki animasyonu kullanalım.

Öncelikle hava direncini ihmal ettiğimizi kabul edeceğiz. Yukarıdaki animasyonda bir bal kabağı 7 metre yüksekliğindeki bir kuleden yatayla 0 derece açı yapacak şekilde, ilk hızı 10 m/s olarak fırlatılıyor. Bal kabağının izlediği yolun mavi renkle gösterilen bir eğri olduğunu görmüş olmalısınız. Şimdi bu bileşik hareketi şöyle görmeye çalışalım: Bal kabağı hem sağa doğru hem de aşağı doğru hareket ediyor. Sağa doğru hareketini x-ekseninde, aşağı doğru hareketine y-ekseninde inceleyebiliriz. Yatay ve düşey boyuttaki hareket de birbirinden bağımsız, biri diğerini etkilemiyor.

Yatay boyutta yatay atış hareketi

Animasyondaki yatay boyuttaki hareketi nitel olarak anlamanın bir yolu x-eksenindeki hız vektörüne bakmak. v_x sağa doğru ve büyüklüğü sabit, cismin yeri değişse bile yatay yöndeki hızının büyüklüğü değişmiyor. İlk hızı sadece yatayda 10 m/s olduğuna göre hareketi boyunca cismin yataydaki v_x hızı hep 10 m/s olarak kalıyor. Bunu tanımış olmalısınız: bir boyutta sabit hızlı hareket (ya da düzgün doğrusal hareket).

Şimdi aşağıdaki animasyonu dikkatlice inceleyin. Üstteki mavi top düzgün doğrusal hareket yani sabit hızlı hareket yapıyor. Alttaki kırmızı top yatay atış hareketi yapıyor. Her iki topun aynı anda harekete geçtiklerini varsayarak, ikisinin de yatayda aldıkları yolun (yer değiştirmelerinin) hareketleri boyunca tüm zamanlarda birbirine eşit olduğunu görüyoruz.

Öyleyse yatay atışın yatay boyuttaki konum, hız ve zaman grafikleri sabit hızlı hareket ile aynı olmalı.

Konum zaman grafiği yatay boyutta şöyle:

Hız zaman grafiği yatay boyutta şöyle:

İvme zaman grafiği yatay boyutta şöyle:

Neden yatay yönde hız değişmiyor? Çünkü, hava direncini ihmal ettiğimiz için, hareketi süresince cisme yatay yönde etkiyen herhangi bir kuvvet yok. Newton’un birinci hareket kanununa (eylemsizliğe) göre bir cismin hızı (büyüklüğü ve yönü) değişmiyorsa, o cisme etkiyen net kuvvet sıfırdır. Net kuvvet sıfırsa, ivme de sıfır olmak zorunda (Newton’un ikinci hareket kanunu F_net = ma). İvme sıfır olduğuna göre hız sabit, çünkü ivme zamana göre hız değişimi demek.

Öyleyse hareket denklemlerimiz yani formüllerimiz bir boyutta sabit hızlı hareket ile aynı:
a = 0 \space m/s^2
v = v_0
\Delta x = v_0t

Düşey boyutta yatay atış hareketi

Şimdi bu yazının başındaki animasyona tekrar bakmanız gerekiyor. Bu kez düşeydeki yani aşağı yönlü harekete odaklanmalısınız. Özellikle hızın y-eksenindeki bileşenine dikkat etmelisiniz. Cisim aşağı düştükçe, v_y vektörünün uzadığını yani büyüklüğünün değiştiğini fark etmiş olmalısınız. Düşey boyuttaki hareketin aslında serbest düşme olduğunu da fark edebildiniz mi? (Yine hava direncini ihmal ediyoruz.) Aşağıdaki animasyona dikkatlice bakın. Sağdaki mavi top serbest düşme hareketi yapıyor. Soldaki kırmızı top yatay atış hareketi yapıyor. Her iki topun aynı anda harekete geçtiklerini varsayarak, ikisinin de yerden yüksekliklerinin hareketleri boyunca tüm zamanlarda birbirine eşit olduğunu görüyoruz.

Yatay atış hareketi düşey boyutta neden serbest düşme hareketiyle tamamen aynı peki? Çünkü cisim sadece yerçekimi (dünyanın kütle çekimi) kuvveti etkisi altında. Yani cisme uygulanan net kuvvet cismin ağırlığına eşit. Bu yüzden düşey doğrultudaki ivmesi a_y = g yani yerçekimi ivmesine eşit.

Serbest düşme hareketinin düşey doğrultuda sabit ivmeli hareket olduğunu biliyoruz. (Hatırlamıyorsanız serbest düşmeyi tekrar okuyun derim.) Öyleyse yatay atıştaki düşey boyuttaki konum, hız ve ivme grafikleri serbest düşme ile aynı.

Konum zaman grafiği düşey boyutta şöyle:

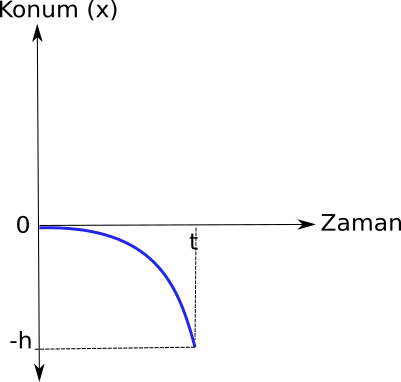
Hız zaman grafiği düşey boyutta şöyle:

İvme zaman grafiği düşey boyutta şöyle:

Öyleyse hareket denklemlerimiz yani formüllerimiz bir boyutta sabit ivmeli hareket (yani serbest düşme) ile aynı:
a_y = g = 10 \space m/s^2

v_y = gt

h = \frac{1}{2}gt^2
Zamansız hız formülü de:
v_y^2 = 2gh \space; \space v_y = \sqrt{2gh} \space

Yatay atışta hız vektörü ve büyüklüğü

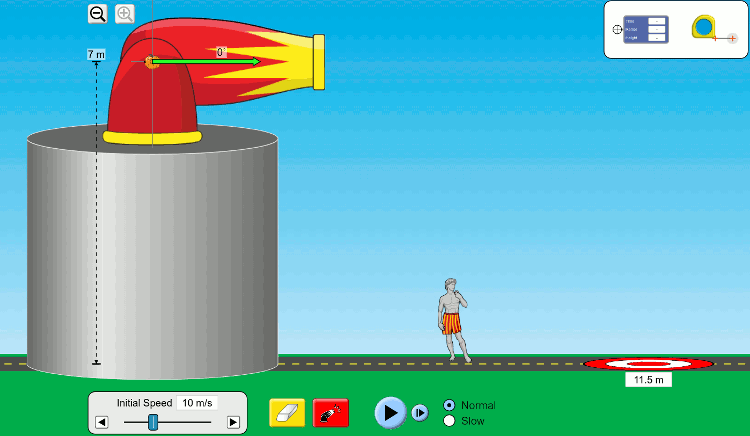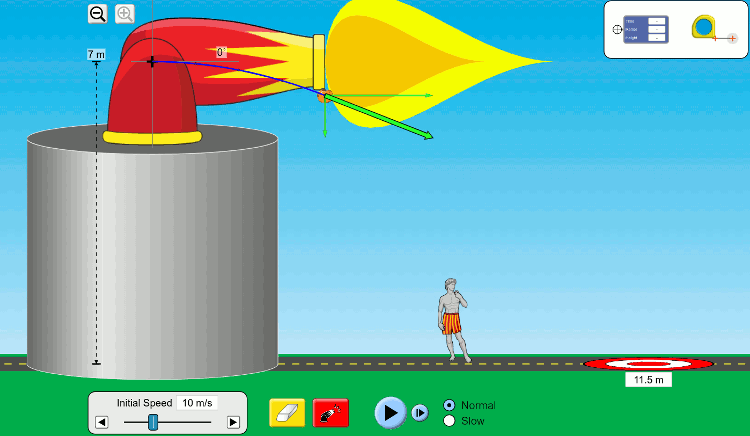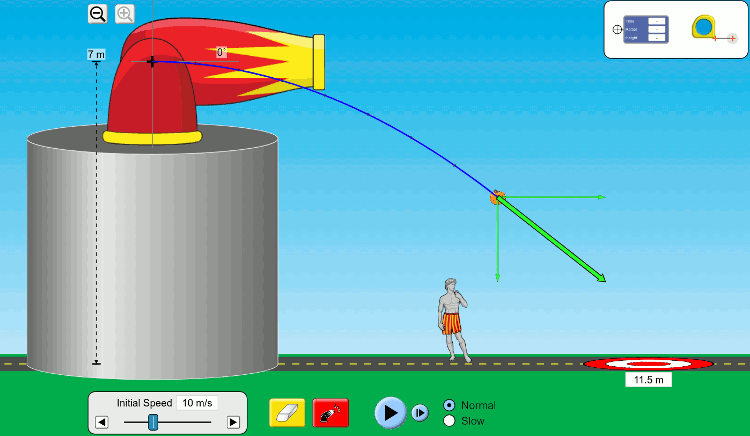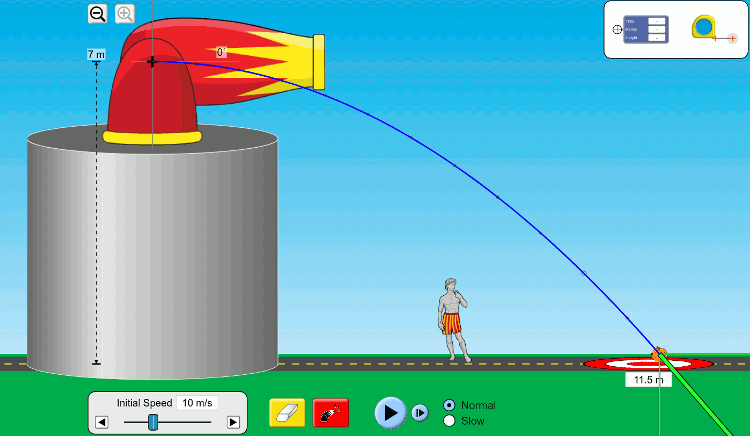
Yatay atışın yatay ve düşey boyutta iki hareketin birleşimi olduğunu öğrendik. Yatay ve düşey hızların birbirinden bağımsız olduğunu ve nasıl hesaplayabileceğimizi de biliyoruz. Şimdi sıra atış hareketinin herhangi bir zamanında hız vektörünün bileşkesini bulmaya geldi. Aşağıdaki resimde yatay atışın farklı anlarındaki hız vektörü gösteriliyor.

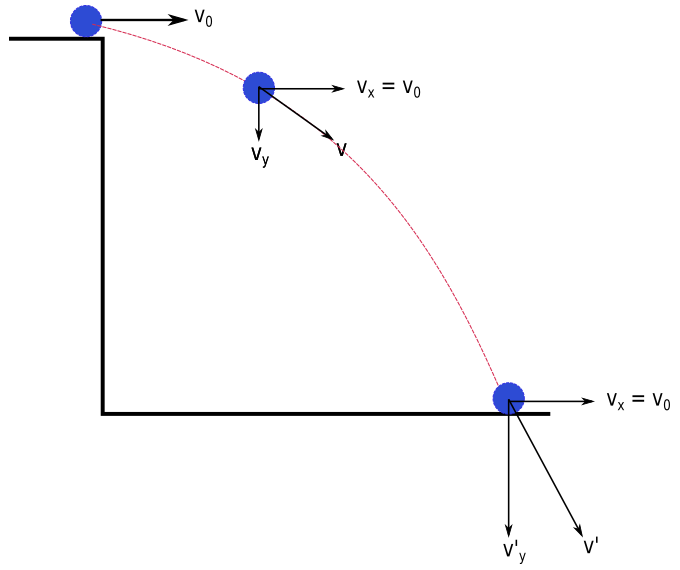
• Atışın başlangıcı t=0 dersek, hız vektörü sadece yatay hız vektörüne eşit \vec{v} = \vec{v_x} = \vec{v_0}, büyüklüğü de v = v₀.
• t = t diye bir an aldığımızda, hız vektörü hem yatay hem de düşey hız vektörlerinin vektörel toplamına eşit. Yani:
  \vec{v} = \vec{v_x} + \vec{v_y}
  Büyüklüğü de pisagor teoreminden bulunabilir (çünkü x ve y eksenleri birbirine dik):
  v^2 = v_0^2+v_y^2; \space v = \sqrt{v_0^2+v_y^2}
• Yere düştüğü ana t = t’ dersek, yere çarpma hızı v’ yine dik bileşenlerin vektörel toplamına eşit:
  \vec{v'} = \vec{v_0} + \vec{v'_y}
  Büyüklüğü de pisagor teoreminden bulunabilir (çünkü x ve y eksenleri birbirine dik):
  v'^2 = v_0^2+v'^2_y; \space v' = \sqrt{v_0^2+v'^2_y}

Yatay atışla ilgili vardığımız sonuçlar

• Atılan cismin izlediği yol paraboliktir.
• Hareket bileşiktir. Ama birbirinden bağımsız yatay ve düşey boyutlara ayrılıp incelenebilir.
• Yatay boyutta hareket düzgün doğrusal harekettir, hız sabittir, ivme sıfırdır.
• Düşey boyutta hareket serbest düşmedir, bir boyutta sabit ivmeli harekettir.
• Cismin uçuş süresini yerden yüksekliği (düşey boyut) belirler.
• Yatay hızın büyüklüğü cismin uçuş süresini etkilemez, sadece menzini (yatay düzlemde yere düşeceği yeri) değiştirir.
• Cismin herhangi bir noktadaki hızı yatay ve düşey hız vektörlerinin toplamıdır (vektör toplama olduğunu unutmayın).

Örnek soru 1:

Yüksekliği 80 m olan bir gökdelenden bir elma ilk hızı 20 m/s olacak şekilde yatay olarak atıldığında:

a) Elmanın uçuş süresi nedir?

b) Elmanın yatayda aldığı yol (menzili) nedir?

c) Elmanın yere çarptığı andaki hızının büyüklüğü (sürati) nedir?

(Hava direnci ihmal ediliyor, g = 10m/s² veriliyor)

Çözüm:

a) Yatay atış yapılmış. Elmanın uçuş süresinin düşeydeki hareketine bağlı olduğunu biliyoruz. Düşeyde elma serbest düşme yaptığına göre:

h = \frac{1}{2}gt^2
h = 80 m

80 = \frac{1}{2}10t^2 16 = t^2 t = 4 \space s

b) Elmanın yatayda düzgün doğrusal hareket yaptığını biliyoruz. Öyleyse aldığı yol:
x = v_0t

x = 20 (m/s) \times 4(s) = 80 \space m

c) Elmanın yere çarptığı andaki hızı yatay ve düşey hızlarının vektörel toplamı olduğunu biliyoruz:

v^2 = v_0^2 + v_y^2 v_y = gt; \space v_y = 10 \times 4 = 40\space m/s v^2 = 20^2 + 40^2; v^2 = 400 + 1600 = 2000 v = \sqrt{2000} = 20\sqrt{5} \space m/s = 44,7 \space m/s

Örnek soru 2:

125 m yükseklikten iki cisim aynı anda aynı yönde yatay olarak atılıyor. Birinci cismin ilk hızı 10 m/s, ikinci cismin ilk hızı 30 m/s olduğuna göre, cisimler yere çarptıklarında aralarındaki mesafe kaç metre olur? (Hava sürtünmesini ihmal edin, g = 10 m/s² alın.)

Çözüm

Cisimlerlin yatay atış yaptığını biliyoruz. İki cismin arasındaki mesafeyi bulmak için:
\Delta x = x_2 - x_1=v_2t - v1t = (v_2-v_1)t
Öyleyse tek yapmamız gereken cisimlerin uçuş süresini bulmak:
h=\frac{1}{2}gt^2
125 = \frac{1}{2}(10)t^2
t^2 = 25; t = \sqrt{25} = 5 \space s
Şimdi t’yi yerine koyarak iki cisim arasındaki mesafeyi hesaplayabiliriz:
\Delta x = (30 - 10)\times 5 = 20 \times 5 = 100 \space m

Yatay atış ile ilgili kazanımlar

2018- 11.1.5.1. Atış hareketlerini yatay ve düşey boyutta analiz eder.
Öğrencilerin deney yaparak veya simülasyonlarla atış hareketlerini incelemeleri ve yorumlamaları sağlanır.
2018-11.1.5.2. İki boyutta sabit ivmeli hareket ile ilgili hesaplamalar yapar.