Elektriksel Kuvvet ve Elektrik Alan: Örnek Sorular ve Çözümleri

Daha önce elektriksel kuvvet ve elektrik alanın ne olduğunu öğrenmiştiniz. Bu yazının amacı öğrendiklerinizi pekiştirmeniz için örnek sorular çözmek. Buradaki soruların çözümlerini anlamaya çalışın, ama asıl kendiniz çözerseniz öğrenirsiniz. Kısaca elektriksel kuvveti hatırlatalım: Elektrik yüklerinin birbirini çekmesine veya itmesiydi. k ortamın elektriksel geçirgenliği, q₁ ve q₂ sırasıyla iki cismin yükleri ve x aralarındaki mesafe olmak üzere şöyle gösteriliyordu:
\vec{F} = k\frac{q_1 q_2}{x^2}

Elektrik alanı da elektrik yükünün uzayın elektrik alan özelliğini bozması olarak tanımlamıştık. Bir yükün bir başka yükten haberi olması bu aracı alanla gerçekleşiyordu. Q yüklü bir cismin elektrik alanını, q₀ test yükü ile bulmak için şöyle tanımlıyorduk:
\vec{E} = \frac{\vec{F}}{q_0}

\vec{E} = k\frac{Q \cancel{q_0}}{\cancel{q_0}x^2} = k\frac{Q}{x^2}

Hem elektriksel kuvvetin hem de elektrik alanın vektörel büyüklükler olduğuna da dikkat edin. Elektriksel kuvvetin biriminin Newton (N), elektrik alanın biriminin de Newton/Coulomb (N/C) olduğunu da çıkarabiliriz.

Örnek soru 1: Elektriksel kuvveti kıyaslama

 

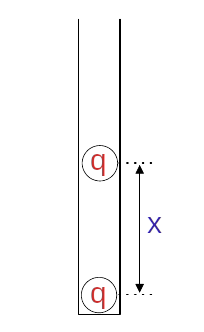
Şekildeki test tüpünün içine her birinin yükü q olan iki plastik top yerleştirilince aralarındaki mesafe x olduğunda toplar dengede kalıyor. Plastik topların yükleri iki katına çıkarılırsa dengede olduklarında aralarındaki mesafe kaç x olur?

Çözüm:

Öncelikle plastik topları noktasal parçacık olarak modelliyoruz. Sonra üstteki topun serbest cisim diyagramını çiziyoruz, bakalım üsünde hangi kuvvetler var?

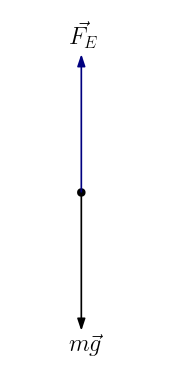
Üstteki top dengede, demek ki Newton’un Birinci Hareket Yasası’na göre net kuvvet sıfır olmalı yani cisim dengelenmiş kuvvetlerin etkisinde. Öyleyse:
\vec{F_E}-m\vec{g} = 0

|\vec{F_E}| = mg

Şimdi Coulomb kuvvetini yazalım:
F_E = k\frac{q q}{x^2} = k\frac{q^2}{x^2} = mg

Şimdi ikinci durumu, yüklerin iki katına çıkarıldığı hali yazalım. Bu durumda da elektriksel kuvvet üstteki topun ağırlığına eşit olmalı çünkü top dengede.
F'_E = k\frac{(2q)(2q)}{x'^2}=k\frac{4q^2}{x'^2} = mg

Artık ilk durumla ikinci durumu eşitleyebiliriz:
F_E = F'_E = mg

k\frac{q^2}{x^2} = k\frac{4q^2}{x'^2}

Düzenleyelim ki x’, kaç x bulabilelim:
\frac{x'^2}{x^2}=\frac{4kq^2}{kq^2} = 4

Yükler iki katına çıkınca aralarındaki mesafe dört katına çıktı, çünkü Coulomb kanunu bir ters kare yasası.

Örnek soru 2: Net elektrik alan

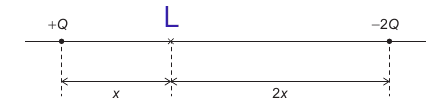
Şekilde aralarında 3x mesafe olacak biçimde noktasal +Q ve -2Q yükleri sabitlenmiştir. +Q yükünden x, -2Q yükünden 2x uzaklıktaki L noktasındaki bileşke elektrik alanın yönü ve büyüklüğü nedir?

Çözüm:

+Q yükü L noktasında sağa doğru (+x yönünde) elektrik alan oluşturur. -2Q yükünün de L noktasında oluşturduğu elektrik alan sağa (+x yönüne) doğrudur. Öyleyse tek yapmamız gereken ayrı ayrı bu elektrik alanların büyüklüklerini hesaplayıp toplamak. Çünkü bir boyutta aynı yöne doğru olan iki vektörden bahsediyoruz.
E_{+Q} = k\frac{+Q}{x^2}

E_{-2Q} = k\frac{2Q}{(2x)^2} = k\frac{2Q}{4x^2} = k\frac{Q}{2x^2}

Eksi işaretini almadık, çünkü -2Q’nun elektrik alanının yönü +x’e doğru. Şimdi toplayalım bunları:
E_{net} = k\frac{Q}{x^2} + k\frac{Q}{2x^2} = \frac{3kQ}{2x^2}

Örnek soru 3: İki artı yükün arasındaki elektrik alanın sıfır olduğu nokta

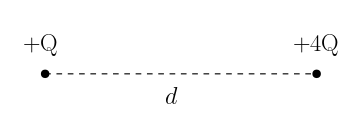
Şekilde aralarındaki mesafe d olan noktasal +Q ve +4Q yükleri sabitlenmiştir. Bu iki yükün net elektrik alanı nerede sıfır olur?

Çözüm:

Soruyu çözmeye atlamadan önce dikkatlice bir bakalım. Elektrik alan hangi bölgelerde sıfır olabilir?

• +Q yükünün solunda olabilir mi? +Q yükünün solunda +Q yükünün elektrik alanı hep sola doğru olur, +4Q yükününkü de sola doğru olur. Yani bu bölgede birbirlerini götürme ihtimalleri hiç yok.
• Peki +4Q yükünün sağında olabilir mi elektrik alan sıfır? Bu da pek mümkün değil, çünkü +4Q yükünün elektrik alanı bu bölgede sola doğru, +Q yükününkü de sola doğru.
• Öyleyse tek seçenek kalıyor, elektrik alan ancak bu iki yükün arasında bir noktada sıfır olabilir. Bu noktanın +Q’dan uzaklığına x diyelim. Bu noktada +Q’nun elektrik alanı sola doğru +4Q’nunki sağa doğru olacak ve büyüklükleri tam birbirine eşit olacak ki, birbirlerini götürecekler. Yani vektör toplamı yapınca sonuç sıfır olacak.

E_{+Q} = E_{+4Q} E_{+Q}=k\frac{Q}{x^2}

+4Q’nun x noktasına uzaklığı (d-x) olmalı öyleyse.
E_{+4Q} = k\frac{4Q}{(d-x)^2}

Şimdi eşitleyelim:
k\frac{Q}{x^2} = k\frac{4Q}{(d-x)^2}

(d-x)^2 = 4x^2

İki tarafın da kare kökünü alalım:
\sqrt{(d-x)^2} = \sqrt{4x^2}

d-x = 2x d = 3x; x = \frac{d}{3}

Örnek soru 4: İki zıt yükün net elektrik alanının sıfır olduğu nokta

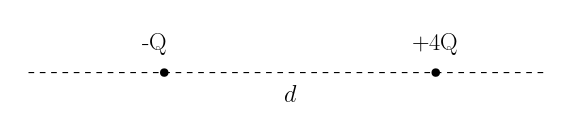
Şekilde aralarındaki mesafe d olan noktasal -Q ve +4Q yükleri sabitlenmiştir. Bu iki yükün net elektrik alanı nerede sıfır olur?

Çözüm:

Ee biz bu soruyu az önce çözmedik mi? Benzer bir soru çözdük ama bu kez zıt yükler var, biri artı biri eksi yüklerin dikkat edin. Yine hemen çözelim diye acele etmeden önce değerlendirelim, nerede sıfır olabilir bileşke elektrik alan?

• -Q yükünün solunda olabilir mi? Olabilir sanki. -Q sağa doğru (+x yönünde) elektrik alan oluşturur, +4Q sola doğru (-x yönünde). Ayrıca -Q’ya daha yakın olacak bu nokta, dolayısıyla -Q’nun elektrik alanı +4Q’nunkini dengeleyebilir.
• +4Q’nun sağında olabilir mi? Olabilir, mi acaba? Önce olur gibi geldiyse, yüklerin büyüklüklerini kıyaslayın. +4Q’ya daha yakın olacak bu nokta ve -Q uzakta kalacak. -Q’nun yükü zaten az, bir de uzakta oldu mu kesinlikle dengeleyemez +Q’nun elektrik alanını.
• Peki iki yükün arasında olabilir mi? Olamaz. Neden olamaz bunu da siz yorum olarak bırakın.

Artık çözebiliriz. -Q’nun solunda x uzaklığında bir nokta için:
E_{-Q} = E_{+4Q}

E_{-Q}=k\frac{Q}{x^2}

+4Q’nun x noktasına uzaklığı (d+x) olmalı bu durumda.
E_{+4Q}=k\frac{4Q}{(d+x)^2}

Artık eşitleyebiliriz:
k\frac{Q}{x^2} = k\frac{4Q}{(d+x)^2}

(d+x)^2 = 4x^2

Eşitliğin iki yanının da kare kökünü alalım:
\sqrt{(d+x)^2} = \sqrt{4x^2}

d+x = 2x x = d

Yani bu iki yükün elektrik alanının sıfır olduğu nokta -Q’nun solunda, yüklerin arasındaki mesafe kadar uzaklıkta. Bu durumda bu nokta +4Q’dan 2d uzaklıkta demektir.

Örnek soru 5: İki boyutta net elektrik alan

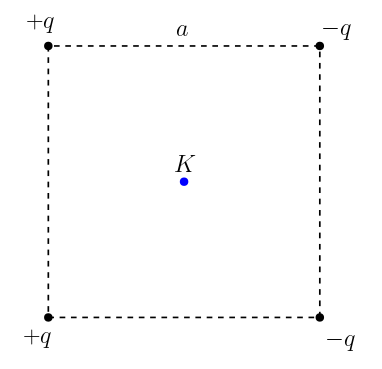
Şekilde gösterilen bir kenarı a uzunluğunda olan karenin köşelerine dört noktasal yük yerleştirilmiştir. Karenin kösegenlerinin kesiştiği K noktasındaki elektrik alanın yönü ve büyüklüğü nedir?

Çözüm:

Öncelikle her yükün oluşturduğu elektrik alanı çizmeliyiz. Aşağıdaki şekilde bu gösteriliyor.

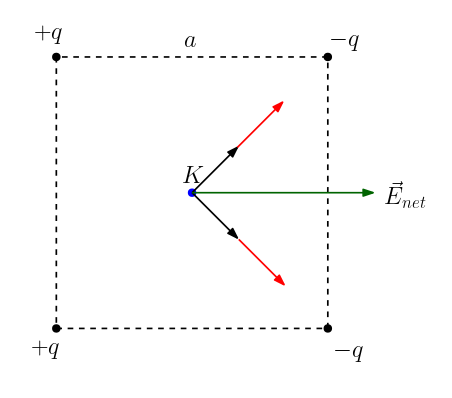
Şekildeki siyah vektörler (oklar) +q yüklerinin elektrik alanlarını, kırmızı vektörler -q yüklerininkileri gösteriyor. +q yüklerinin K noktasına yerleştirilen bir artı yüklü bir test yükünü iteceğini ve -q yüklerinin bu test yükünü çekeceğini hatırlayın. Bu dört vektörü topladığımız zaman yeşille gösterilen net elektrik alan vektörünü elde ediyoruz. Yönü +x’e doğru.

Şimdi de bulduğumuz net elektrik alanın büyüklüğünü hesaplayalım. Bu hesabı vektörleri geometrik olarak toplayarak da yapabiliriz, elektrik alan vektörünü bileşenlerine ayırarak da. Biz geometrik olarak yapalım, çok isterseniz belki bileşenlerine ayırarak yapmayı da başka soruda gösteririz.

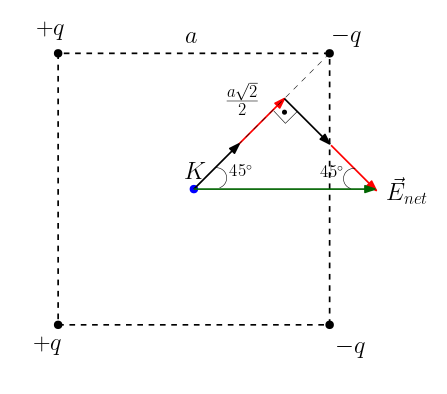
Her yükün K noktasına uzaklığı, karenin köşegeninin uzunluğunun yarısına eşit:
x = \frac{a\sqrt{2}}{2}

Öyleyse her yükün elektrik alanının büyüklüğüne E_q dersek:
E_q = k\frac{q}{(\frac{a\sqrt{2}}{2})^2} = k\frac{q}{(\frac{2a^2}{4})} = k\frac{2q}{a^2}

Demek ki her köşegen boyunca uygulanan elektrik alan bunun iki katı çünkü bir artı (siyah vektör) bir de eksi (kırmızı vektör) yük var. Köşegen boyunca oluşan elektrik alanların büyüklüklerine E_K1 ve E_K2 dersek:
E_{K1} = E_{K2} = 2 \times k\frac{2q}{a^2}= k\frac{4q}{a^2}

E_K1 ve E_K2 ikizkenar bir dik üçgen oluşturuyorlar. Öyleyse net elektrik alanın büyüklüğü de Pisagor bağıntısından bu üçgenin kenarlarının karelerinin toplamının kare köküne eşit.
E^2_{net} = E_{K1}^2 + E_{K2}^2

E_{net} = \sqrt{E_{K1}^2 + E_{K2}^2} E_{net} = \sqrt{(k\frac{4q}{a^2})^2 + (k\frac{4q}{a^2})^2} = \sqrt{2(k\frac{4q}{a^2})^2} = \sqrt{2(\frac{k^2(16q^2)}{a^2})} = 4\sqrt{2}\frac{kq}{a^2}

İlgili Kazanımlar

11.2.1.3. Noktasal yüklerde elektriksel kuvvet ve elektrik alanı ile ilgili hesaplamalar yapar.