Eylemsizlik kuvveti nedir? Asansörde soruları ve çözümleri

Dinamik uygulamalarında şimdi eylemli gözlem çerçevelerinde kuvvet ve harekete ulaştık. Bağıl hız konusunda gözlem çerçevesini öğrenmiştik ve eylemsiz gözlem çerçeveleriyle ilgilenmiştik. Şimdiye kadarki dinamik uygulamaları örneklerinde de eylemsiz gözlem çerçeveleri söz konusuydu.

Şimdi eylemli gözlem çerçevesi ne demek, asansörde ve ivmelenen araçlardaki cisimler nasıl hareket eder sorularına cevap arayacağız. Eylemsizlik kuvveti ya da sanki kuvveti neymiş keşfedeceğiz. Bir asansör örneğiyle başlayalım.

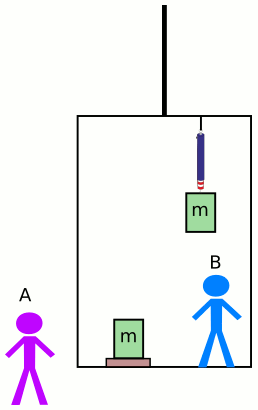
Yukarıdaki resimde bir asansörün içinde özdeş (tıpa tıp aynı) iki cismimiz var ikisinin de kütlesi m. Biri bir dinamometre ile tavana asılmış, diğeri asansörün tabanında bir tartının üstüne yerleştirilmiş. İki de gözlemcimiz var biri asansörün dışındaki Ayşe (A), diğer asansörün içindeki Belgin (B). Şimdi beş farklı durumu değerlendireceğiz. Aslında bir düşünce deneyi yapacağız. Asansörün (1) durduğu, (2) sabit hızla yukarı doğru hareket ettiği, (3) aşağı doğru sabit hızla hareket ettiği, (4) yukarı doğru sabit ivme ile hareket ettiği ve (5) aşağı doğru sabit ivme ile hareket ettiği durumları ele alalım. Her durum için soracağımız sorular da şunlar olacak:

1. Ayşe cisimlerin hareketini nasıl görür? Belgin nasıl görür?
2. Ayşe cisimlerin üzerlerindeki kuvvetleri nasıl görür? Belgin nasıl görür?

Asansör dururken, yukarı ve aşağı doğru sabit hızla hareket ederken ne olur?

1. Asansör dururken Ayşe de Belgin de cisimleri duruyormuş gibi görür. Cisimlerin ivmelenmediğini görürler.
2. Asansör dururken Ayşe de Belgin de hem dinamometre de hem de yerdeki tartıda cisimlerin ağırlığını (mg) okurlar (ölçerler).

Eğer asansör sabit hızla yukarı ya da aşağı hareket ediyorsa, Newton’un birinci kanununa (eylemsizlik) göre hızları (hareket durumları) değişmediği için üzerlerindeki net kuvvet sıfırdır. Bu nedenle Belgin asansörün dışını göremiyorsa hareket edip etmediğini de anlayamaz. Hem Ayşe hem de Belgin eylemsiz gözlem çerçevelerinde oldukları için ikisi için de Newton’un hareket kanunları geçerlidir.

\vec{T} - m\vec{g} = 0 \vec{N} - m\vec{g} = 0

Asansör yukarı doğru ivmelenirken ne olur?

1. Ayşe dışarıdan baktığı için cisimlerin asansörle birlikte yukarı doğru ivmelendiklerini görür. Belgin’e göre ise cisimler hareketsizdir. Belgin de asansöre göre hareketsizdir.
2. Ayşe dışarıdan baktığı için cisimlerin üzerinde net kuvvet olduğunu görür. Çünkü ivmeleniyorlar.

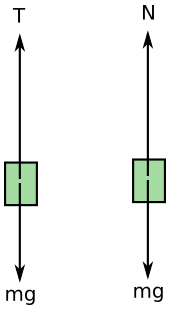
Yukarıdaki resim Ayşe’ye (dışarıdaki eylemsiz gözlem çerçevesine) göre, yukarı yönlü sabit ivmelenen asansörün içinde, tavandaki ve tabandaki cisimlerin serbest cisim diyagramlarını gösteriyor.

Her iki durumda da yukarı yönlü net kuvvet var, ip gerilimi de tepki kuvveti de ağırlıktan daha fazla (T > mg ve N > mg). Bu nedenle Newton’un ikinci kanunu yazarsak:

\vec{F}_{net} = m\vec{a} \vec{F}_{net} = \vec{T} - m\vec{g} \vec{T} - m\vec{g}=m\vec{a}

Ayşe’ye göre tavandaki cismin ivmelenmesini sağlayan dinamometrenin gerilme kuvvetinin ağırlığından büyük olması; tabandaki cisme etkiyen tepki kuvvetinin de ağırlıktan daha büyük olması. Net kuvvet olduğu için ivmeleniyorlar. Eğer dinamometrenin ve tartının hangi değerleri gösterdiğini açıklamak istese işi kolay:

\vec{T} = m\vec{g}+m\vec{a} \vec{N} = m\vec{g}+m\vec{a}

İki cihazın da cismin ağırlığından daha büyük bir değer okuması normal, çünkü ivmelenmeyi sağlayan kuvvet bu cihazlara temaslardan kaynaklanıyor.

Belgin ise cisimlerin ağırlıklarının (yer çekimi ivmesinin) arttığını görür ama kuvvetin sebebini göremez. Çünkü cisimler Belgin’e göre ivmelenmiyorlar, net kuvvet var ama ivmelenmiyorlar. Newton’un birinci kanunu eylemli gözlem çerçevesinde çalışmıyor. Belgin cisimlerin üstünde sanki ağırlığın dışında bir kuvvet daha varmış gibi görüyor. Bu hayali (hayalet) kuvvete sanki kuvveti veya eylemsizlik kuvveti adını veriyor.

Asansör aşağı doğru ivmelenirken ne olur?

1. Ayşe dışarıdan baktığı için cisimlerin asansörle birlikte aşağı doğru ivmelendiklerini görür. Belgin’e göre ise cisimler hareketsizdir. Belgin de asansöre göre hareketsizdir. (Asansörün ivmesinin yer çekimi ivmesinden daha küçük olduğu durumu ele alıyoruz a < g).
2. Ayşe dışarıdan (eylemsiz gözlem çerçevesinden) baktığı için cisimlerin üzerinde net kuvvet olduğunu görür.

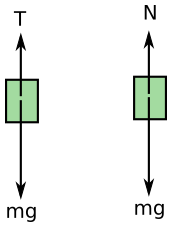
Yukarıdaki resim Ayşe’ye (dışarıdaki eylemsiz gözlem çerçevesine) göre, aşağı yönlü sabit ivmelenen asansörün içinde, tavandaki ve tabandaki cisimlerin serbest cisim diyagramlarını gösteriyor.

Her iki durumda da aşağı yönlü net kuvvet var, ip gerilimi de tepki kuvveti de ağırlıktan daha az (T < mg ve N < mg). Buradan Newton’un ikinci kanunu yazarsak:

\vec{F}_{net} = m\vec{a} \vec{F}_{net} = m\vec{g} -\vec{T} m\vec{g} - \vec{T} =m\vec{a}

Ayşe’ye göre tavandaki cismin ivmelenmesini sağlayan ağırlığının dinamometrenin gerilme kuvvetinden büyük olması bu cisim yere düşüyor. Cismin ağırlığı tabandaki cisme etkiyen tepki kuvvetinden de daha büyük. Net kuvvet olduğu için ivmelenerek hareket ediyorlar. Dinamometrenin ve tartının hangi değerleri gösterdiğini açıklayabilir:

\vec{T} = m\vec{g}-m\vec{a} \vec{N} = m\vec{g}-m\vec{a}

İki ölçüm aracı da cismin ağırlığından daha küçük bir değer okuyor, çünkü ivmelenmeyi sağlayan kuvvet yer çekimi, bu cihazların temasların kuvvetlerinden daha büyük oluyor.

Belgin’e göre ise cisimlerin ağırlıkları (yer çekimi ivmesi) azalıyor, ama neden? Cisimler Belgin’e göre ivmelenmiyorlar (duruyorlar), oysa üstlerinde net kuvvet var gibi görünüyor. Yine Newton’un birinci kanunu eylemli gözlem çerçevesinde geçerli değil, patlıyor. Cisimlerin üstünde sanki ağırlığı azaltan bir başka kuvvet daha varmış gibi görünüyor, işte yine hayali kuvvete sanki kuvveti veya eylemsizlik kuvveti eylemli gözlem çerçevesinde karşımıza çıkıyor.

Yatayda ivmelenen trenin tavanına asılan cisim ve eylemsizlik kuvveti

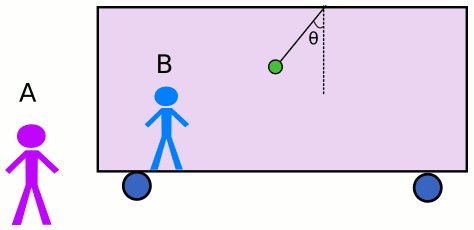
Yukarıdaki şekilde trenin dışındaki eylemsiz gözlem çerçevesinden Ayşe (A) bir trenin sabit ivmeyle +x yönünde (sağa doğru) hareket ettiğini görüyor. Trenin içinde de eylemli gözlem çerçevesinde olan Belgin (B) var. Trenin tavanına bir cisim bir iple asılmış. Hem Ayşe hem de Belgin bu cismin düşeyle bir açı yaptığını görüyorlar. Sorumuz şu: Ayşe’ye ve Belgin’e göre bu cisim neden böyle bir açı yaparak tavanda asılı kalıyor?

Önce Ayşe’nin açıklamasını dinleyelim. Serbest cisim diyagramını kendi gözlem çerçevesine göre şöyle çiziyor:

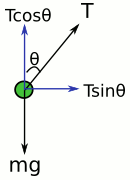
Ayşe’ye göre bu cisim trenle birlikte sağa doğru ivmeleniyor. Düşeyde net kuvvet sıfır olduğu için düşey doğrultuda hareket etmiyor. Ama yatay doğrultuda cismin üstünde net kuvvet var:

\vec{F}_{net} = m\vec{a} \vec{F}_{net} = \vec{T}sin\theta \vec{T}sin\theta = m\vec{a}

Dikkat edin, cisim dengede değil, ivmeleniyor, net kuvvet sıfır değil Tsinθ.

Belgin’in açıklaması da şöyle: Cisim hareket etmiyor, tavanda asılı duruyor. Ama düşeyle açı yapıyor, garip bir durum, sanki üzerinde yatay doğrultuda (-x yönünde) bir kuvvet varmış gibi açı yapıyor, ama kuvveti göremiyorum, sebebini de çıkaramıyorum. Hayalet bir kuvvet bu, eylemsizlik kuvveti. Serbest cisim diyagramını çizecek olsam şöyle olurdu:

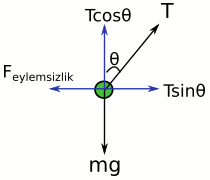
Net kuvvetin sıfır olması lazım çünkü cisim Belgin’e göre ivmelenmiyor. Ama böyle bir kuvvet için aracı yok, nasıl iletilecek bu kuvvet. İşte bu yüzden hayalet kuvvet eylemsizlik kuvveti. Belgin’e göre var, Ayşe’ye göre yok. Newton’un ikinci kanunu da patlıyor, eylemli gözlem çerçevelerinde, çalışmıyor. \vec{F}_{net} \ne m\vec{a}

Örnek soru 1: Asansörde ağırlık ölçümü ve eylemsizlik kuvveti

Aslı bir asansörün içinde, asansör dururken ağırlığını 550 N olarak ölçüyor (g = 10 m/s²). Asansör dışarıdan bakan bir gözlemciye göre:

(a) yukarı doğru sabit 5 m/s² ivme ile hareket ederse tartı kaç N gösterir?

(b) aşağı doğru sabit 5 m/s² ivme ile harket ederse tartıda kaç N okur?

Çözüm:

Yukarıdaki analizimizde asansör yukarı ve aşağı ivmelenirken dışarıdan bakan eylemsiz gözlem çerçevesindeki gözlemciye göre serbest cisim diyagramlarını çizmiştik. Şimdi bunları kullanabiliriz. Tartının gösterdiği kuvvet, tartının Aslı’ya uyguladığı tepki kuvveti (N).

(a) Asansör yukarı doğru ivmelenirken:

\vec{N} = m\vec{g}+m\vec{a} mg = 550 \space N m=\frac{550 \space N}{10\space m/s^2} = 55 \space kg \vec{N} = 550 \space N + 55\times 5 \space kgm/s^2 \vec{N} = 550 \space N + 275 \space N \vec{N} =825 \space N

Aslı ağırlaşmış mı? 🙂

(b) Asansör aşağı doğru ivmelenirken:

\vec{N} = m\vec{g}-m\vec{a} \vec{N} = 550 \space N - 55\times 5 \space kgm/s^2 \vec{N} = 550 \space N - 275 \space N \vec{N} =275 \space N

Şimdi de hafifledi mi?

Örnek soru 2: Trende tavana asılı top ve eylemsizlik kuvveti

Öznur bir trenin içinde tavana astığı bir topun düşeyle 37° açı yaptığını görüyor. Buna göre trenin ivmesinin büyüklüğü kaç m/s²‘dir? (g = 10 m/s², sin 37° = 0,6, cos 37° = 0,8 ).

Çözüm:

Bu durumu da inceledik. Serbest cisim diyagramını çizip rakamları yerleştirmekten başka bir iş kalmadı gibi (siz yapın bunu mutlaka). Şu sonuca ulaşmıştık:

\vec{F}_{net} = m\vec{a} \vec{F}_{net} = \vec{T}sin\theta \vec{T}sin\theta = m\vec{a}

Bir de:

\vec{T}cos\theta = m\vec{g} \vec{T} = \frac{m\vec{g}}{cos\theta}

Bunu bir önceki denklemde yerine koyalım:

\frac{m\vec{g}}{cos\theta}sin\theta = m\vec{a} \vec{a} = \frac{\cancel{m}\vec{g}sin\theta}{\cancel{m}cos\theta} a = 10.\frac{0,6}{0,8} = 7,5 m/s^2

Dinamik ile ilgili mutlaka okumanız gereken yazılar

1. Dinamik nedir? Sürtünmesiz düzlemde sorular ve çözümler
2. Dinamik soruları ve çözümleri
3. Eğik düzlem nedir? Sorular ve çözümler
4. Atwood makinesi nedir? Birbirine bağlı cisimler soruları

Eylemsizlik kuvveti ile ilgili kazanımlar

2017 – 11.1.3.1. Net kuvvetin yönünü belirleyerek büyüklüğünü hesaplar.

• Serbest cisim diyagramları üzerinde cisme etki eden kuvvetlerin gösterilmesi sağlanır.
• Yatay, düşey ve eğik düzlemde sürtünme kuvvetinin yönü belirlenerek büyüklüğünün hesaplanması sağlanır.

2017 – 11.1.3.2. Net kuvvet etkisindeki cismin hareketi ile ilgili hesaplamalar yapar.

• Hesaplamaların günlük hayat örnekleri üzerinden yapılmasına özen gösterilir.
• Sürtünmeli ve sürtünmesiz yüzeyler dikkate alınmalıdır.