Bernoulli ilkesi nedir? Akışkanların basıncı ve akış hızı

Akabilen maddelere akışkan dendiğini, akışkanların aslında sıvılar ve gazları kapsadığını biliyoruz. Basınç kavramında epey ilerledik. Durgun akışkanlarda sıvı basıncını ve gaz basıncını incelemiştik. Bu yazıda hareket eden yani akan akışkanlarda basıncı inceleyeceğiz. Akışkan dinamiği diye sadece akışkanların hareketini inceleyen fiziğin bir alt dalı olduğunu da söylemeliyiz. Akışkanlarda akış hızı ve akışkan basıncı ilişkisini açıklayan süreklilik denklemi ve Bernoulli ilkesi karşımıza çıkacak. Bu ilişkileri anlayabilmemiz için önce akış ile ilgili kavramları gözden geçirmeliyiz. Özellikle akış hızı, debi (hacimsel akış oranı) ve kütlesel akış oranı kavramlarının arasındaki farklar önemli olacak.

Akışkanları eğer boru ya da kanal gibi sınırlayıcı bir şeyin içine koyup incelerseniz, incelediğiniz akış türüne iç akışlar denir. Suyun bir borunun içinde akması iç akıştır. Eğer akışkan böyle fiziksel bir çeperle sınırlanmıyorsa incelenen dış akışlar olur. Arabaların, uçakların ve roketlerin etrafında havanın akması dış akıştır. İç akışlar laminer ya da türbülanslı olabilir.

Laminer akış ve türbülanslı akış nedir?

Akışkanın akışı katmanlar halinde modellenebiliyorsa, akışkanın her parçası düzgün bir doğru boyunca akıyorsa buna laminer akış ya da kararlı akış denir. Laminer akış durumunda akışkanın akış hızı zaman içinde değişmez, sabit kalır. Örneğin, aşağıdaki resimde bir musluktan akan su laminer akış halinde, çünkü suyun akış hızı görece küçük. Suyun nasıl düz bir çizgi halinde aktığına dikkat edin.

Ancak akışkanın içinde bulunduğu kanalın sınır yüzeyleri, akışkanın başka bir cisme temas etmesi ya da akışkanın kendi içindeki sürtünmesi akış hızında düzensiz değişikliklere neden olabilir. Bu düzensiz akışa türbülanslı akış veya girdap akımı denir. Türbülanslı akış çok düzensiz ve karmaşık olabilir. Akışkan dinamiğiyle ilgilenen bilim insanları trübülanslı akışları karmaşık matematiksel denklemler kullanarak modellemeye çalışıyor. Örneğin, aşağıdaki resimde musluktan akan su türbülanslı akış halinde, çünkü suyun hızı yeterince fazla ve bu nedenle akış düz bir çizgi halinde ilerlemiyor, resmin alt kısmında tuhaf şekilde bükülüyor.

Akış çizgisi (akış yolu) ve akış tüpü (akış borusu) nedir?

Akışı incelemek için kullanılan faydalı araçlardan biri akış çizgisi ya da akış yoludur. Akışkanın içinde asılı duran hayali bir parçacığın akış ile birlikte izlediği yola akış yolu ya da akış çizgisi denir. Akışkanın hız vektörü (hızın hem büyüklüğü hem de yönü olduğunu hatırlayın), akış çizgileri daima paraleldir (teğettir). Bunun sonucu olarak akış çizgileri asla kesişmez ve akış çizgilerine dik doğrultuda akış olamaz. (Bunu bir düşünün, ne demek.)

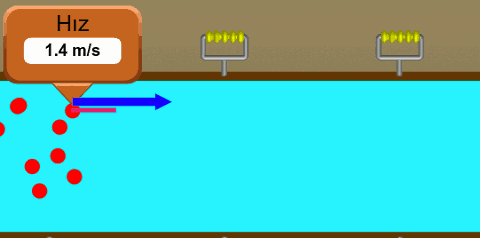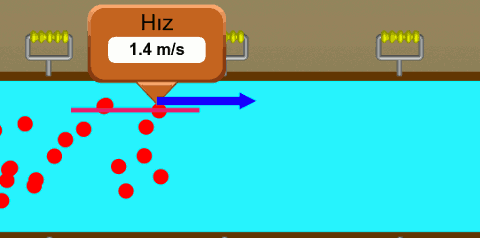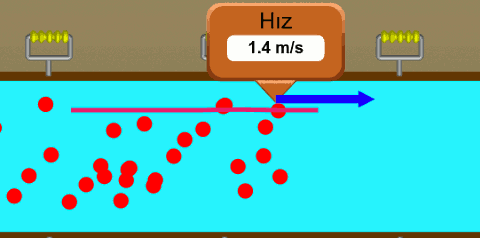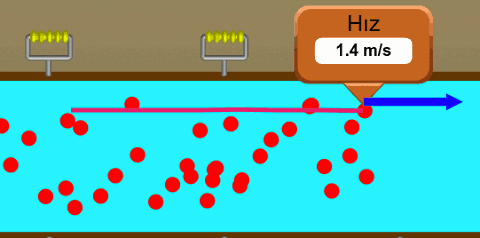
Yukarıdaki resimde bir borunun içinde akan su var. Suyun içinde hayali parçacıkların su ile birlikte hareket ettiğini varsayıyoruz. En üstte ve en öndeki parçacığın hızını ölçüyoruz ve izlediği yolu çiziyoruz (pembe çizgi). İzlediği yol bir doğru, bu laminer bir akış çünkü. Diğer parçacıklar için de aynı şeyi yapsaydık, onların da akış yollarını çizebilirdik. Şöyle görünürdü:

Akış çizgilerinin etrafına çizdiğimiz hayali tüpe ya da boruya da akış tüpü ya da akış borusu denir. Yukarıdaki akış tüpü doğrusal akış çizgilerini temsil ettiği için kesit alanı A olan bir silindir şeklinde.

Akış çizgileri doğrusal olmak zorunda değildir. Örneğin, aşağıdaki resimde daralan bir boruda akan su için, suyla birlikte hareket eden yan yana dizilmiş hayali parçacıklar gösteriliyor. Bu parçacıklar için akış çizgilerini ve akış tüpünü çizebilir misiniz?

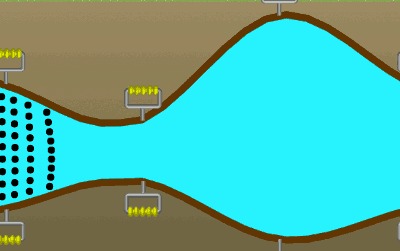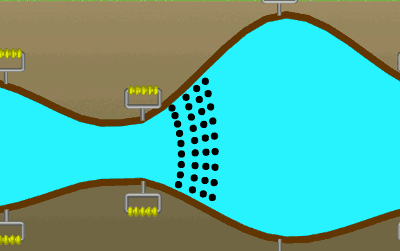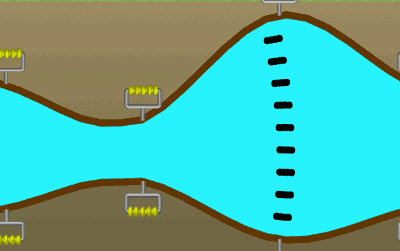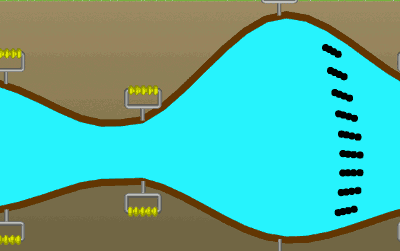
Akış hızı ve debi (hacimsel akış oranı) nedir?

Öncelikle hızın ne olduğunu hatırlayalım: birim zamandaki yer değiştirme. Yer değiştirme vektörel bir büyüklük olduğu için hız da vektördür. Akış hızı akışkanın birim zamandaki yer değiştirmesidir, dolayısıyla vektörel bir büyüklüktür, birimi hız birimidir yani m/s’dir. Akış hızı akışın farklı bölgelerinde değişebilir.

Debi veya hacimsel akış oranı, akış tüpünün herhangi bir kesitinden birim zamanda (yani bir saniyede) geçen hacim miktarıdır. Hacim skaler bir büyüklük olduğu için debi de skalerdir, birimi L/s (litre bölü saniye) ya da m³/s olarak verilebilir. Debinin formülü (matematiksel modeli) şöyledir:

Debi = \frac{\Delta V}{\Delta t}

Debiye bazı kitaplarda hacimsel akış hızı deniyor, kavram yanılgısına yol açabilir bu adlandırma. Hız çok özel bir terim, sadece yer değiştirmenin geçen zamana oranı olarak tanımlıyoruz. Bu nedenle herhangi bir büyüklüğün zamana oranını hız olarak tanımlamak pek uygun değil. Oran demek daha tutarlı.

Son olarak da kütlesel akış oranı tanımlayabiliriz. Debi hacmin geçen zamana oranıydı, benzer biçimde kütlesel akış oranı da bir akış tüpünden birim zamanda geçen sıvının kütlesine denir. Kütle skaler olduğu için bu da skaler bir büyüklüktür, birimi de kg/s’dir. Kütlesel akış oranına tıpkı debi de olduğu gibi bazı kitaplar kütlesel akış hızı diyor, kesinlikle hız değil bu, oran. Kütlesel akış oranının formülü de:

Kutlesel \space akis \space orani = \frac{\Delta m}{\Delta t}

Süreklilik denklemi nedir?

Gazlar sıkıştırılabilir, ama sıvılar sıkıştırılamaz olarak kabul edilir (çünkü belli şartlar altında çok az sıkıştırılabilirler.) Süreklilik denklemi, bir borunun içinde hareket eden sıkıştırılamaz akışkanlarda (yani sıvılarda), borunun içindeki her noktada akışkanın akış hızı ile borunun kesit alanının çarpımının eşit olduğunu söyler.

Borunun kalınlığı aynı olsa süreklilik denklemi pek önemli olmayabilirdi, ama borunun kalınlığının (yani kesit alanının) değiştiği durumlarda akışkanın hızını bulmamızı sağlar. Süreklilik denkleminin formülü şöyledir: (A kesit alanı, v akış hızını gösteriyor.) A₁v₁ = A₂v₂

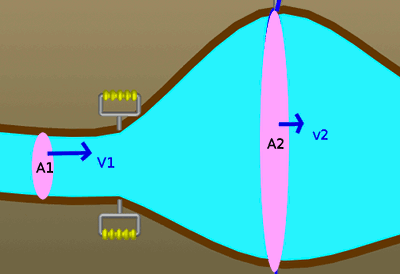
Yukarıdaki resimde borunun kesit alanı ince olan bölgesinde akışkanın hızının, borunun geniş olan bölgesine göre daha fazla olduğu görülüyor.

Aşağıdaki resim simülasyonda bunu daha belirgin olarak sunuyor.

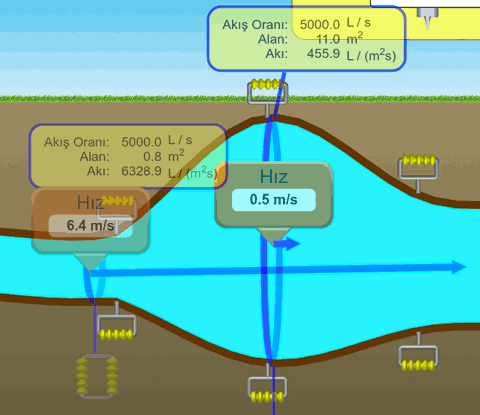
Resimde borunun dar bölgesinin kesit alanı 0,8 m², bu noktadaki akış hızı 6,4 m/s. Borunun geniş noktasındaki kesit alan 11 m², akış hızı da 0,5 m/s. Kesit alan azalınca akış hızının arttığını, kesit alan artınca akış hızının azaldığını görüyoruz. (Bu arada simülasyondan aldığımız kesit alan ve akış hızı verilerinin çarpımları tam eşit olmuyor, bu neden olabilir?)

Süreklilik denkleminin doğru olduğuna neden inanalım? Mantık yürütüp delil bulabilirsek inanmak için güçlü sebeplerimiz olur. Bir borunun içinde su dışarı sızmıyorsa, boruya birim zamanda giren ve çıkan su miktarı aynı olmak zorundadır. Çünkü borunun sadece bir tarafından su ekleniyor, başka bir yerden su girmiyor. Borunun içinde kendiliğinden yeni su oluşamayacağına göre, su miktarı korunur. Bir saniyede borunun ucundan m kütleli su girdiyse, borunun her yerinden bir saniyede m kadar suyun geçmesi gerekir. Bu sıvı sıkıştırılamayacağı için birim zamanda borunun her yerinden geçen hacmin de sabit olmasını gerektirir. Yani debi (hacimsel akış oranı) borunun içinde her noktada sabit olmak zorundadır. (Su miktarının sabit olması en çok kafa karıştıran noktalardan biri, iyice bir düşünmelisiniz bunu.)

\frac{\Delta V_1}{\Delta t_1} = \frac{\Delta V_2}{\Delta t_2}

Hacmi kesit alan çarpı yer değiştirme olarak tanımlayabiliriz. V’nin büyük harfle yazıldığına ve hacmi temsil ettiğine dikkat edin. Bu durumda:
\Delta V = A \Delta x
A_1\frac{\Delta x_1}{\Delta t} = A_2\frac{\Delta x_2}{\Delta t}
v = \frac{\Delta x}{\Delta t}
A_1 v_1 = A_2 v_2
v’nin küçük harfle yazıldığına ve akış hızını temsil ettiğine dikkat edin.

Bernoulli ilkesi (prensibi) nedir? Akış hızı ile basınç ilişkisi nasıldır?

Buraya kadar hep akışkanın hızından bahsettik, şimdi basınca geldik. Bernoulli ilkesi (prensibi ya da denklemi), ideal, sıkıştırılamaz, laminer akış halinde olan akışkanlarda, akış hızı ile basıncın ilişkisini açıklar. Akışkanının basıncı dediğimizde akışkanın akmasını engelleyen cisimlere uygulayacağı basıncı değil, akışkanın içinde bulunduğu sistemin çeperine yaptığı basıncı kastediyoruz. İsviçreli fizikçi Daniel Bernoulli 1738 yılında bu denklemi keşfettiği için onun adıyla anılıyor.

Aşağıdaki resimlerde, (simülasyonu kullanarak) bir borunun içinde akan suyun hızı ve akan suyun borunun üst çeperine uyguladığı basınç ölçülüyor.

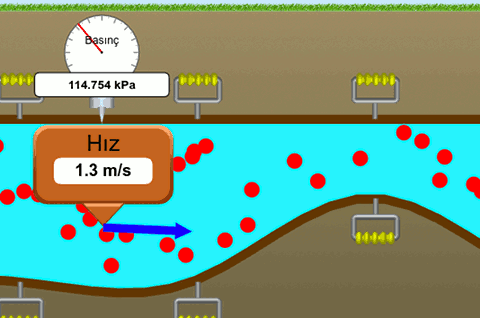
Bu resimde borunun geniş olan kısmında hızın 1,3 m/s, basıncın 114, 75 kPa olduğunu görüyoruz.

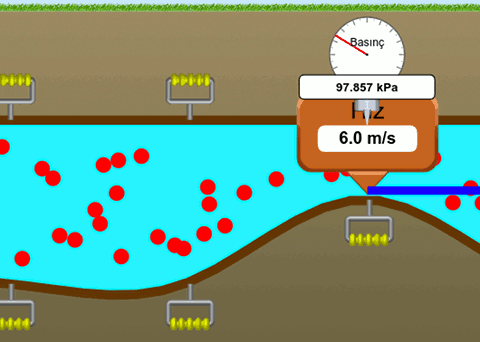
Bu resimde ise borunun dar olan kısmında ise hızın 6 m/s basıncın da 97,86 kPa olduğunu görüyoruz.

Basıncı aynı yükseklikte, yani borunun üst çeperinde ölçtüğümüze dikkat edin. Akışın yatayda olmasını sağlıyoruz. Bu gözlemlerden varacağımız sonuç Bernoulli prensibinin ilk sonucu olacak: Akışkanın hızı artarsa uyguladığı basınç azalır. Bir başka deyişle akışkan hızı ile basınç ters orantılıdır. (Bu sezginize ters gelmiyor mu? Hızlandıkça basıncın artmasını beklemez miydiniz?)

Şimdi de Bernoulli ilkesinin ikinci kısmını açıklayalım. Yine simülasyonda ölçüm yapıp karşılaştıracağız. Bu kez basıncı farklı derinliklerde ölçeceğiz. Unutmamamız gereken sıvının bu kez hareket ediyor olması, durgun sıvılardan bahsetmiyoruz.

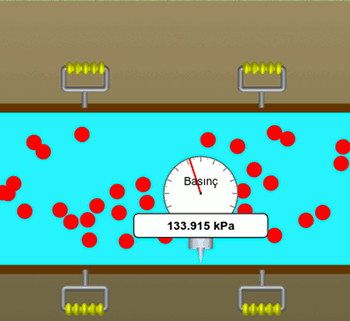
Yukarıdaki resimde borunun alt çeperine uygulanan, yani derin yerdeki basıncın 133, 9 kPa olduğunu görüyoruz. Akış hızı sabit olduğu için onu ölçmedik.

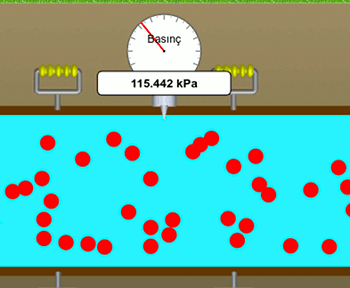
Bu resimde de borunun üst çeperine uygulanan yani daha sığ yerdeki basıncın daha az olduğunu görüyoruz. Tıpkı durgun sıvılarda olduğu gibi, akan akışkanlarda da sıvı basıncı derinlikle doğru orantılı, derinlik arttıkça basınç artıyor.

Son olarak Bernoulli ilkesi denkleminin enerjinin korunumundan kaynaklandığını söylemeliyiz. Kazanımlar Bernoulli denklemi verilmez diyor, siz de ezberlemeyin ama denklem neye benziyormuş bir görün. Bernoulli prensibinin formülü şöyle:
P_1 + dh_1 + \frac{1}{2}dv_1^2 = P_2 + dh_2 + \frac{1}{2}dv_2^2
P basıncı, h yüksekliği (derinliğin tersini), d akışkanın özkütlesini, v akış hızını gösteriyor.

Akış hızı ve akışkan basıncı ile ilgili Günlük Hayat Örnekleri

• Rüzgar tünelleri otomobil, uçak, gemi, roket ve uzay mekiği gibi araçların en verimli şekilde tasarlanması için kullanılır.
• Uçakların kanatları ve teknelerin yelkenleri havanın akış hızını değiştirip basıncı düşürerek kaldırma ya da emme kuvveti oluşması için tasarlanır.
• Bir bahçe hortumunun ağzını baş parmağınızla sıkıştırırsanız, kesit alanı daralttığınız için suyun daha hızlı akmasını sağlarsınız. Fıskiyeler böyle çalışır.
• Musluktan akan suyun yere yaklaştıkça incelmesi, suyun yere yakın bölgelerde daha hızlı akmasına neden olur.
• Fırtınalarda çok hızlı esen rüzgar, çatıların üstündeki basıncı düşürüp havanın emme kuvveti uygulamasına ve çatıların uçmasına neden olabilir.
• Süreklilik denklemi, Bernoulli ilkesi ya da akışkan hızı ve akışkan basıncının kılcallıkla bir ilgisi yoktur. (Niye yazdım, çünkü böyle düşünenler var öğrenciler arasında.)

Akış hızı ve akışkan basıncı ile ilgili kazanımlar

2017 – 10.2.1.2. Akışkanlarda akış sürati ile akışkan basıncı arasında ilişki kurar.

• Bernoulli ilkesi’nin günlük hayattaki örnekler (çatıların uçması, şemsiyenin ters çevrilmesi, rüzgârlı havalarda kapıların sert kapanması gibi) üzerinden açıklanması sağlanır.
• Bernoulli ilkesi’yle ilgili matematiksel hesaplamalara girilmez.
• Deneyler veya simülasyonlardan yararlanılarak kesit alanı, basınç ve akışkan sürati arasında bağlantı kurulması sağlanır.
• Günlük hayatta akışkan basıncının sağlayabileceği kolaylıklar (uçakların uçması gibi) ve olumsuz etkilerine karşı alınması gereken sağlık ve güvenlik tedbirleri (yüksek süratle hareket eden araçlara yaklaşılmaması gibi) vurgulanır.
• Tansiyonun damarlardaki kan basıncı olduğu vurgulanarak öğrencilerin tansiyon aletinin çalışma prensibini araştırmaları sağlanır.

Akış hızı ve akışkan basıncı ile ilgili simülasyon

Akışkan basıncı ve akış PHET simülasyonu süreklilik denklemi ve Bernoulli ilkesini anlamakta kullanabileceğiniz değerli bir araç.

Kaynaklar

Streamlines and Stream Tubes

NASA akışla ilgili açıklamalar