Kütle çekim kuvveti nedir? Örnek sorular ve çözümleri

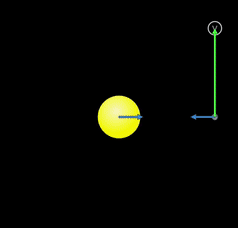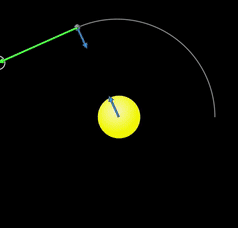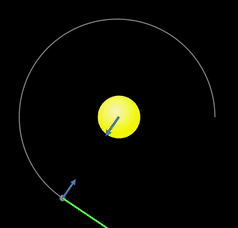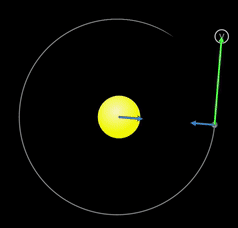
Çembersel hareketi anladıktan sonra gezegenlerin Güneş etrafındaki hareketiyle ilgili çok önemli bir soru karşımıza çıkıyor. Eğer gezegenler çembersel hareket yapıyorlarsa onların yörüngede kalmalarını sağlayan merkezcil ivmenin kaynağı olan kuvvet ne? Bir çekim kuvveti olmalı ki buna kütle çekim kuvveti diyoruz. Ama doğadaki dört temel kuvvetten en gizemlisi hakkında daha derine girmeden önce soruyu bir daha düşünelim. Aşağıdaki animasyonda bir yıldızın etrafında dönen bir gezegenin üzerindeki kütle çekim kuvveti aniden kaldırılıyor. Yeşil ok gezegenin hız vektörünü gösteriyor. Üzerinde net kuvvet olmayan cisim Newton’un birinci hareket kanununa göre hareket durumunu koruyor, yani hız vektörü sabit kalıyor, artık dönmüyor. Şimdi dönmenin sebebi olan kütle çekimini incelemeye hazırız.

 

Aynı animasyonu bir de kuvvetler varken izleyelim. Aşağıdaki animasyonda mavi oklar kuvvetleri gösteriyor. Neden kuvvet demedik de çoğul konuştuk, kuvvetler dedik? Newton’un üçüncü hareket yasası olan etki tepkiyi hatırlayın. Kuvvetler daima çiftler halinde gelir. Gezegenlerin ayları, yıldızların gezegenleri ve yapay uydular kütle çekim kuvveti sayesinde yörüngede kalırlar.

 

Newton’un Evrensel Kütle Çekim Yasası

Artık kütle çekim kuvvetini tanımlayabiliriz. Modern bilimin öncüsü Newton hareketi anlamamızı sağladığı gibi kütle çekimini de anlamamızı sağlamış. Fikri şu: kütle diye maddenin bir özelliği var, iki kütle birbirini daima çeker. Neden çeker, çünkü doğa böyle işliyor diyebiliriz. Nasıl çeker işte kütle çekim kuvvetinin matematiksel modeli ya da formülü tam olarak bunu tanımlıyor. Aşağıdaki resimde iki kütle, aralarındaki mesafe ve uygulanan kuvvetler gösteriliyor.

\vec{F_{21}} = -\vec{F_{12}}

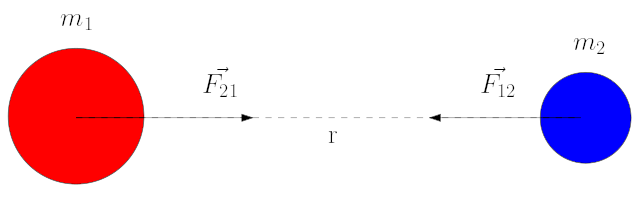
Yani kütlelerin birbirine uyguladıkları kuvvetler eşit ve zıt yönlü.
|\vec{F_{21}}| = |\vec{F_{12}}| = |\vec{F}|

Yani kuvvetlerin büyüklükleri eşit.
|\vec{F}| = G \frac{m_1 m_2}{r^2}

Yani bir kütlenin diğerine uyguladığı kuvvet kütlelerin çarpımıyla doğru, kütlelerin arasındaki uzaklığın karesiyle ters orantılı. Aradaki mesafeyi kütlelerin merkezleri arasındaki mesafe olarak aldığımıza dikkat edin. G de evrensel çekim sabiti, yani sadece kuvveti ölçeklendirmeye yarıyor ve oldukça küçük bir değeri var. Tam olarak:

G = 6,67 × 10^-11 Nm²/kg²

Ters kare kanunları

Newton’un evrensel kütle çekim yasasının biçimi daha önce gördüğünüz başka bir yasaya benziyor mu? Elektriksel kuvveti hatırlayın. Coulumb kanununda iki yük birbirine tıpkı kütle çekim gibi kuvvet uyguluyordu:
\vec{F_E} = k\frac{q_1 q_2}{r^2}

Ters kare kanunu demek aralarındaki mesafenin karesiyle ters orantılı demek. Dikkat edin elektrostatik kuvvet ile kütle çekimi çok benziyor. Ama önemli iki fark var. İlk fark kuvvetin çekme ve itme olarak ortaya çıkmasında. Elektriksel kuvvet çekme ya da itme şeklinde olabiliyor. İki yük aynı işaretliyse itiyor, zıt işaretliyse çekiyor. Kütle çekimde ise sadece çekme var, itme yok. Çünkü maddenin elektrik yükü özelliğinde iki çeşit var, kütle özelliğinde ise sadece bir çeşit, eksi kütle diye birşey yok. İkinci fark da sabitlerin değerlerinde k çok büyük bir sayıyken G çok küçük bir sayı.

Şimdi bir kaç örnek çözüp kütle çekim kuvvetini içselleştirmeye çalışalım.

Örnek soru 1

Kütlesi 420 ton olan Uluslararası Uzay İstasyonu’nun yörüngesi yeryüzünden 300 km yüksekte ise, Dünya’nın istasyona uyguladığı kütle çekim kuvveti kaç Newton’dur? (Dünya’nın kütlesini 6 x 10²⁴ kg yarıçapını 6000 km alınız.)

Çözüm

Bu soru sadece formülde bildiklerimizi yerine koyarak çözebileceğimiz bir soru. Birimlere dikkat etmemiz lazım kütleyi kg, uzaklığı m cinsinden yazmalıyız.
F = \frac{(6,67 \times 10^{-11})(6 \times 10^{24})(4,2 \times 10^5)}{((6000 + 300) \times 10^3)^2} = 4,23 \times 10^{6} N

Yeryüzündeki kütle çekim kuvvetiyle kıyaslayalım:
F = \frac{(6,67 \times 10^{-11})(6 \times 10^{24})(4,2 \times 10^5)}{((6000) \times 10^3)^2} = 4,67 \times 10^{6} N

Yani yörüngedeki kütle çekimi kuvveti yer yüzündekinin yaklaşık %90’ı kadar (4,23/4,67 = 0,9). Yerçekimsiz ortam derken kütle çekimi kuvvetinin olmadığı anlamına gelmediğini görmüş olduk.

Örnek soru 2

Kütleleri 100 kg olan iki kişi aralarında 1 cm mesafe olduğunda birbirine kaç Newton kütle çekim kuvveti uygular?

Çözüm

Neden yerçekimi demiyoruz da kütle çekim diyoruz. Çünkü kütlesi olan herşey kütlesi olan başka şeyleri çeker. Şimdi bu iki kişinin birbirine kütleleri olduğu için uyguladıkları kuvveti bulalım.
F = \frac{(6,67 \times 10^{-11})(100)(100)}{(1 \times 10^{-2})^2} = 6,67 \times 10^{-11} N

Bir Newton’un on milyarda biri kadar. O kadar küçük ki bu kuvvet hissetmemiz mümkün değil. Bu nedenle kütle çekimi kütlesi çok büyük olan galaksiler, yıldızlar ve gezegenler gibi gök cisimlerinde baskın hale geliyor.

Newton’un kütle çekim yasası doğru mu?

Newton’un kütle çekim açıklaması yüzyıllarca doğru olarak kabul edildi. Ama Newton’un bile içine sinmeyen sorunlar vardı. En önemlilerinden biri nasıl oluyordu da bir kütle uzaktan diğer kütleyi etkileyebiliyordu. Arada bu iletimi sağlayan bir mekanizma, taşıyıcı paçacıklar gibi birşey yoktu. Daha sonra tıpkı elektrik alan fikrinde olduğu gibi kütle çekim alanı fikri yaygınlaştı. Yani kütle çekim uzayın bir özelliğiydi ve kütlesi olan cisimler uzayın bu özelliğini değiştiriyordu, böylece alan kuvveti iletiyordu. Ama sorunlar bitmedi, Newton’un kütle çekim yasasının tahminleriyle örtüşmeyen gözlemler yapıldı. Biriken huzursuzluğu sonunda Einstein çözdü. Einstein’a göre kütle çekim kuvveti diye birşey yoktu. Kütle uzay-zamanı büküyordu. Cisimler bükülen uzay-zaman üzerindeki en kısa yollarda hareket ediyorlardı. Bu da bize bir kuvvet uygulanıyor izlenimi veriyordu.

Şu anda Einstein’ın genel görelilik kuramı kütle çekimin en iyi açıklaması olarak kabul ediliyor. Şimdiye kadar yapılan gözlemler Einstein’ın kuramının tahminleriyle çok iyi uyuşuyor. Ama fiziğin iki kuramı olan kuantum ile genel görelilik başarılı bir şekilde birleştirilebilmiş değil, kuantum kütle çekim nasıl çalışıyor bilmiyoruz. Tüm maddeyi açıklayan Standart model’de kütle çekimi yok. Graviton adı verilen taşıyıcı parçacıklar kuramsal olarak öne sürülüyor ama varsa bile bunların ölçülmesi neredeyse imkansız.

Peki Newton yanlış mı anladı kütle çekimini? Öyleyse neden doğrusunu öğretmiyoruz lisede ve üniversitede? Yanlış demiyoruz, belli sınırlar dahilinde güvenilir yanıtlar veren modeller diyoruz. Newton’un evrensel çekim yasası da böyle bir model. Uyduları yörüngeye oturturken hala Newton’un yasasını kullanıyoruz, çünkü yeterince büyük ve yavaş sistemleri gayet iyi açıklıyor. İşte bilimin gizemi ve harikalığı burada. Doğanın nasıl çalıştığını anlamaya çalışıyoruz, bazen çok yaklaştığımızı hissediyoruz, ama asla doğa tam olarak kesinlikle böyledir diyemiyoruz. Bu ifadeyi yanlış anlamayın, bilim elimizdeki en iyi bilgi üretme yöntemi ve teknoloji meyvesinin de keyfini sürüyoruz.

Kütle çekim kuvvetiyle ilgili kazanımlar

12.1.4.1. Kütle çekim kuvvetini açıklar.

• Kütle çekim kuvvetine değinilir. Matematiksel model verilir. Matematiksel hesaplamalara girilmez.
• Yapay uydular, ay ve gezegenlerin hareketleri açıklanır. Matematiksel hesaplamalara girilmez.