Sıvı basıncı hangi değişkenlere bağlıdır? Simülasyon deneyleri

Daha önceki yazımızda sıvı basıncının bağlı olduğu değişkenleri ve sıvı basıncının formülünü anlatmıştık. Şimdi Basınç Altında PHET simülasyonunu kullanarak bu değişkenlerin sıvı basıncını nasıl etkilediğini inceleyeceğiz. Formülü çıkaracağız demek isterdim, ama formülü zaten biliyorsanız deneysel olarak sağlamasını yapacağız. Sırasıyla şu değişkenlerin sıvı basıncını nasıl etkilediğini inceleyeceğiz.

1. Atmosferin olup olmaması
2. Sıvının derinliği
3. Sıvının özkütlesi
4. Sıvının bulunduğu yerdeki yerçekimi ivmesi (kütle çekim alanının büyüklüğü)

Elimizde dört farklı değişken olduğu için dikkatli hareket etmemiz lazım. Her seferinde yalnızca bir değişkeni değiştirip (bizim değiştirdiğimiz değişkene bağımsız değişken diyoruz), diğer değişkenleri sabit tutmalıyız ki, sadece bağımsız değişkenin bağımlı değişkenin (sıvı basıncının) üzerindeki etkisini görebilelim. Dört değişkenimiz var, demek ki dört kontrollü deney yapmamız lazım. Kontrollü deney demek kontrol değişkenlerini (bağımısız değişkenin dışındaki tüm değişkenleri) sabit tutmak demek. Öyleyse başlayalım.

Deney 1: Atmosfer Sıvı Basıncını nasıl etkiler?

Araştırma sorumuz başlıkta yazılmış. Atmosferin olup olmamasına göre sıvı basıncı değişir mi? Soruyu böyle yazarsak, hipoteze, yani sınayabileceğimiz bir önermeye çevirmemiz de kolay. Hipotezimizi şöyle ifade edebiliriz öyleyse:

• Atmosferin varlığı sıvının basıncını değiştirmez.

İstersek hipotezimizi olumlu biçimde de yazabilirdik:

• Atmosferin olması sıvı basıncını değiştirir.

Hatta atmosferin varlığının sıvı basıncını artırıp azaltmasıyla ilgili hipotezler de kurabilirdik:

• Atmosferin olması sıvı basıncını artırır.
• Atmosferin olması sıvı basıncını azaltır.

Deneyimizin amacı bu önermeleri (hipotezleri) test etmek. Doğru mu yanlış mı bulmaya çalışmak.

Deneyin Tasarımı

Simülasyon bize atmosferin varlığını kontrol etme şansı veriyor. Gerçekte yapamayabilirdik, ama simülasyonda yapabiliyoruz. Öyleyse tek yapmamız gereken atmosferi var veya yok durumuna getirmek.

Bağımlı değişken: Biz hangi değişken de değişiklik olmasını açıklamak istiyoruz? Sıvı basıncı öyle değil mi? Nasıl ölçeceğiz sıvı basıncını? Simülasyon bir barometre sağlıyor, onu kullanacağız.

Bağımsız değişken: Bağımlı değişkendeki değişime sebep olmasını beklediğimiz değişken bu. Bu durumda atmosferin varlığı. Nasıl değiştireceğiz bağımsız değişkenimizi? Zaten iki değer alabiliyor, var veya yok. Simülasyon bir radyo düğmesiyle bunu yapabilmemize olanak sağlıyor.

Kontrol değişkenleri:

1. Sıvının derinliği. Sıvının basıncını hep aynı derinlikte ölçmeliyiz. Çünkü eğer derinlik basıncı etkiliyorsa ve biz atmosfer varken sıvının basıncını belli bir derinlikte atmosfer yokken başka bir derinlikte ölçersek, o zaman atmosferin etkisinin dışında derinliğin etkisini de karıştırmış oluruz. Ölçümlerimiz arasındaki ilişkinin atmosferin varlığından mı sıvının derinliğinden mi kaynaklandığını ayırt edemeyiz. Zaten kontrol değişkeni demek, bir değişkeni sabit tutarak o değişkenin bağımlı değişken üzerindeki etkisini kontrol etmek demek.
2. Sıvının özkütlesi (yoğunluğu): Sıvının basıncını ölçerken hep aynı tür sıvıyı kullanmalıyız, yoksa ölçümlerimiz özkütle farkından etkilenebilir. Derinlikle ilgili argümanımızın aynısı yani.
3. Yerçekimi ivmesi: Yerçekimi ivmesini de sabit tutmalıyız. Bu tuhaf gelebilir, yani zaten Dünya’da yapıyoruz deneyi diye düşünebilirsiniz. Ama simülasyon bize hayal etme özgürlüğü sağlıyor. Yerçekimi ivmesini istediğimiz gibi değiştirebiliyoruz. Ama bu deney için değiştirmemeliyiz, sabit tutmalıyız.
4. Sıvının bulunduğu kabın şekli değişkenini de sabit tutmalıyız.

Deneyin İşlem Basamakları

Aşağıdaki resimde veri almamız için gereken koşul görülüyor.

 

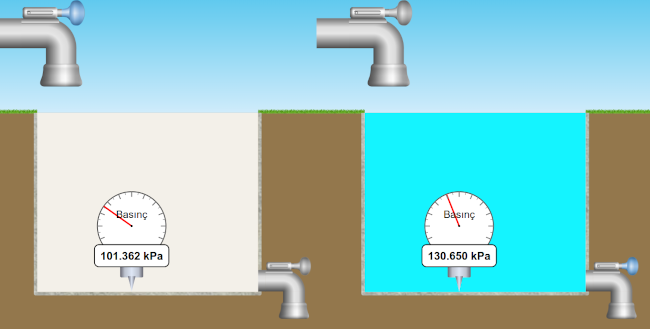
1. Önce, havuzun sağ altındaki musluğu kullanarak havuzu boşaltalım.
2. Sonra boş havuzun tabanındaki basıncı ölçecek şekilde barometreyi yerleştirelim. Boş havuzda atmosfer varken barometrenin gösterdiği basınç değerini okuyalım ve kaydedelim.
3. Sonra sol üstteki musluğu kullanarak havuzun içine derinlik 3 metre olana kadar su dolduralım. Bu durumdaki barometrenin gösterdiği basınç değerini okuyalım ve kaydedelim.
4. Sıvı yokken ve sıvı varken ölçtüğümüz basınçların farkını hesaplayalım ve kaydedelim.
5. Şimdi atmosfer yok radyo düğmesini tıklayalım. Simülasyonun arkaplanının siyaha dönmüş olmasını görelim.
6. İlk dört basamağı atmosferin olmadığı durum için tekrar edelim.

Veri Toplama

Aşağıda topladığımız veriler görünüyor. Siz de başka derinlikleri kullanarak kendi verinizi toplayabilirsiniz. kPa kiloPascal demek, yani 1000 Pascal.

Atmosfer	Sıvı Yokken Basınç (kPa)	Sıvı Varken Basınç (kPa)	Basınç Farkı (kPa)
Var	101,361	130,405	29,044
Yok	0	29,080	29,080

Veri Analizi

Atmosferin var olduğu durumdaki basınç farkını neden hesapladık? Çünkü atmosfer varken, sıvı olmadığı halde bir basınç zaten var. Buna açık hava basıncı diyoruz. Demek ki iki durum (yani atmosferin olması veya olmaması) arasında kıyaslamamız gereken değerler basınç farkları.

Sonuç ve Değerlendirme

Atmosfer varken de yokken de sıvı basıncını 29 kPa bulduk. Demek ki, atmosferin varlığı sıvı basıncını etkilemiyor sonucuna varabiliriz. Peki neden tam olarak aynı değerler çıkmadı, birinde 29,044 kPa diğerinde 29,080 kPa çıktı? Cevaplarınızı yorumlarda bekliyorum.

Hipotezimiz “atmosferin varlığı sıvı basıncını değiştirir” şeklindeydi. Bu hipotezi yanlışladık. Yani atmosfer basıncı sıvının basıncını değiştirmez sonucuna ulaştık.

Deneyin videosu

Deney 2: Sıvının Derinliği Sıvı Basıncını nasıl etkiler?

Şu araştırma sorularından birine cevap arıyoruz:

1. Sıvının derinliği ile sıvının basıncı arasındaki ilişki nasıldır?
2. Sıvının basıncı sıvının derinliği göre nasıl değişir?

Hipotezimiz şöyle olabilir:

• Sıvının derinliği sıvının basıncıyla doğru orantılıdır. Derinlik arttıkça basınç da artar.

Deneyin Tasarımı

Simülasyon bize sıvının derinliğini kontrol etme olanağı sağlıyor. Öyleyse değişkenlerimizi belirleyelim:

Bağımlı değişkenimiz yine sıvı basıncı ve barometreyle ölçeceğiz.

Bağımsız değişkenimiz sıvının derinliği, simülasyon bize bir cetvel sağlıyor, derinliği bu cetveli kullanarak ölçeceğiz.

Kontrol değişkenleri: Sıvının özkütlesini, yerçekimi ivmesini, ve sıvının bulunduğu kabın şeklini sabit tutacağız. Atmosferin etkisinin olmadığını öğrendiğimiz için onu kontrol etsek de olur etmesek de. Ama atmosfersiz ortamda doğrudan sıvının basıncını okuyabildiğimizi öğrendik bir önceki deneyden. Bu nedenle atmosfersiz ortamda yapalım deneyi. Atmosferli ortamda da yapabilirsiniz, ama bu kez basınç farklarını hesaplamanız gerekir.

Deneyin İşlem Basamakları

1. Önce havuzun tamamını sıvıyla dolduralım.
2. Sonra cetveli yerleştirelim ve çizgileri göster seçeneğini seçelim. Böylece sıvının derinliğini daha net göreceğiz.
3. Havuzun üst yüzeyinde, yani yer seviyesinde basıncı ölçelim ve ölçümümüzü kaydedelim.
4. 0m – 3 m aralıkları için, derinliği her seferinde 0,2 m (20 cm) artırarak, basınç ve derinlik ölçümlerimizi tekrarlayalım ve kaydedelim.

 

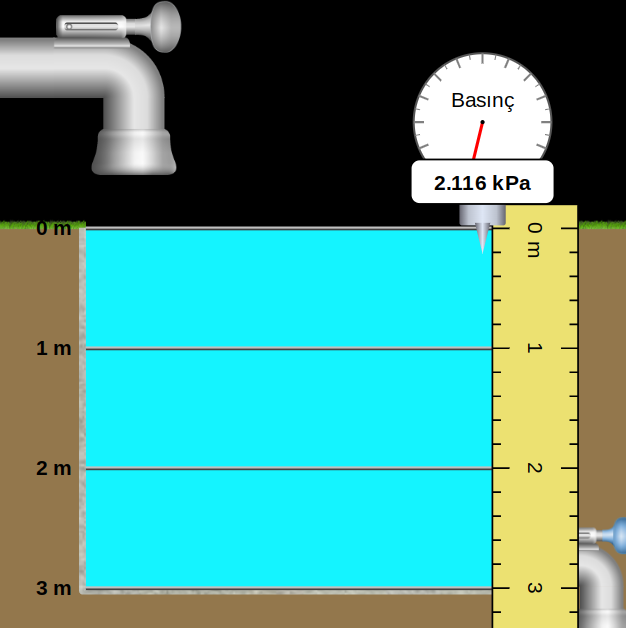
Basıncı ölçerken barometrenin en altındaki iğnesinin ölçmek istediğiniz derinlikle aynı hizada olduğuna dikkat etmelisiniz. Yukarıdaki şekilde 0,2 m için alınan basınç ölçümü gösteriliyor.

Veri Toplama

Aşağıda benim topladığım veriler görülüyor. Siz de simülasyonu kullanarak kendi verinizi toplayabilirsiniz.

Derinlik (m)	Basınç (kPa)
0	0
0,2	2,035
0,4	4,159
0,6	5,957
0,8	7,918
1	9,960
1,2	11,758
1,4	13,719
1,6	15,844
1,8	17,641
2	19,602
2,2	21,645
2,4	23,606
2,6	25,649
2,8	27,446
3	29,325

Veri Analizi

Derinliğin sıvı basıncına etkisini bulmak için tek bir ölçümün yeterli olduğunu düşünebilirsiniz. Basıncın derinliğe oranının bir olduğunu düşünüyorsanız, farklı derinlik ve basınç ölçümü çiftleri için bu hipotezi sınayabiliriz. Örneğin, (h = 0,4 m ve P = 4,159 kPa) çifti için oran = 4,159/0,4 = 10,4. Bir başka çift alalım, örneğin (h = 2,6 m ve P = 65,649 kPa) çifti için oran = 65,649/2,6 = 9,87. Yani oranlar tam olarak aynı değil. Daha güvenilir bir değer bulmak için derinlik – basınç grafiğini çizmeliyiz. Tablodaki verileri yerleştirip, bir de eğilim çizgisi eklediğimde grafik şöyle görünüyor.

 

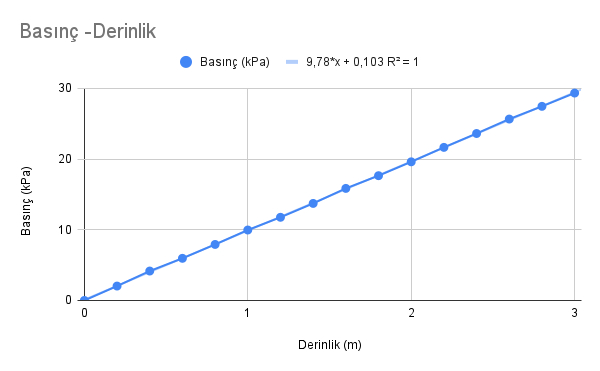
Bu grafiğin üstündeki formüller basınç ile derinliğin arasındaki matematiksel modeli veriyor. R¹ = 1, bu doğrusal model (yani çizgi) çok iyi oturmuş veriye demek.

basınç = 9,78 x derinlik + 0,103 (birim kPa). Basıncın birimini Pascal’a çevirmek için denklemin sağ ve sol taraflarını 1000’le çarpabiliriz.

basınç = 9708 x derinlik + 1030 (birim Pa).

Sonuç ve Değerlendirme

Peki grafiğin eğimi yani formüldeki katsayı olan 9,78 neyi veriyor? Grafiğin eğimini 9,78 bulduk. Ama birim analizi yapmadık, hemen yapalım.
[Pa] = [X][m]

[\frac{N}{m^2}] = [X][m] [X] = [\frac{N}{m^3}] = [\frac{\frac{kgm}{s^2}}{m^3}] = [\frac{kg}{m^3}][\frac{m}{s^2}]

X’in iki büyüklüğün çarpımı olarak yazılabileceğini bulduk. Bu büyüklüklerin ilki özkütle d, ikincisi ivme (bu durumda yerçekimi ivmesi g). Özkütle sıvının özkütlesi, biz su aldık sıvıyı, yani d = 1000 kg/m³. Yerçekimi ivmesini de g = 9.8 m/s² aldık. (Simülasyonda bunları bu şekilde seçerek kontrol ettik). Bu iki değişeni çarparsak:
d_{su} g = 1000 \times 9,8 = 9800 N/m^3

basınç = 9780 x derinlik + 1030

Deneysel olarak bulduğumuz değer 9870 N/m³, kuramdan hesapladığımız değer 9800 N/m³. Oldukça yakın sonuçlar. Hata oranımızı da hesaplayabiliriz.
\frac{\Delta (X)}{X} = \frac{9800 - 9780}{9800} = 0,002 = \%0,2

Yani deyedeki hatamız yüzde 0,2. Deneysel sonuçlarımız kuramla oldukça iyi uyum gösteriyor.

Peki araştırma sorumuza yanıt bulabildik mi? Bulduk. Sıvının derinliğiyle basıncı arasındaki ilişkinin doğrusal (yani doğru orantı şeklinde) olduğunu bulduk. Hipotezimizi de yanlışlayamadık. (Neden hipotezimizi doğruladık demedim? Cevaplarınızı yorumlarda bekliyorum.)

Deneyin videosu

Deney 3: Sıvının Özkütlesi Sıvı Basıncını nasıl etkiler?

Cevap aradığımız araştırma soruları şunlar olabilir:

1. Sıvının özkütlesiyle sıvının basıncı arasındaki ilişki nasıldır?
2. Sıvının basıncı sıvının özkütlesine göre nasıl değişir?

Hipotezimiz şöyle olabilir:

• Sıvının özkütlesi sıvının basıncıyla doğru orantılıdır. Özkütle arttıkça basınç da artar.

Deneyin Tasarımı

Simülasyon bize sıvının derinliğini kontrol etme olanağı sağlıyor. Öyleyse değişkenlerimizi belirleyelim:

Bağımlı değişkenimiz sıvı basıncı ve barometreyle ölçeceğiz.

Bağımsız değişkenimiz sıvının özkütlesi, simülasyon bize özkütleyi değiştirebileceğimiz bir kontrol düğmesi sağlıyor.

Kontrol değişkenleri: Sıvının derinliğini (h = 3 m), yerçekimi ivmesini (g = 9,8 m/s²), atmosferin varlığını ve sıvının bulunduğu kabın şeklini sabit tutacağız. Atmosfersiz ortamda doğrudan sıvının basıncını ölçebildiğimizi biliyoruz sıvı basıncına atmosferin etkisi deneyinden. Bu nedenle deneyi atmosfersiz ortamda yapacağız.

Deneyin İşlem Basamakları

1. Önce havuzun tamamını sıvıyla dolduralım.
2. Barometreyi havuzun tabanına yerleştirelim. h = 3 m olacak bu durumda.
3. Sıvının özkütlesini slider’ı en sola çekerek (benzin yazıyor burada) basıncı ölçelim. Ölçtüğümüz özkütle ve basınç değerlerini kaydedelim.
4. Sıvının özkütlesini 100’er 100’er artırarak üçüncü basamaktaki ölçümlerimizi alalım ve kaydedelim.

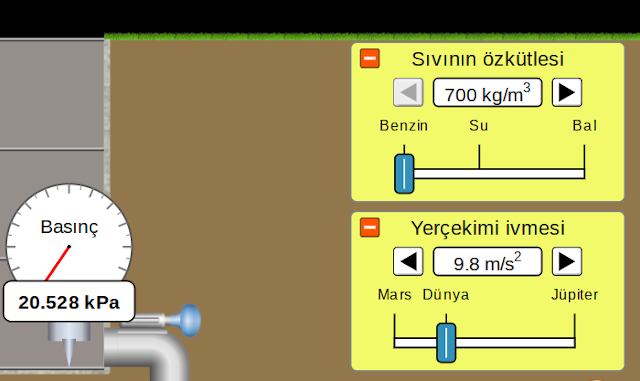
Yukarıdaki şekilde sıvının özkütlesini simülasyonda nasıl değiştirebileceğiniz gösteriliyor.

Veri Toplama

Aşağıda benim ölçtüğüm ve kaydettiğim veriler görülüyor. Siz de simülasyonu kullanarak kendi verilerinizi toplayabilirsiniz.

Özkütle (kg/m3)	Basınç (kPa)
700	20,528
800	23,460
900	26,393
1000	29,325
1100	32,258
1200	35,191
1300	38,123
1400	41,056

Veri Analizi

Tıpkı derinlik – basınç analizinde yaptığımız gibi bu kez de grafik çizeceğiz. Bu kez basınç – özkütle grafiğini çizmeliyiz. Benim çizdiğim grafik şöyle görünüyor:

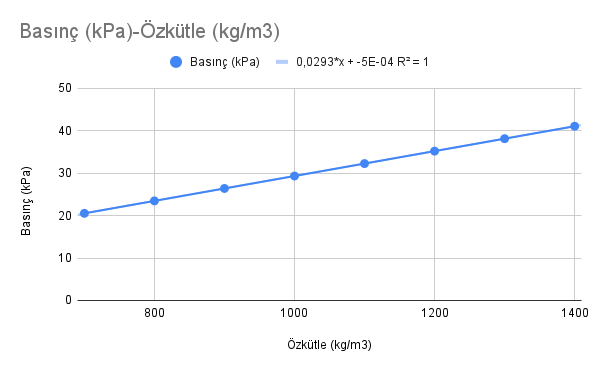
Yine bir eğilim çizgisi oturttuk veriye. Bu çizginin matematiksel modelini yazalım:

basınç = 0,0293 x özkütle (basıncın birimi kPa dikkat edin). Basıncın birimini Pa’ya çevirmek için eşitliğin iki yanını da 1000 ile çarpalım.

basınç = 29,3 x özkütle

Peki eğim bize ne veriyor? Yine birim analizi yapalım. X ile gösteriyoruz eğimi ve bunun birimini bulmaya çalışıyoruz.
[Pa] = [X][\frac{kg}{m^3}]

[\frac{N}{m^2}] = [X][\frac{kg}{m^3}] [X] = [\frac{Nm^3}{kgm^2}] = [\frac{Nm}{kg}] =[\frac{\frac{kgm^2}{s^2}}{kg}] = [m][\frac{m}{s^2}]

Eğimin birimi derinlikle yerçekimi ivmesinin çarpımı çıktı. Şimdi teoriden hesap yapıp deneysel sonucumuzla kıyaslayalım, bakalım ne kadar tutarlılar. Derinliği h = 3 m, yerçekimi ivmesini g = 9,8 m/s² almıştık. Demek ki teorik olarak bulmamız gereken değer:
3 \times 9,8 = 29,4 m^2/s^2

Deneysel olarak bulduğumuz değer buna çok yakın 29,3 m² / s².

Hata oranımızı hesaplayalım:
\frac{\Delta X}{X} = \frac{29,4 - 29,3}{29,4}= 0,003 = \%0,3

Deneysel sonuçlarımız teoriyle oldukça iyi uyum gösteriyor. Araştırma sorumuza cevap bulabildik mi? Evet. Sıvının özkütlesiyle basıncı arasındaki ilişkinin doğru orantılı olduğunu bulduk. Hipotezimizi de yanlışlayamadık. (Yine neden hipotezimizi doğruladık demedim? Cevaplarınızı yorumlarda bekliyorum.)

Deneyin videosu

Deney 4: Yerçekimi İvmesi Sıvının Basıncını nasıl etkiler?

Cevap aradığımız araştırma sorusu şöyle:

• Sıvının basıncı yerçekimi ivmesine göre nasıl değişir?

Hipotezimiz şöyle olabilir:

• Sıvının özkütlesi yerçekimi ivmesiyle doğru orantılıdır. Yerçekimi ivmesi arttıkça basınç da artar.

Deneyin Tasarımı

Simülasyon bize sıvının derinliğini kontrol etme olanağı sağlıyor. Öyleyse değişkenlerimizi belirleyelim:

Bağımlı değişkenimiz sıvı basıncı ve barometreyle ölçeceğiz.

Bağımsız değişkenimiz yerçekimi ivmesi. Simülasyonla bunu değiştirebiliyoruz.

Kontrol değişkenleri: Sıvının derinliğini (h = 3 m), sıvının özkütlesi (d = 1000 kg/m³), atmosferin varlığını ve sıvının bulunduğu kabın şeklini sabit tutacağız. Deneyi atmosfersiz ortamda yapacağız.

Deneyin İşlem Basamakları

1. Önce havuzun tamamını sıvıyla dolduralım.
2. Barometreyi havuzun tabanına yerleştirelim. h = 3 m olacak bu durumda.
3. Sıvının özkütlesini d = 1000 kg/m³ yapalım.
4. Yerçekimi ivmesini g = 4.0 m/s² den 24 m/s² ye kadar ikişer ikişer artıralım, her seferinde barometrenin okuduğu basınç değerini kaydedelim.

Veri Toplama

Aşağıda benim ölçtüğüm ve kaydettiğim veriler görülüyor. Siz de simülasyonu kullanarak kendi verilerinizi toplayabilirsiniz.

Yerçekimi ivmesi (m/s2)	Basınç (kPa)
4	11,968
6	17,953
8	23,937
10	29,921
12	35,905
14	41,889
16	47,874
18	53,858
20	59,842
22	65,826
24	71,810

Veri Analizi

Tıpkı özkütle – basınç analizinde yaptığımız gibi bu kez de grafik çizeceğiz. Bu kez basınç – yerçekimi ivmesi grafiğini çizmeliyiz. Benim çizdiğim grafik şöyle görünüyor:

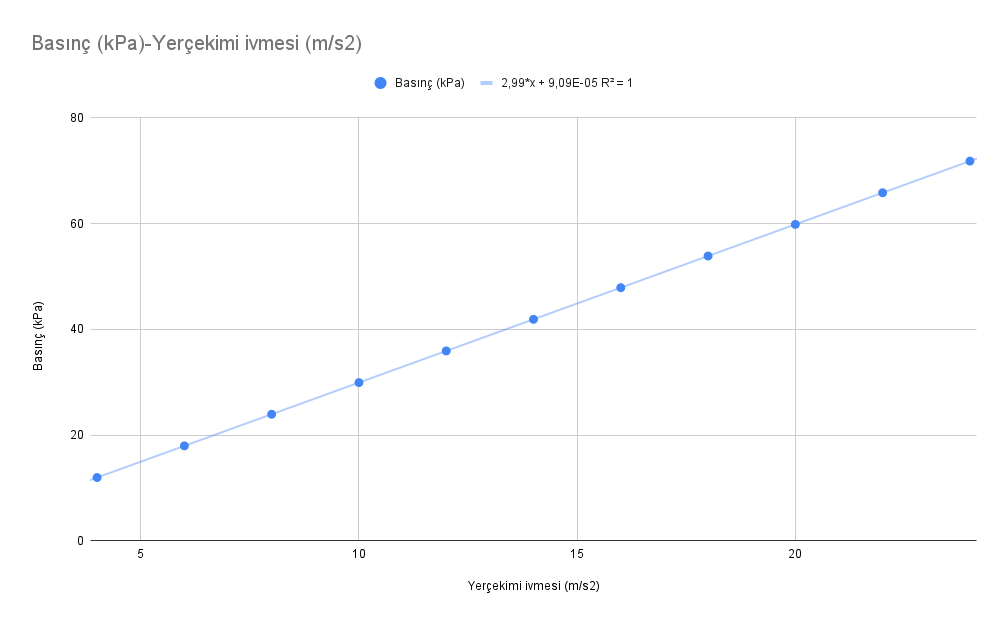
Veriye bir eğilim çizgisi oturttuk. Bu çizginin matematiksel modelini yazalım:

basınç = 2,99 x yerçekimi ivmesi (basıncın birimi kPa dikkat edin). Basıncın birimini Pa’ya çevirmek için eşitliğin iki yanını da 1000 ile çarpalım.

basınç = 2990 x özkütle

Peki eğim bize ne veriyor? Yine birim analizi yapalım. X ile gösteriyoruz eğimi ve bunun birimini bulmaya çalışıyoruz.
[Pa] = [X][\frac{m}{s^2}]

[\frac{N}{m^2}] = [X][\frac{m}{s^2}] [X] = [\frac{Ns^2}{m^3}] = [\frac{\frac{kgm}{s^2}s^2}{m^3}] = [\frac{kg}{m^2}] = [m][\frac{kg}{m^3}]

Eğimin birimi derinlikle özkütlenin çarpımı çıktı. Şimdi kuramdan hesap yapıp deneysel sonucumuzla kıyaslayalım, bakalım ne kadar tutarlılar. Derinliği h = 3 m, özkütleyi d = 1000 kg/m³ almıştık. Demek ki kuramsal olarak bulmamız gereken değer:
3 \times 1000 = 3000 kg/m^2

Deneysel olarak bulduğumuz değer buna çok yakın 2990 kg / m².

Hata oranımızı hesaplayalım:
\frac{\Delta X}{X} = \frac{3000 - 2990}{3000}= 0,003 = \%0,3

Deneysel sonuçlarımız kuramla epeyce iyi uyum gösteriyor. Araştırma sorumuza cevap bulabildik mi? Evet. Yerçekimi ivmesiyle sıvının basıncı arasındaki ilişkinin doğru orantılı olduğunu bulduk. Hipotezimizi de yanlışlayamadık.

Deneyin videosu

Simülasyon

Basınç altında PHET Simülasyonu’nu kullanarak siz de kendi deneylerinizi yapıp verinizi toplayabilirsiniz.

Sıvı Basıncı Deneyleri ile İlgili Kazanımlar

10.2.1.1. Basınç ve basınç kuvveti kavramlarının katı, durgun sıvı ve gazlarda bağlı olduğu değişkenleri açıklar.