Stroboskop, su dalgalarının hızı ve su dalgalarında kırılma

Bu yazıda su dalgalarının hızını hesaplamak için stroboskop adı verilen bir aracın nasıl kullanıldığını ve su dalgalarında kırılma olayını inceleyeceğiz. Hareket halindeki su dalgalarının hızı nasıl hesaplanabilir? Düzgün doğrusal hareketten ve dalgaların temel özelliklerinden şunları biliyoruz:

\Delta x = v \Delta t \lambda = vT f = \frac{1}{T}

Hızı bulmak için dalgaboyunu ve periyodu (ya da frekansı) bilmemiz gerekir.

v = \frac{\lambda}{T} = \lambda f

Öyleyse su dalgalarının hem dalgaboyunu hem de periyodunu ölçecek bir cihaza ihtiyacımız var. Bu cihaza stroboskop diyoruz.

Stroboskop nedir? Ne işe yarar?

Stroboskop merkezindeki eksen etrafında dönebilen, üzerinde eşit aralıklarla açılmış yarıklar bulunan daire şeklindeki bir ölçüm aracıdır. Aşağıdaki resimde bir stroboskop gösteriliyor. Ortasındaki deliğe parmağınızı yerleştirip stroboskopu döndürürsünüz. Sonra yarıkların arasından gözlemek istediğiniz dalgaya bakarsınız.

Aşağıdaki resimde su dalgalarına stroboskobun arkasından bakıyoruz. Dalga leğeninin altındaki dairesel su dalgalarının sanki duruyormuş gibi göründüğüne dikkat edin.

Dalgalar neden duruyormuş gibi görünüyor?

1. Stroboskop dönerken bir yarıktan diğerine gelene kadar görüş alanımızı kapatıyor.
2. Stroboskobun ilk yarığında ilk dalganın tepesini veya çukurunu görüyoruz.
3. Stroboskop ilk yarıktan ikinci yarığa gelene kadar görüş alanımızı kapatıyor. Bu sırada dalga bir dalgaboyu ilerliyor.İlerlediği sırada dalgayı göremiyoruz.
4. Stroboskop ikinci yarığa ulaştığında ikinci dalganın tepesini veya çukurunu ilk dalganın aynı yerinde görüyoruz. İşte bu nedenle stroboskobun iki ardışık yarığının arasında geçen süre dalganın periyoduna eşit olduğunda dalgayı duruyormuş gibi görüyoruz.

Stroboskopun bir tam tur süresini (periyodunu) bilirsek su dalgalarının periyodunu da hesaplayabiliriz. (Düzgün çembersel harekette bunu daha ayrıntılı öğreneceksiniz.) Bunun için stroboskopun periyoduyla dalganın periyodu arasındaki ilişkiyi anlamamız gerekli. Tekrarlayalım: iki ardışık yarık arasındaki sürenin dalganın periyoduna eşit olması gerekiyor. Peki iki ardışık yarık arasındaki süreyi nasıl bulabiliriz?

Yukarıdaki resimlerdeki stroboskopların toplam 12 yarığı var. Bu yarıkların birbirlerine olan mesafeleri eşit (yani açıları eşit). Eğer stroboskobun bir tam tur süresine (periyoduna) T_stroboskop dersek iki yarık arasında geçen süre T_stroboskop/12 olur. Buradan:

T_{dalga} = \frac{T_{stroboskop}}{12}

Eğer bu ifadeyi genellersek yani yarık sayısına n dersek:

T_{dalga} = \frac{T_{stroboskop}}{n}

Ayrıca dalga leğeninin altına bir cetvel yerleştirip stroboskopla bakarak dalgaboyunu ölçebiliriz. Periyodu ve dalgaboyunu ölçebildiğimize göre dalganın sudaki hızını da hesaplayabiliriz. Aslında öğretim programında matematiksel işlemler yok, ama iyice anlamak için bir tane soru çözelim.

Örnek soru: stroboskop ve su dalgasının hızı

Bir dalga leğeninde oluşturulan su dalgalarının hızını hesaplamaya çalışan bir grup öğrenci 6 yarıklı bir stroboskop kullanıyor. Stroboskoptan bakarken dalgaları hareketsiz gördükleri sırada stroboskobun bir tam devir süresini 3 saniye olarak ölçüyorlar. Dalga leğeninin altında 5 dalga tepesi arasındaki uzaklığı 20 cm ölçtüklerine göre, dalgaların hızı kaç cm/s dir?

Çözüm:

Stroboskobun periyodunu biliyoruz. Öyleyse iki yarık arasında geçen süreyi yani dalgaların periyodunu hesaplayabiliriz:

T_{dalga} = \frac{T_{stroboskop}}{n} n = 6; T_{stroboskop} = 3 \space s T_{dalga} = \frac{3 \space s}{6} = 0,5 \space s

5 dalga tepesi 4 tam dalgaya karşılık gelir. (Bunu bir düşünün neden?) Öyleyse dalgaboyunu da hesaplayabiliriz:

\lambda = \frac{20 \space cm}{4} = 5 \space cm

Artık dalgaların hızını bulabiliriz:

v = \frac{\lambda}{T_{dalga}} v=\frac{5 \space cm}{0,5 \space s} = 10 \space cm/s

Su dalgalarının hızı ve ortamın derinliği

Su dalgalarının hızının nasıl ölçülebildiğini (yani aslında hesaplanabildiğini) gördük. Peki suyun derinliğiyle su dalgalarının hızı arasında bir ilişki var mıdır? Su dalgaları her derinlikte aynı hızla mı ilerler, yoksa derinliğe göre hızlanır veya yavaşlar mı?

Yukarıdaki videoda su dalgalarının derin ve sığ ortamlarda nasıl ilerlediği görülüyor. Dalga leğeninin içine bir cam levha yerleştirilerek sağ tarafı daha sığ hale getirilmiş.

Su dalgalarının dalgaboyunun derin ortamda sığ ortama göre daha büyük olduğunu görüyoruz.

Su dalgaları için ortam farklılığının nedeni derinliktir. İki ortamı birbirinden ayıran yüzeyin normali ile aynı doğrultuda ilerleyen doğrusal su dalgaları doğrultu değiştirmeden birinci ortamdan ikinci ortama geçer. Aşağıdaki resimde bu durum gösteriliyor.

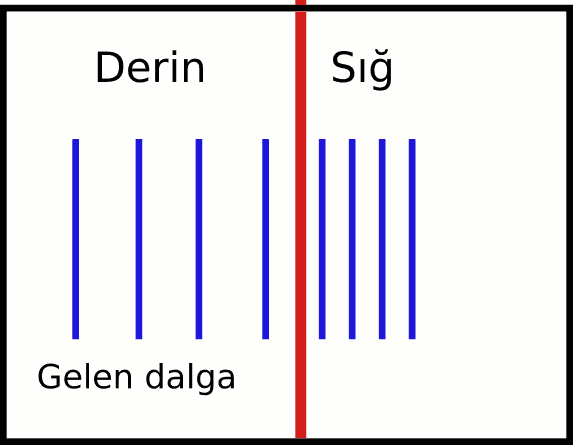
Su dalgalarının derinliği farklı ortamlarda dalgaboyları değişir, çünkü su dalgaları farklı ortamlarda farklı hızda yayılır. Ortamın değişmesi frekansı etkilemez. Çünkü bir dalganın frekansı, yalnızca dalga kaynağının frekansına bağlıdır.

Dalgaboyunun sığ ortamda derin ortamdan daha küçük olduğunu videoda gördük. Öyleyse:

\lambda = \frac{v}{f} \lambda_{SIG} < \lambda_{DERIN} v_{SIG} < v_{DERIN}

Yani sığ ortamda su dalgalarının hızı da derin ortama göre daha küçüktür. Su dalgaları derin ortamdan sığ ortama geçerken yavaşlar.

Su dalgalarında kırılma

Su dalgalarının bir ortamdan diğerine geçerken yön değiştirmesine kırılma denir. Bir önceki bölümde su dalgaları derin ortamdan sığ ortama gelirken ortamların normaline dik geliyorlardı. Şimdi normalle bir açı yaparak geldiklerinde nasıl kırıldıklarına bakalım.

Aşağıdaki videoda su dalgalarının derin bir ortamdan sığ bir ortama geçerken nasıl kırıldığı gösteriliyor. Derin ve sığ ortam arasına çizilen normal doğrusu ile su dalgalarının geliş doğrultusunun yaptığı açı geliş açısı, sığ ortamda su dalgalarının ilerleme doğrultusu ile normalin yaptığı açı ise kırılma açısı.

Aşağıdaki resimde su dalgalarının derin ortamdan sığ ortama geçerken kırılmasını görüyoruz.

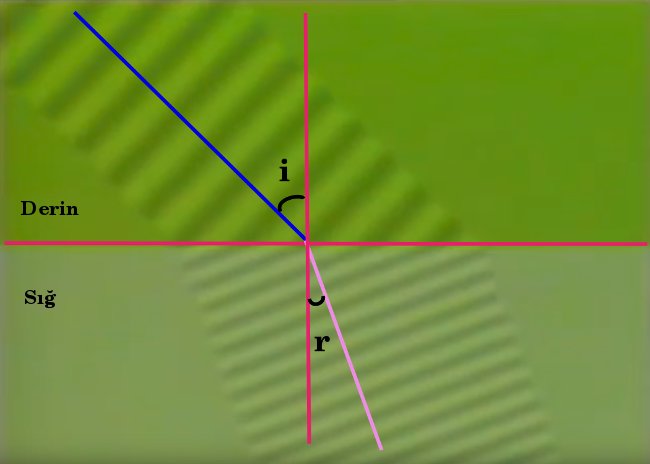
Derin ve sığ ortamı birbirinden ayıran yüzeyin normali ile belirli bir açı oluşturarak gelen su dalgaları ikinci ortama geçerken doğrultu değiştirir. Su dalgaları derin ortamdan sığ ortama geçerken normale yaklaşarak kırılır. Bu durumda i > r yani geliş açısı kırılma açısından daha büyük.

Aşağıdaki resimde su dalgalarının sığ ortamdan derin ortama geçerken kırılmasını görüyoruz.

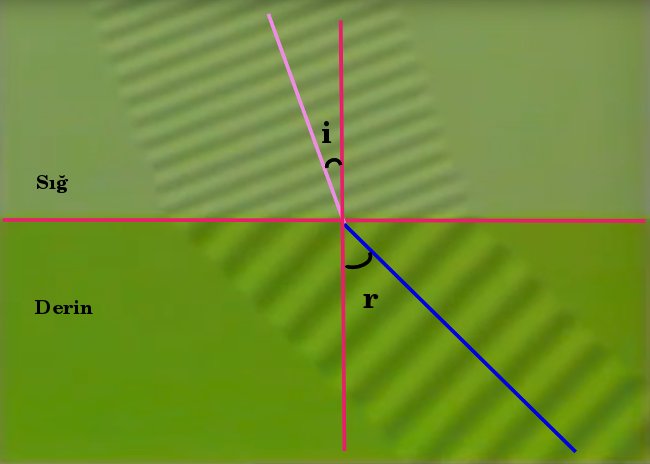
Su dalgaları sığ ortamdan derin ortama geçerken normalden uzaklaşarak kırılır. Yani bu kez i < r gelme açısı kırılma açısından daha küçük olur.

Daha sonra ışıkta kırılma olayını öğrenirken, dalgaların kırılmasıyla neredeyse tamamen aynı olduğunu leşfedeceksiniz.

Su dalgalarının hızı ve kırılma ile ilgili kazanımlar

10.3.3.3. Ortam derinliği ile su dalgalarının yayılma hızını ilişkilendirir.

• Öğrencilerin deney yaparak veya simülasyonlarla ortam derinliğinin dalganın hızına etkisini incelemeleri ve dalga boyundaki değişimi gözlemlemeleri sağlanır.
• Ortam değiştiren su dalgalarının dalga boyu ve hız değişimi ile ilgili matematiksel hesaplamalara girilmez.
• Stroboskopun dalga boyu ölçümünde kullanıldığından bahsedilir, matematiksel hesaplamalara girilmez.

10.3.3.4. Doğrusal su dalgalarının kırılma hareketini analiz eder.

• Öğrencilerin deney yaparak veya simülasyonlar kullanarak su dalgalarının kırılma hareketlerini çizmeleri sağlanır.
• Dairesel su dalgalarının kırılması konusuna ve matematiksel hesaplamalara girilmez.