Tork nedir? Örnek sorular ve çözümleri

Bir şeyin hareket etmesini sağlamak için kuvvet gerekir. Bir şeyin dönmesini sağlamak için de tork gerekir. Tork, kuvvetin bir cismi bir eksen etrafında döndürme etkisidir. Tork, dönme momenti ya da kuvvet momenti olarak da bilinir. Bunu bir örnekle anlatalım. Aşağıda ağır bir kapının üstten görünüşü var. Kapıyı döndürebilmek için kapının bir nokta ya da bir eksen etrafında serbestçe hareket etmesini sağlamak gerekir. Kapının menteşelerinin bulunduğu sabit eksen, dönme eksenidir. Kapı, bu eksen etrafında döner. Eşit büyüklükte dört kuvvet kapının farklı noktalarına uygulanıyor. Bu kuvvetlerden hangisi kapıyı daha kolay döndürür?

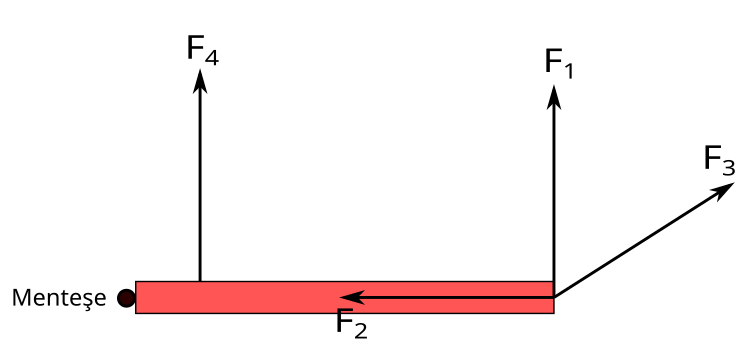
F₁ kuvveti kapının dönüp açılmasını sağlar. Ama F₂ menteşeye doğru yöneldiği için kapıyı döndürüp açamaz. F₃ kuvveti de kapının açılmasını sağlar, ama kapıya dik olmadığı için F₁ kadar etkili değildir. F₄ kuvveti eşit büyüklükte ve kapıya dik olmasına rağmen menteşeye yakın olduğu için kapıyı açmakta zorlanmamıza neden olur.

Tork nelere bağlıdır?

Bir kuvvetin dönmeye neden olabilmesi üç değişkene bağlıdır:

1. Kuvvetin büyüklüğü.
2. Kuvvetin uygulandığı noktanın, döndürme noktasına yani cismin dönebileceği eksene uzaklığı.
3. Kuvvetin uygulandığı açı.

Torkun yönü nasıl belirlenir?

Tork Yunan harfi tau (τ) ile gösterilir, vektörel ve türetilmiş bir büyüklüktür. Torkun birimi N.m’dir ve matematiksel modeli yani torkun formülü şöyledir:
\vec{\tau} = \vec{r} \times \vec{F}

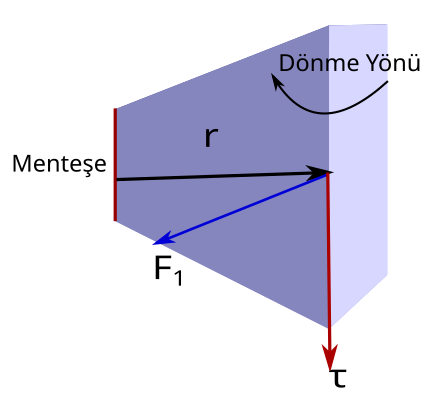
Yani tork, dönme ekseninden uzaklık vektörüyle (r), uygulanan kuvvet vektörünün (F) vektörel çarpımına eşittir. Vektörel çarpımın sonucu yine bir vektör verir, bu vektör çarpılan vektörlerin her ikisine de diktir. Sağ el kuralını kullanarak torkun yönünü bulabiliriz. Bunu yine yukarıdaki kapı örneğiyle gösterelim, sadece F₁ kuvvetini kullanalım. Bu kez aynı kapıya yandan bakıyoruz.

r vektörü dönme noktasından (menteşeden) kuvvetin uygulandığı noktaya uzanan konum vektörü. F₁ kuvvet vektörü, konum vektörüne (r) dik. τ = r x F₁ olan tork vektörü her iki vektöre dik ve +z yönünde (+z yönünü yukarı yön olarak alıyoruz). Kapının dönme yönü bize tork vektörünün yönünü gösteriyor. Kapı saat yönünün tersinde döndüğü için tork vektörü de +z yönünde. Bu durumda kapıyı itmişiz. Aşağıdaki resimde tork vektörünün yönünü sağ el kuralıyla nasıl bulabileceğimiz gösteriliyor. C vektörün yönü tork vektörünün yünüyle aynı.

Peki ya aynı kuvvetle aynı noktadan kapıyı çekseydik, yani F₁ kuvvet vektörünün yönünü zıt yapsaydık ne olurdu?

Bu kez kapının saat yönünde döndüğünü farketmiş olmalısınız. Sağ el kuralına göre torkun yönü de -z eksenine (yani aşağıya) doğru oldu. Tork vektörünün kapının dönme ekseni üzerinde olduğunu da söyleyelim. Vektörlerin taşınabildiğini hatırlayın. Aşağıdaki resim de dönme yönü zıt olduğunda sağ el kuralıyla tork vektörünün yönünü nasıl bulabileceğimizi gösteriyor.

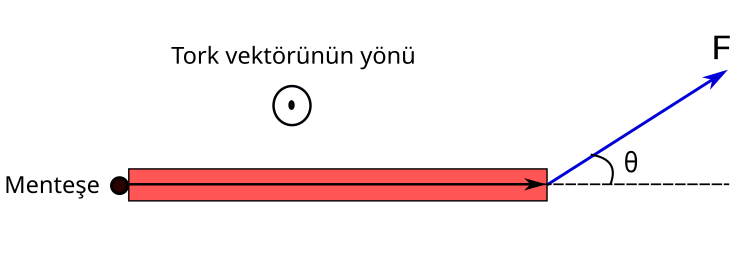
Peki kapıya üstten baktığımızda tork vektörünün yönünü nasıl göstereceğiz. Bunun cevabı ya sayfa düzleminden dışarı doğru ya da sayfa düzleminde içeri doğru olacak. Bu iki durumu da resimlerle gösterelim. Aşağıdaki resimde kuvvet kapıyı saat yönünün tersinde çeviriyor. Eğer sağ el kuralını kullanırsanız başparmağınızın size dönük olduğunu göreceksiniz. Yani tork vektörü sayfa düzlemine dik ve dışarı doğru. Bunu bir çemberin içine çizilmiş nokta işaretiyle gösteriyoruz. Hatırlamak için bir okun size gelen ucunu gördüğünüzü hayal edebilirsiniz.

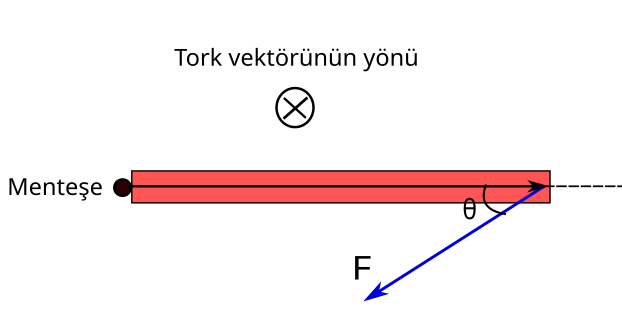
Aşağıdaki resimde ise kuvvet kapıyı saat yönünde döndürüyor. Sağ el kuralını kullandığınızda başparmağınızın size dönük olmadığını sayfanın içine dönük olduğunu göreceksiniz. Yani bu kez tork vektörü sayfa düzlemine dik ve sayfanın içine doğru. Bunu bir çemberin içine çizilmiş çarpı işaretiyle gösteriyoruz. Hatırlamak için bir okun arkasını gördüğünüzü hayal edebilirsiniz.

Torkun büyüklüğü nasıl bulunur?

Torkun yönünü bulmayı öğrendiğimize göre, artık büyüklüğünü bulmaya da geçebiliriz. Bunu da yine kapı örneğiyle gösterelim.

Yine kapıya yukarıdan bakıyoruz. r konum vektörünün doğrultusuyla kuvvet vektörü F’in arasında θ açısı var. Vektörel çarpımdan torkun büyüklüğünü bulabiliriz:
|\vec{\tau}| = |\vec{r}||\vec{F}|sin \theta

Yani konum ve kuvvet vektörlerinin büyüklüklerini çarpıp, aralarındaki açının sinüsüyle tekrar çarpıyoruz. Konum ve kuvvet vektörlerinin arasındaki açı 90° olursa sin90° = 1 olduğu için torkun büyüklüğü bu iki vektörün büyüklüklerinin çarpımına eşit oluyor.

Torku hesaplamayı kolaylaştırmak için kuvvetin konum vektörüne göre dik bileşeniyle çarpımı kullanılabilir. Aşağıdaki resimde bu durumu görüyoruz.

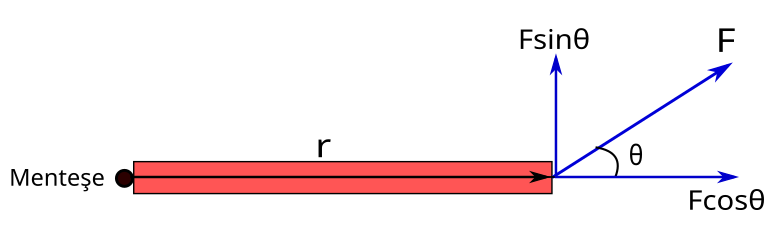
Fsinθ konum vektörüne dik olan kuvvet bileşeni. Dolayısıyla tork = rFsinθ oluyor. Fcosθ ise konum vektörüne paralel, yani açısı 0. sin 0° = 0 olduğu için kuvvetin bu bileşeninin döndürme etkisi yok, yani paralel bileşenin torku sıfır.

Tork ile kuvvet arasındaki fark

Kuvvet herhangi bir noktaya uygulanabilir, 10 N kuvvet kendi başına bir kuvveti ifade eder. Ama tork kendi başına pek birşey anlatmaz. Yani 20 N.m tork uyguladım diyebilmeniz için hangi dönme noktasına ya da dönme eksenine göre torku belirlediğinizi söylemeniz gerekir. Çünkü başka bir nokta seçerseniz konum vektörü (r) ve açı değişir, dolayısıyla tork da değişir.

Örnek soru 1

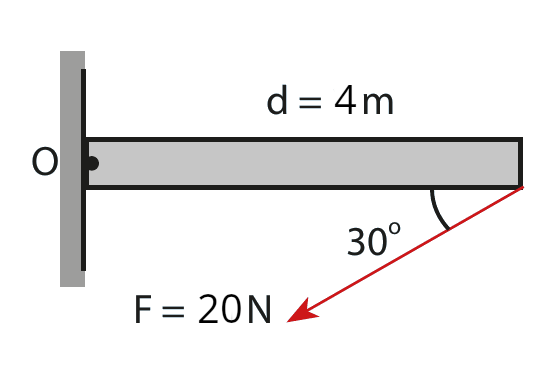
Şekildeki 4 m uzunluğundaki çubuk O noktası etrafında rahatça hareket edebilmektedir. Bu çubuğun ucuna şekildeki gibi uygulanan 20 N büyüklüğündeki F kuvvetinin uyguladığı torkun yönü ne tarafa doğrudur ve büyüklüğü kaç N.m’dir?

Çözüm

• Sağ el kuralını kullanarak torkun yönünü bulabiliriz. Çubuk saat yönünde dönüyor öyleyse torkun yönü sayfa düzleminden içeri doğru.
• Şimdi de büyüklüğünü hesaplayalım. Vektörel çarpımdan büyüklüğü biliyoruz:

\tau = rFsin\theta \tau = (4m)(20N)sin30^\circ = 80\frac{1}{2} = 40 Nm

Net tork (bileşke tork) nasıl bulunur?

Net tork (toplam tork ya da bileşke tork da denir), bir cisme uygulanan kuvvetlerin aynı dönme noktasına (eksenine) göre torklarının vektörel toplamı hesaplanarak bulunur.
\vec{\tau_{net}} = \vec{\tau_1} + \vec{\tau_2} + .. +\vec{\tau_n}

Net torkun nasıl bulunduğunu bir örnek soruyla görelim.

Örnek soru 2

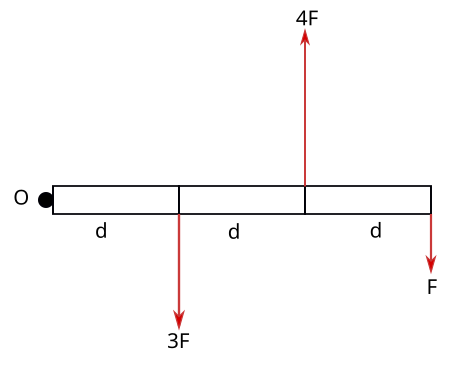
Şekilde gösterilen O noktası etrafında rahatça dönebilen ağırlıksız çubuk eşit bölmelerle ayrılmıştır. Şekilde gösterilen kuvvetler bu çubuğa uygulandığında net torkun yönü hangi yön ve büyüklüğü kaç Fd olur?

Çözüm

Sırayla kuvvetlerin O noktasına göre torklarını bulacağız. Yönlerine dikkat etmemiz lazım. Hangi kuvvetten başladığımız önemli değil ama sistemli gitmek için O noktasına en yakın olan kuvvetten başlayalım. Tüm kuvvetler konum vektörüne dik bu nedenle sin90 = 1 ile sinüs’ten kurtulmuş oluyoruz.
\tau_1 = 3Fd(sin90^\circ) = -3Fd

Birinci kuvvet saat yönününde döndürüyor, bu nedenle işareti eksi.
\tau_2 = (4F)(2d) = 8Fd

İkinci kuvvet saat yönünün tersinde döndürüyor, işareti artı.
\tau_3 = -F(3d) = -3Fd

Üçüncü kuvvet saat yönününde döndürdüğü için işareti eksi. Şimdi net torku bulabiliriz:
\tau_{net} = -3Fd + 8Fd + (-3Fd) = 2Fd

Net torkun yönünün artı olduğunu yani sayfa düzleminden dışarı doğru olduğunu bulduk, toplamda çubuk saat yönünün tersinde dönüyor. Ayrıca net torkun büyüklüğünün de 2Fd olduğunu hesapladık.

Tork ile ilgili kazanımlar

11.1.8.1. Tork kavramını açıklar.

• Torkun yönünü belirlemek için sağ el kuralı verilir.

11.1.8.2. Torkun bağlı olduğu değişkenleri analiz eder.

• Öğrencilerin deney yaparak veya simülasyonlar kullanarak torkun bağlı olduğu değişkenler ile ilgili sonuçlar çıkarmaları sağlanır.