Vektörler: Çizimi, tanımı, özellikleri ve örnek soru çözümleri

En genel anlamıyla vektör, uzayda yönlendirilmiş doğru parçasıdır. Fizikte, büyüklüğü (şiddeti ya da uzunluğu) ve yönü olan büyüklüklere (niceliklere) vektörel büyüklük denir. Skaler büyüklükler sadece bir sayı ile ifade edilebilirken, vektörler sayının yanında başlangıç (uygulama) noktası, doğrultu ve yön bilgisi içerir. Örneğin, kuvvet vektördür. Birinin “ben 50 N kuvvet uyguladım” demesi yetmez. Uyguladığı kuvveti tam olarak anlatabilmesi için “Ben 50 N kuvveti cismin orta noktasına, doğu – batı doğrultusunda, doğuya doğru uyguladım” demesi gerekir.

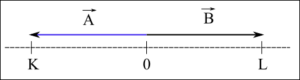
Vektörler bir okla gösterilir, okun başlangıç noktası uygulama yerini, okun ucu vektörün yönünü gösterir. Aşağıdaki şekilde bir boyutta \vec{A} ve \vec{B} vektörleri gösteriliyor:

• Vektörel büyüklüklerin simgelerinin üstünde vektör olduklarını gösteren bir ok bulunur: \vec{A} gibi.
• Mutlak değerleri uzunluklarını gösterir: |\vec{A}| = A gibi. Yalnızca A olarak ifade edildiklerinde uzunlukları kastedilir.
• O noktası \vec{A} ve \vec{B} vektörlerinin de uygulanma noktasıdır
• Kesikli çizgilerle gösterilen doğru her iki vektörün de doğrultusudur, ama yönü değildir. Bu iki vektör aynı doğrultudadır, yani birbirine paraleldir.
• \vec{A} vektörünün yönü sola doğrudur, okun ucu solu gösteriyor.
• |OK| doğru parçasının uzunluğu \vec{A} vektörünün büyüklüğüdür |\vec{A}|.
• \vec{B} vektörünün yönü sağa doğrudur, okun ucu sağı gösteriyor.
• |OL| doğru parçasının uzunluğu \vec{B} vektörünün büyüklüğüdür |\vec{B}| .

Kartezyen Koordinat Sistemi

Kartezyen ya da dik koordinat sistemi bir cismin uzaydaki yerini belirlemek için kullanılan bir sistemdir. Birbirine dik eksenlerin kesişme noktaları orijin (başlangıç) noktası olarak alınır. Orijinin koordinatları iki boyutta (0,0) yani x=0 ve y=0, üç boyutta (0,0,0) yani x=0, y=0 ve z=0 olarak alınır ve O harfiyle gösterilir. Orijin genellikle referans noktası olarak kabul edilir.

İki boyutlu kartezyen koordinat sisteminde bir vektör, orijinden (0,0) vektörün bitiş noktasının koordinatlarına (x,y) bir ok çizilerek gösterilir. Aşağıdaki şekilde \vec{K} vektörü gösteriliyor.

 

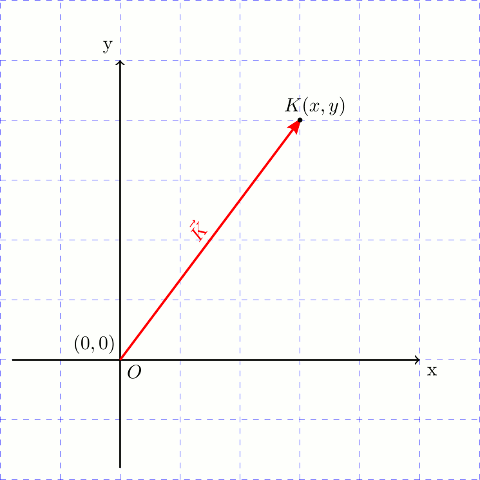
Üç boyutlu kartezyen koordinat sisteminde (x,y ve z eksenleri birbirine diktir), bir vektör, orijinden (0,0,0) vektörün bitiş noktasının koordinatlarına (x,y,z) bir ok çizilerek gösterilir. Aşağıdaki şekilde \vec{L} vektörü gösteriliyor.

 

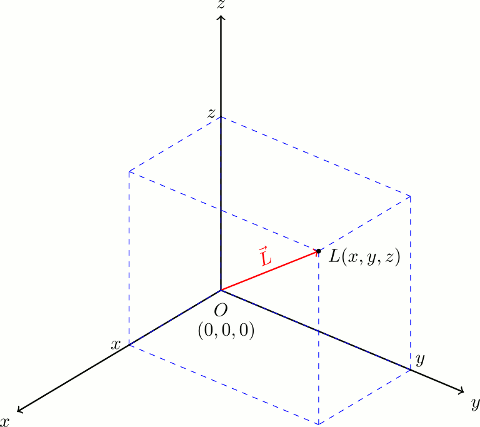
Eşit vektörler ve Zıt vektörler

Eğer iki vektörün doğrultusu, yönü ve büyüklüğü aynı ise bunlara eşit vektörler ya da özdeş vektörler denir. Eşit vektörlerin uygulama noktaları farklı olabilir. Eşit vektörler matematiksel olarak şöyle gösterilir:

\vec{K} = \vec{L} (vektörlerin üstlerindeki oklara dikkat etmelisiniz.)

Ayrıca eşit vektörlerin uzunlukları (büyüklük ya da şiddet de denir) da eşittir: |\vec{K}|=|\vec{L}| ve K=L.

Aşağıdaki resimde \vec{K} ve \vec{L} vektörleri birbirine eşit. Çünkü, aynı doğrultudalar (-x +x doğrultusu), yönleri aynı (+x yönündeler) ve aynı büyüklükteler (3 birim kare).

 

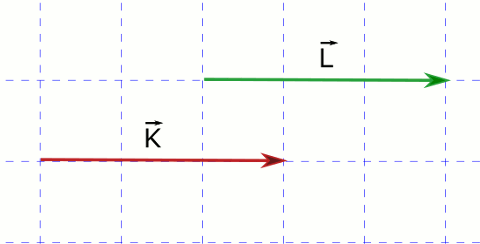
Eğer iki vektörün doğrultuları ve büyüklükleri aynı ama yönleri zıt ise bunlara zıt vektörler denir. Zıt vektörlerin de uygulama noktaları farklı olabilir.

Zıt vektörlere negatif vektörler de denir, matematiksel olarak şöyle gösterilir. (Eksi işaretine dikkat etmelisiniz, zıt eksi işaretli demek.)

\vec{M} = -\vec{N}

Aşağıdaki resimde \vec{M} ve \vec{N} vektörleri birbirlerine zıt. Doğrultuları aynı (-x +x doğrultusu), büyüklükleri aynı (2 birim) ama yönleri zıt. \vec{M} +x yönündeyken, \vec{N} -x yönünde.

 

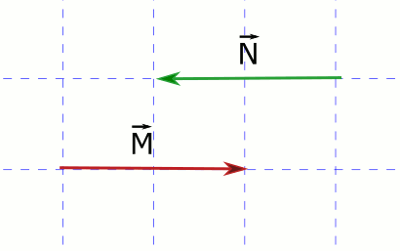
Bir vektörün negatifini almak (eksi işaretli yapmak), vektörün yönünü değiştirmek demektir.

Vektörün Skalerle Çarpımı

Bir vektörü pozitif skaler bir nicelikle (yani sayıyla çarpmak) vektörün büyüklüğünü çarpıldığı sayıyla orantılı olarak değiştirir.

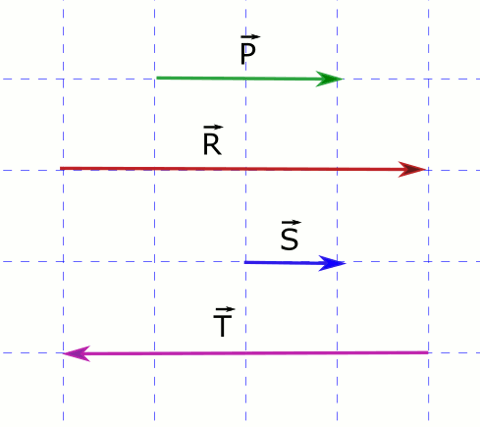
Yukarıdaki resimde büyüklüğü 2 birim kare olan \vec{P} vektörünü 2 ile çarpınca, büyüklüğü 4 birim kare olan \vec {R} vektörü; \frac{1}{2} ile çarpınca, büyüklüğü 1 birim kare olan \vec{S} vektörü elde ediliyor.

\vec{R} = 2\vec{P} \space ve \space \vec{S} = \frac{1}{2}\vec{P}

Eğer bir vektörü -1 ile çarparsanız, yönünü değiştirirsiniz. Eğer başka bir negatif sayıyla çarparsanız hem yönünü değiştirirsiniz hem de çarptığınız sayıyla orantılı olarak büyüklüğünü değiştirirsiniz. Yukarıdaki resimde +x yönünde 2 birim uzunluğundaki \vec{P} vektörü -2 ile çarpılınca -x yönünde 4 birim uzunluğundaki \vec{T} vektörü elde edilmiş.

\vec{T} = -2\vec{P}

Örnek Soru Çözümü 1: Eşit ve Zıt Vektörler

Büyüklükleri sıfırdan farklı \vec{E} ve \vec{F} vektörleri için aşağıdaki bilgilerden hangisi kesinlikle doğrudur?

A) Uzunlukları eşitse kesinlikle eşit vektörlerdir.

B) Zıt vektörlerse \vec{E} = \vec{F} dir.

C) Zıt vektörlerse yönleri aynıdır.

D) Zıt vektörlerse \vec{E} // \vec{F} dir.

E) Eşit vektörlerse yönleri zıttır.

Çözüm:

• Uzunlukları aynı olursa, eşit ya da zıt vektör olabilirler. Kesinlikle eşit olmak zorunda değiller.
• Zıt vektörlerse \vec{E} = \vec{-F} olması gerekir, eksi işareti yok.
• Zıt vektörlerin yönleri zıttır, aynı değildir.
• D şıkkı doğru, zıt vektörler aynı doğrultudadır, birbirine paraleldir yani.
• Eşit vektörlerin yönleri aynıdır, zıt değildir.

Örnek Soru Çözümü 2: Vektörler ve büyüklük

Bir vektör çiziliyor ve M olarak adlandırılıyor.

Buna göre aşağıdaki gösterimlerden hangisi vektörün şiddetini göstermek için kullanılabilir.

I. \vec{M}

II. M

III. |\vec{M}|

A) Yalnız I

B) Yalnız II

C) Yalnız III

D) I ve II

E) II ve III

Çözüm:

Vektörün büyüklüğü (şiddeti veya uzunluğu da dendiğini hatırlayın) üzerinde ok olmayan harfiyle ya da mutlak değer içinde üzerinde ok olan harfiyle gösterilir. Yani M \space veya \space|\vec{M}| ile vektörün büyüklüğü gösterilebilir. Doğru cevap E.

Vektörler ile ilgili Simülasyon

Vektörlerin özellikleri, eşit ve zıt vektörleri deneyerek görebileceğiniz şu simülasyonu öneriyoruz: Vektör Toplama PHET Simülasyonu

Vektörler ile ilgili Fizik Dersi Kazanımları

11.1.1.1. Vektörlerin özelliklerini açıklar.
11.1.1.2. İki ve üç boyutlu kartezyen koordinat sisteminde vektörleri çizer.