Bir vektörün bileşenleri, o vektörün kartezyen koordinat sistemindeki eksenler üzerindeki izdüşümleridir. Kartezyen koordinat sisteminde eksenlerle açı yapan vektörlerin bileşenlerine ayrılması, vektörlerin toplanması ve çıkarılmasında kolaylık sağlar. Böylece çok sayıda vektörün bileşkesini uç uca ekleme ya da paralel kenar yöntemlerini kullanmadan kolayca bulabiliriz.
Aşağıdaki resimde kırmızı olarak gösterilen \vec{K} vektörü x ekseniyle \theta açısı yapıyor , büyüklüğü K.
- \vec{K} vektörünün x – eksenine izdüşümü \vec{K_x} vektörü, büyüklüğü K_x.
- \vec{K} vektörünün y- eksenine izdüşümü \vec{K_y} vektörü, büyüklüğü K_y
- \vec{K} = \vec{K_x}+\vec{K_y} olduğuna dikkat etmelisiniz. İzdüşüm vektörlerinin toplamı vektörün kendisine eşit olduğu için bileşenlerine ayırabiliyoruz.
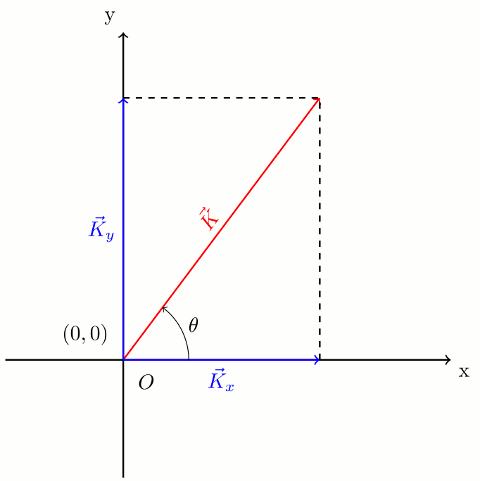
x ve y eksenleri birbirine dik olduğu için, dik üçgen bağıntılarını kullanarak, bileşenlerin büyüklüklerini ayrıştırdığımız vektörün büyüklüğü cinsinden hesaplayabiliriz.
cos\theta = \frac{K_x}{K} yani K_x = Kcos\theta
sin\theta = \frac{K_y}{K} yani K_y = Ksin\theta
Bu iki bileşen hipotenüsünün uzunluğu K olan bir dik üçgenin iki kenarını oluşturur, Pisagor bağıntısından:
K = \sqrt{K_x^2 + K_y^2}Örnek soru 1: Vektörün bileşenleri nasıl hesaplanır?
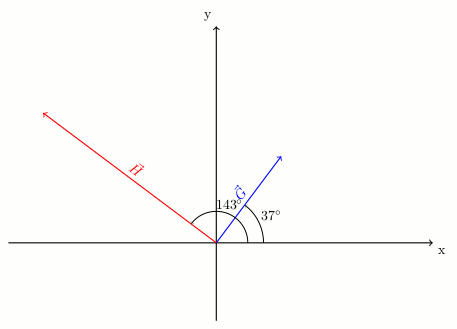
Yukarıdaki şekilde gösterilen \vec{G} vektörünün büyüklüğü 10 birimdir ve x ekseniyle yaptığı açı 37^\circ dir. \vec{H} vektörünün büyüklüğü 20 birimdir ve x ekseniyle 143^\circ açı yapmaktadır. Bu iki vektörün bileşenlerinin büyüklüklerini bulunuz. (cos37^\circ = 0,8 \space ve \space sin37^\circ = 0,6 alınız.)
Çözüm:
Bir vektörün x bileşeninin büyüklüğünün nasıl bulunduğunu öğrendik. \vec{G} vektörününküleri bulalım:
|\vec{G_x}| = |\vec{G}|cos37^\circ|\vec{G_x}| = 10(0,8) = 8 birim.
y bileşenini bulmak da kolay:
|\vec{G_y}| = |\vec{G}|sin37^\circ|\vec{G_y}| = 10(0,6) = 6 birim.
Şimdi \vec{H} vektörünün x ve y bileşenlerini bulalım:
|\vec{H_x}| = |\vec{H}|cos143^\circKosinüs için trigonometrik dönüşüm yapalım, bildiğimiz bir açıyla uğraşalım.
cos143^\circ = -cos(180^\circ-143^\circ) = -cos37^\circ |\vec{H_x}| = -|\vec{H}|cos37^\circ|\vec{H_x}| = -20(0,8) = -16 birim.
Eksi işaretine dikkat edin.
|\vec{H_y}| = |\vec{H}|sin143^\circSinüs için trigonometrik dönüşüm yapalım, bildiğimiz bir açıyla uğraşalım.
sin143^\circ = sin(180^\circ-143^\circ) = sin37^\circ |\vec{H_y}| = -|\vec{H}|sin37^\circ|\vec{H_y}| = 20(0,6) = 12 birim.
Vektörlerin Bileşenlerine Ayrılması ile Bileşke vektörü bulmak
\vec{A} ve \vec{B} vektörlerinin uç uca ekleme ve paralel kenar yöntemleriyle bulunabileceğini biliyoruz. Bileşenlerine ayrırarak toplama yöntemi de şöyle:
Toplanacak olan vektörlerin bileşenleri:
\vec{A} = \vec{A_x} + \vec{A_y}
\vec{B} = \vec{B_x} + \vec{B_y}
Bileşke vektör iki vektörün toplamına eşit:
\vec{R} = \vec{A} + \vec{B}
Bileşke vektörü kendi bileşenleri cinsinden yazabiliriz:
\vec{R} = \vec{R_x} + \vec{R_y}
Bileşke vektörün x bileşeni toplanan vektörlerin x bileşenlerinin toplamına eşit:
\vec{R_x} = \vec{A_x} + \vec{B_x}
Bileşke vektörün y bileşeni de toplanan vektörlerin y bileşenlerinin toplamına eşit:
\vec{R_y} = \vec{A_y} + \vec{B_y}
Bileşke vektörün büyüklüğü:
R^2 = R_x^2 + R_y^2R^2 = (A_x+B_x)^2 + (A_y+B_y)^2
R = \sqrt{ (A_x+B_x)^2 + (A_y+B_y)^2}
Bileşenlerine ayırma yöntemiyle toplama en garantili yöntemdir, yeter ki matematikte dikkatli olun.
Örnek soru 2: Dört vektörün bileşkesi
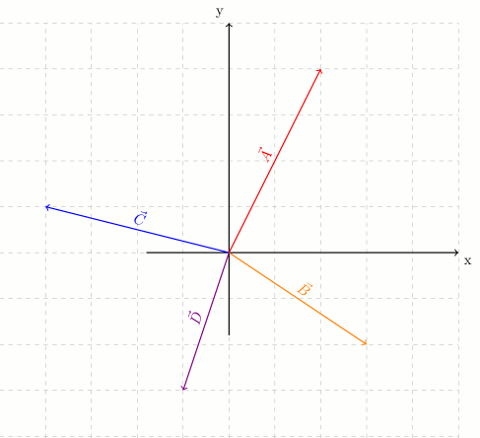
Yukarıdaki şekilde gösterilen \vec{A}, \vec{B}, \vec{C} \space ve \space \vec{D} vektörlerinin bileşkesi nedir?
Çözüm:
Şekil karışık görünüyor olabilir. Ama her vektörü bileşenlerine ayırırsak çok basitleşecek işimiz. Aşağıdaki şekil vektörlerin bileşenlerine ayrılmış halini gösteriyor.
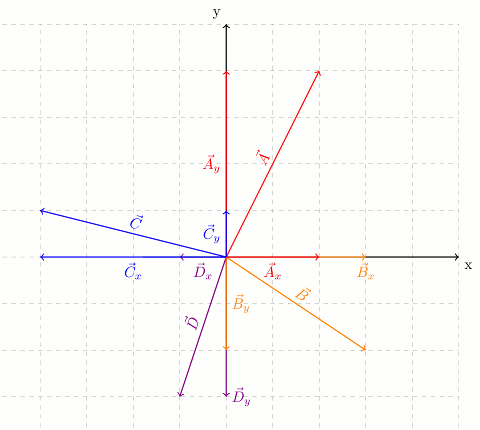
Tüm vektörlerin x bileşenleri aynı doğrultuda olduğu için şiddetlerini toplayabiliriz.
\vec{R_x} = \vec{A_x} + \vec{B_x} + \vec{C_x} + \vec{D_x}
x bileşenlerinin kaç kare olduğunu sayıyoruz. Örneğin, \vec{A_x} = 2.
Bileşenleri bulurken artı veya eksi işaretli olduklarına dikkat etmeliyiz. Sola doğru olanlan eksi işaretli. Örneğin, \vec{C_x} = -4 olduğuna dikkat edin.
\vec{R_x} = 2+3+(-4)+(-1)=0
Benzer şekilde y bileşenleri de aynı doğrultuda, büyüklüklerini toplayabiliriz.
\vec{R_y} = \vec{A_y} + \vec{B_y} + \vec{C_y} + \vec{D_y}
Bu kez y bileşenlerinin kaç kare olduğunu sayıyoruz. Yine negatif işaretlere dikkat etmeliyiz. Aşağı doğru olanlar eksi işaretli.
\vec{R_y} = 4+(-2)+1+(-3)=0
Tüm vektörler birbirini götürmüş, bileşke vektörümüz sıfır.
Örnek soru 3: Uzunluk ve açı bilindiğinde
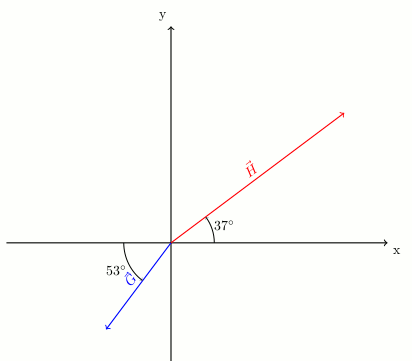
Yukarıdaki şekilde gösterilen \vec{G} vektörünün uzunluğu 5 birim, \vec{H} vektörünün uzunluğu 10 birim olduğuna göre, bu iki vektörün bileşkesinin uzunluğu kaç birimdir? (cos37^\circ = sin53^\circ=0,8 \space ve \space sin37^\circ = cos53^\circ=0,6 alınız.)
Çözüm:
Kare sayamıyoruz, o zaman hesaplama yapacağız. Bileşke vektörün bileşenlerini nasıl bulacağımızı biliyoruz:
R^2 = R_x^2 + R_y^2 R^2 = (G_x+H_x)^2 + (G_y+H_y)^2 R=\sqrt{(G_x+H_x)^2 + (G_y+H_y)^2}Yapmamız gereken iki vektörün bileşenlerindeki işaretlere dikkat etmek.
G_x = -Gcos53^\circ = -5(0,6) = -3 birim. Eksi işaretine dikkat, bu bileşen sola doğru.
G_y = -Gsin53^\circ = -5(0,8) = -4 birim. Eksi işaretine dikkat, bu bileşen aşağı doğru.
H_x = Hcos37^\circ = 10(0,8) = 8 birim. Artı işaretine dikkat, bu bileşen sağa doğru.
H_y = Hsin37^\circ = 10(0,6) = 6 birim. Artı işaretine dikkat, bu bileşen yukarı doğru.
Şimdi hesaplamayı tamamlayalım:
R = \sqrt{ (-3+8)^2 + (-4+6)^2}
R=\sqrt{29} = 5,39 birim. Her zaman tam sayılar denk gelmeyebilir.
Örnek soru 4: Eğik düzlemde vektörü bileşenlerine ayırma
Fizik dersinde özellikle kuvvet ve hareket konularında en sık karşılaşılan durumlardan biri eğik düzlem olacak. Eğik düzlemde bir cismin ağırlığını analiz etmeniz gerekecek. Aşağıdaki şekil bir eğik düzlemin üzerinde duran bir cismin ağırlık vektörünün bileşenlerine nasıl ayrıldığını gösteriyor.
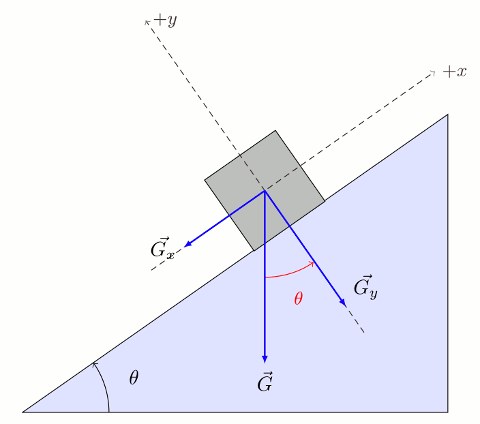
Eğik düzleme paralel ve dik olan eksenlere ihtiyacımız olacak. Normalde sol – sağ doğrultusunu gösteren x ekseni ve yukarı – aşağı doğrultusunu gösteren y eksenini döndürmemiz gerekecek. Döndürülen x ekseni eğik düzleme paralel, y ekseni dik olacak. Koordinat sistemimizi \theta açısı (yani eğik düzlemin yerle yaptığı açı) kadar döndürünce yeni koordinat sistemine erişmiş oluyoruz.
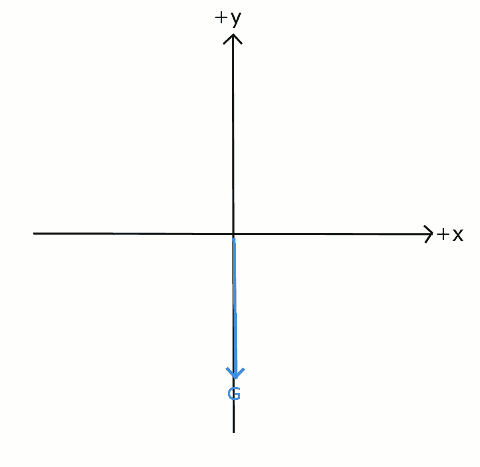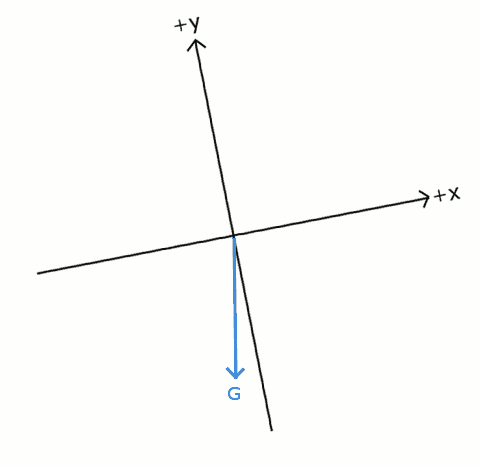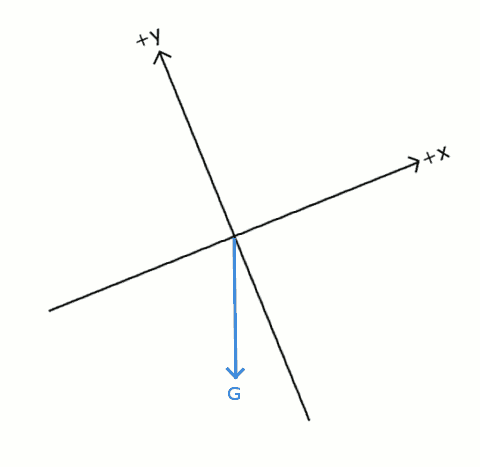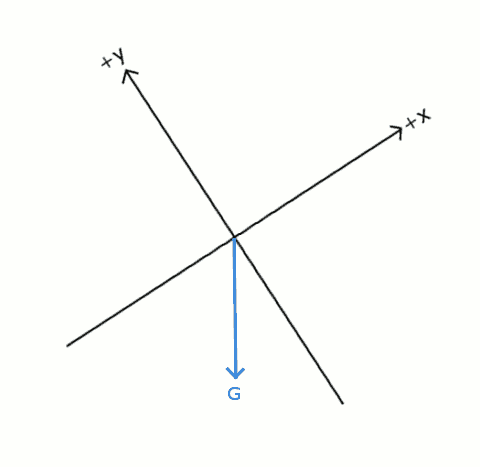
Yukarıdaki resimde görüldüğü gibi koordinat sisteminin döndürülmesi kuvvet vektörünü değiştirmiyor. Cismin ağırlık vektörünün yönü değişmiyor, hala yere dik doğrultuda aşağı doğru. Ağırlık vektörünün döndürülmüş koordinat sistemindeki bileşenlerini bulmak için, eksenlerle yaptığı açıları bilmemiz gerekiyor.
Dik üçgenlerdeki açı bağıntılarından G’nin y ekseniyle yaptığı açının \theta yani eğik düzlemin yerle yaptığı açıya eşit olduğunu görebilirsiniz.
- G vektörünü uzatıp eğik düzlemin tabanına kadar indirirseniz dik üçgen elde edersiniz.
- G ile eğik düzlemin yaptığı açının 90-\theta olduğunu fark etmelisiniz.
- Gx vektörünün eğik düzleme paralel olduğunu görüp, G ile Gx arasındaki açının da 90-\theta olduğunu fark etmelisiniz.
- Gx ve Gy birbirine dik olduğuna göre aralarındaki açı 90^\circ olmalı.
- Öyleyse G ile Gy arasındaki açı 90^\circ-(90^\circ-\theta = \theta)olmak zorunda.
Buradan sonrası kolay:
G_x = Gsin\theta = mgsin\theta G_y = Gcos\theta = mgcos\thetaVektörlerin Bileşenlerine Ayrılması ile ilgili Simülasyon
Vektörlerin bileşenlerine ayrılması yöntemiyle vektör toplama ve çıkarma işlemlerini görselleştiren şu simülasyon ilginizi çekebilir: Vektör Toplama PHET Simülasyonu
Vektörlerin Bileşenlerine Ayrılması ile ilgili Fizik Dersi Kazanımları
11.1.1.4. Bir vektörün iki boyutlu kartezyen koordinat sisteminde bileşenlerini çizerek büyüklüklerini hesaplar.
çok teşekkür ederim hele şu sondaki eğik düzlemdeki ağırlığın bileşenlerini bulmak için yazıdığınız yazı çok işime yaradı sebebini merak ediyordum teşekkürler .
Çok teşekkür ederim, gayet güzel ve anlaşılır, yalnız küçük bir hata var, ikinci Gy olmalı, yanlışlıkla Gx yazılmış.
Gx= G sinθ=mgsinθ Gy = Gcosθ= mgcosθ
Dikkatiniz harika! Düzeltildi.