Vida nedir? Örnek Sorular ve Çözümleri

Vidaları görmeyen yoktur. Duvara birşeyi asarken, mobilyaları birleştirirken bunları kullanırız. Ama vidanın nasıl çalıştığını hiç düşündünüz mü? Bir de tuhaf bir tanım yapalım. Vida bir eğik düzlemin bir silindire ya da koniye sarılmasıyla elde edilen bir basit makinedir. Silindir ve koni tamam da, eğik düzlem ne alaka diye düşünüyorsanız, vida adımlarına aşağıdaki şekilde kesiti verilen vidada bakmanızı öneririm.

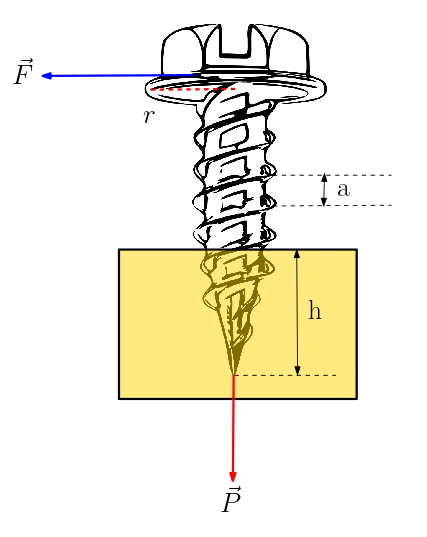
Vidayı tornavidayla döndürürüz. Döndürmek için uyguladığımız kuvveti F ile gösterdik (mavi ok). Vidanın tepesinin yarıçapı r (kırmızı kesikli çizgi). Vida adımı, yani ardışık iki diş arasındaki uzaklık, a ile gösteriliyor. Vida bir tam tur döndüğünde zeminde bir vida adımı kadar yer değiştirir. Vidanın zemine ne kadar derinlikle girdiğini de h ile gösterdik. n tur döndürülürse zeminde ilerleme miktarı yani derinliği h = na olur.

Eğer bir vidayı sıkıştırdıysanız, vidayı sadece döndürmenin yeterli olmadığını da hissetmiş olmalısınız. Döndürürken bir de bastırırsınız. Yani vida ilerlerken zemine P büyüklüğünde bir kuvvet uygular bunu da kırmızı okla gösterdik. Ayrıca zemin de vidaya tepki olarak aynı büyüklükte bir R tepki kuvveti uygular (Newton’un üçüncü yasasını hatırlayın).

Enerjinin korunumu kanununa göre F kuvvetinin vidayı bir tur döndürmek için yaptığı iş, vidanın tepki kuvvetine karşı zeminde bir adım ilerlemesi için gerekli enerjiye eşittir. Öyleyse:
F (2\pi r) = Pa

\frac{P}{F} = \frac{2\pi r}{a}

Bu sonucu yorumlayalım: Kuvvetten kazanç sağlanabilmesi (mekanik avantaj) için vida başının yarıçapının büyük, vida adımının küçük olması gerekir.

Örnek soru 1

Yarıçapı 5 mm olan bir vida F büyüklüğünde kuvvet ile 6 tur çevirildiğinde bir tahta blok içerisinde 2 cm ilerlemektedir. Buna göre tahtanın vidaya uyguladığı tepki kuvveti kaç F olur?

Çözüm

Az önce öneli bir sonuca ulaşmıştık. P ile F arasındaki ilişkiydi bu.
\frac{P}{F} = \frac{2\pi r}{a}

Tek yapmamız gereken vida formülünde bildiklerimizi yerleştirmek. Formülleri ezberlemeyin, çıkarmayı öğrenin bu arada.

Önce vida adımını bulalım. Vida 6 tur çevrilince 2 cm ilerliyorsa, bir turda kaç cm ilerler?
h = na

2cm = 6a a = \frac{2 \space cm}{6} = \frac{1}{3} \space cm

Şimdi yerine koyalım:
\frac{P}{F} = \frac{2\pi (5 \times 10^{-3}m)}{ \frac{1}{3}\times 10^{-2}m}

\frac{P}{F} = 2\pi \times 3 \times 5 \times 10^{-1} = 3\pi P = 3\pi F

Örnek soru 2

Yarıçapı 1 cm olan bir vida 50 N büyüklüğündeki kuvvetle döndürüldüğünde vidanın ucu zemine 1200 N büyüklüğünde bir kuvvet uygulamaktadır. Vida adımı 1 mm ise bu vidanın verimi kaçtır? (π = 3 alabilirsiniz).

Çözüm

Vida bir tam tur döndüğünde bulunduğu zeminde bir vida adımı (a) ilerler. Verim formülünü yazalım.
Verim = \frac{Alınan \space enerji}{Verilen \space enerji}

O zaman alınan ve verilen enerjileri hesaplamalıyız.

Alınan enerji için W_Alınan = Pa olduğunu biliyoruz, yani P kuvvetinin bir vida adımında yaptığı iş.
W_{Alınan} = 1200 \space N \times 1 \times 10^{-3} \space m = 1,2 \space J

Verilen enerji de vidayı döndürdüğümüz kuvvetle vidanın başının bir tur attığında yaptığı iş: W_verilen = F (2πr)
W_{verilen} = 50 \space N \times 2 \pi \times 1 \times 10^{-2} \space m = \pi \space J = 3 \space J

Verimi bulalım:
Verim = \frac{1.2}{3} = 0,4 = \% 40

Vidalarla ilgili Kazanımlar

11.1.10.1. Günlük hayatta kullanılan basit makinelerin işlevlerini açıklar.

• Kaldıraç, sabit ve hareketli makara, palanga, eğik düzlem, vida, çıkrık, çark ve kasnak ile sınırlı kalınır.

11.1.10.2. Basit makineler ile ilgili hesaplamalar yapar.

• İkiden fazla basit makinenin bir arada olduğu sistemlerle ilgili matematiksel hesaplamalara girilmez.
• Hesaplamaların günlük hayatta kullanılan basit makine örnekleri (anahtar gibi) üzerinden yapılması sağlanır.
• Basit makinelerde verim ile ilgili matematiksel hesaplamalar yapılması sağlanır.