Yer değiştirme nedir?
Yer değiştirme hareket eden bir cismin ilk konumuyla son konumu arasındaki farka denir. Konum vektörlerinin farkı olduğu için yer değiştirme de vektördür, hem büyüklüğü hem de yönü vardır. Konum farkını gösterdiği için ∆x sembolüyle gösterilir. Yer değiştirme artı, eksi ya da sıfır olabilir. Matematiksel olarak şöyle ifade edilir:
\Delta\vec{x} = \vec{x}_{son} - \vec{x}_{ilk}Alınan yol nedir?
Alınan yol ise bir cismin hareketi boyunca izlediği yörüngenin toplam uzunluğudur. Alınan yol d sembolüyle gösterilir, vektörel değil skaler bir büyüklüktür, yönü yoktur ve asla eksi işaretli olamaz. Alınan yol yer değiştirmeye ya eşittir ya da daha büyüktür. Alınan yolun belli bir formülü yoktur, yolun uzunluğu ya ölçülür ya da daha küçük parçalardan oluşuyorsa parçaları toplanır.
Yer değiştirmenin de alınan yolun da birimi metredir.
Bu kavramları daha iyi anlamak için bir kaç örnek soruya bakalım:
Örnek Soru 1 – Bir boyutta yer değiştirme ve alınan yol
Şekildeki K kutusu doğrusal bir yolun 0 noktasından başlayarak önce sağa doğru 4 m, sonra da sola doğru 3 m gitmiştir. K kutusunun yer değiştirme vektörünün uzunluğu ve aldığı yol kaç metredir?
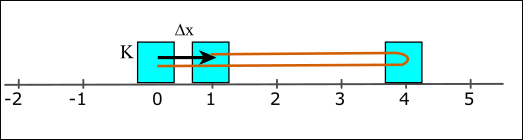
Çözüm:
Yer değiştirmenin tanımını hatırlayalım:
\Delta\vec{x} = \vec{x}_{son} - \vec{x}_{ilk}Yer değiştirme için önemli olan tek şey ilk ve son konumdur, yörüngenin önemi yoktur. Bu durumda ilk konum vektörü 0, son konum vektörü ise +1 m’dir. Öyleyse,
\Delta\vec{x} = 1 - 0 = +1 \space mAlınan yol, yörüngenin uzunluğudur. Yani kutunun giderken aldığı yolla dönerken aldığı yolun toplamıdır. Bu durumda,
d = 4 \space m + 3 \space m = 7 \space mBu soruda yer değiştirme sağa doğru 1 m iken, alınan yol 7 m olarak bulunmuştur.
Örnek Soru 2 – Eksi yer değiştirme
Şekildeki A kutusu 0 noktasından başlayıp önce 4 m sağa gitmiş sonra yön değiştirip 6 m sola hareket etmiştir. Kutunun yer değiştirmesi ve aldığı yol nedir?
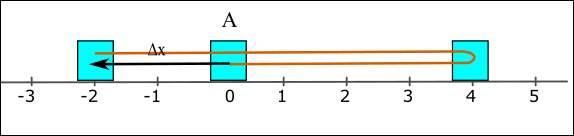
Yer değiştirme vektörünü bulmak için tek ihtiyacımız olan ilk ve son konum vektörlerini bilmemizdir. Bu soruda ilk konum vektörü 0 m’dir. Son konum vektörü ise xson = -2 m’dir. Öyleyse,
\Delta{x} = -2 \space m - 0 \space m = -2 \space mYer değiştirmenin değeri eksi olabilir, bu yer değiştirmenin sola doğru olduğunu gösterir.
A kutusunun yörüngesi şekilde turuncu çizgiyle gösterilmiştir, alınan yol bu çizginin uzunluğudur. Hareketinin iki kısımdan oluştuğunu bildiğimiz için alınan yolu bulmak için bu parçaları toplarız:
Örnek Soru 3 – İki boyutta yer değiştirme ve alınan yol
Şekildeki kutu başlangıç noktasından önce doğuya doğru 3 m, sonra kuzeye doğru 4 m gitmiştir. Kutunun yer değiştirme vektörünü çizip büyüklüğünü hesaplayın ve aldığı yolu bulun.
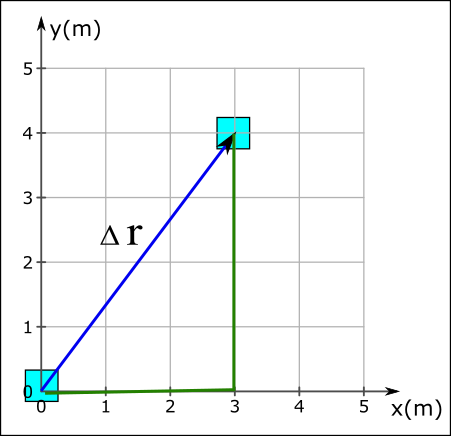
Çözüm:
Kutunun yer değiştirmesini bulmak için yalnızca başlangıç ve bitiş konumlarını bilmemiz yeterlidir. Başlangıç konumu:
\vec{r}_{ilk} = 0Bitiş konumu:
\vec{r}_{son} = (3 m, 4m)Öyleyse yer değiştirme vektörü Δr şekilde gösterilen mavi oktur. Bu vektörün uzunluğunu Pisagor teoreminden bulabiliriz:
|\Delta\vec{r}|^2 = 3^2 + 4^2 = 9 + 16 = 25 |\Delta\vec{r}| = \sqrt{25} = 5 \space mAlınan yol ise şekilde yeşille gösterilen iki doğru parçasından oluşmaktadır.
d = 3 \space m + 4 \space m =7 \space mGördüğünüz gibi bu örnekte alınan yol, yer değiştirmeden daha fazladır.
Örnek Soru 4 – Başladığı konuma dönme
Bir koşucu yarı çapı 50 m olan dairesel bir yolda bir tam tur atmıştır. Koşucunun yer değiştirmesi ve aldığı yol nedir?
Çözüm:
Koşucu bir tam tur attığına göre başlangıç konumuyla bitiş konumu aynı demektir. Öyleyse yer değiştirmesi sıfırdır.
Koşucunun aldığı yol, izlediği yörüngenin uzunluğuna yani çemberin çevresine eşittir.
d = 2\pi{r} = 2\times3,14\times50m = 314 \space mYer Değiştirme ve Alınan Yol Problemleri
1. Bir tekne doğrusal bir rotada önce kuzeye 18 km, sonra güneye 27 km gidiyor. Teknenin harekete başladığı noktaya göre yer değiştirmesi ve aldığı yol ne kadardır?
2. Labirentteki bir fare önce 3 m sağa, ardından 6 m yukarı, sonra 5 m sağa doğru ilerliyor. Farenin yer değiştirme vektörünü çizip büyüklüğünü bulun, aldığı yolu hesaplayın.
Yer değiştirme ve Alınan Yol ile ilgili Kazanımlar
9.3.1.3. Konum, alınan yol, yer değiştirme, sürat ve hız kavramlarını birbirleri ile ilişkilendirir.
Gerçekten çok güzel bir sayfa.Sınava çok iyi hazırlıyor 🙂
Beğenmene sevindim. Ama sadece sınav olarak düşünme derim. İlginç şeyler bence bunlar.
Evet gerçekten güzel artı olarak kısa ve öz bilgiler olduğu için slayt hazırlarken bu bilgileri kullanıyorum içtenlikle teşekkür ediyorum.
ya gerçektende tesekür ederim işime yaradı
hoş bi sayfa. 🙂
Fizik kitabı,test kitabı ve defter o kadar karmaşık ve boş yazışmışki burası lütuf gibi
Hoş bir sayfa
Gerçekten iyi anlatılabilmek için her şey denenmiş çok güzel bir sayfa Teşekkürler
Çok teşekkürler çok isine yaradı harikasınız…
Örnek 2’de 6 m sola hareket etmiştir. Düzeltebilir misiniz?
Düzeltildi. Teşekkürler.
Havaya attığımız bir cisim dünya döndüğü halde, bir süre sonra nasil aynı noktaya düşer? Ya da şöyle sorayim diyelim elimde bir füze var ve benim konumum a, 10 dk lık bir uçuş sonrası b noktasına düşmesini istiyorum ama bu esnada da dünya dönüyor ve çeşitli hava olayları yaşanıyor, bu füze tüm bu olaylardan sıyrılıp nasıl 10 dk sonra b noktasına ulaşır?
cevabı eylemsizlik ilkesi bir cisim belli bi yönde hareket ediyosa aksi bir kuvvet etmediği sürece aynı hızda aynı yönde ilerlemeye devam eder mesela sen arabayla giderken araba bi anda fren yaptığında senin ileriye doğru çekiliyo gibi olmanın sebebi de odur sen aksi yöndeki kuvvet hızını sıfırlayana kadar mevcut hareketini korursun özetle dünya belli bi hızla dönerken cisim de o hızla döner sen onu havaya attığında cisim de dünyayla beraber dönmeye devam eder nasıl dünyadan kopmuyo diceksen de bu da yer çekimi kuvvetidir füzenin rüzgardan etkilenmemesinin nedeni sürtünme kuvvetinin onu çok az yavaşlatması ve zaten bu hesaplamalar yapılarak füzenin atılmasıdır
keşke pdf de yapsaydınız
Çok güzel ve basit bir anlatım olmuş teşekürler.Üstelik koyduğun sorular konuyu anlama sürecindeki birisi için çok iyi…
Yer değiştirmeyi o kadar karmaşık anlatmışlar ki Pisagor bağıntısı falan bu sayfa çok iyi
Gerçekten harika bir sayfa
merhaba, koşucu sorusunda kafam karıştı, 14 nereden geldi? direkt dairenin çevresini 6 x 50’den bulmuyor muyuz?
π = 3 alırsak evet 2 x 3 x 50, ama π=3,14 alıyoruz.