Daha önce, 9. sınıfta, fizikte iş ne demek öğrenmiştiniz, tekrar okumanızı öneririm. Bu yazıda yapılan işi hesaplamak için kuvvet – konum (ya da kuvvet – yol) grafiklerini nasıl kullanacağınızı öğreneceksiniz.
İş ne demektir?
Hatırlatmak için işin tanımını tekrar verelim. Fizikte iş, enerji aktarmanın bir yoludur. Fiziksel iş yapılabilmesi için cisme uygulanan kuvvetin bir bileşeninin cismin yerdeğiştirmesi ile aynı doğrultuda olması gerekir. Kuvvetin bir bileşenin yerdeğiştirmeye paralel olması ne demek bir örnekle gösterelim. Aşağıdaki resimde ilk başta duran bir kutuyu belli bir açı yapacak şekilde çekiyoruz. Sürtünmeyi ihmal ediyoruz. Kutu ilk konumundan ikinci konumuna ilerliyor yani Δx kadar yer değiştiriyor. Yerdeğiştirmenin bir vektör olduğunu da hatırlayın. Kutu neden yerdeğiştirdi, dururken harekete geçti? Çektiğimiz için. Yani uyguladığımız kuvvet yerdeğiştirmenin sebebi, çekmeseydik kutu olduğu yerde durmaya devam edecekti.
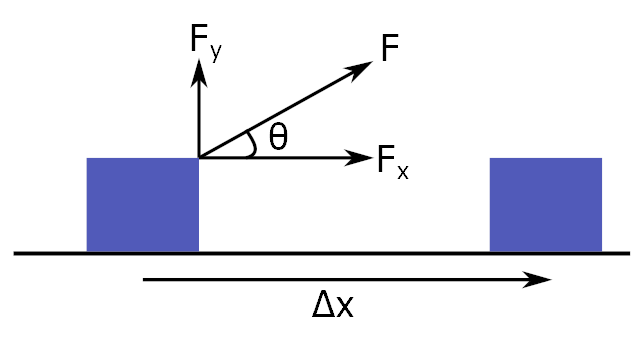
Artık tanımı verebiliriz. Kuvvetin yaptığı iş:
W = \vec{F}cos\theta \vec{\Delta x}
cosθ nereden çıktı? Kuvvetin yerdeğiştirmeye paralel olan bileşeni Fx = Fcosθ olduğu için sadece x bileşeni iş yapıyor. Fy = Fsinθ yerdeğiştirmeye dik olduğu için iş yapmıyor. Buradan iki çıkarımda bulunabiliriz:
- θ = 90° için cos90° = 0 öyleyse W = 0, kuvvet yerdeğiştirmeye dik ise iş yapılmaz.
- θ = 0° için cos0° = 1 öyleyse W = FΔx, kuvvet yerdeğiştirmeye paralel ve aynı yönlü ise pozitif iş yapılır.
- θ = 180° için cos180° = -1 öyleyse W = -FΔx, kuvvet yerdeğiştirmeye paralel ve zıt yönlü ise negatif iş yapılır.
Kuvvet – Konum Grafikleri
Kuvvet – konum grafiğinin altında kalan alan yapılan işi verir. Bunu bir örnekle inceleyelim. Aşağıdaki grafik bir kutuya x ekseni doğrultusunda uygulanan kuvvetin konuma göre değişimini gösteriyor.
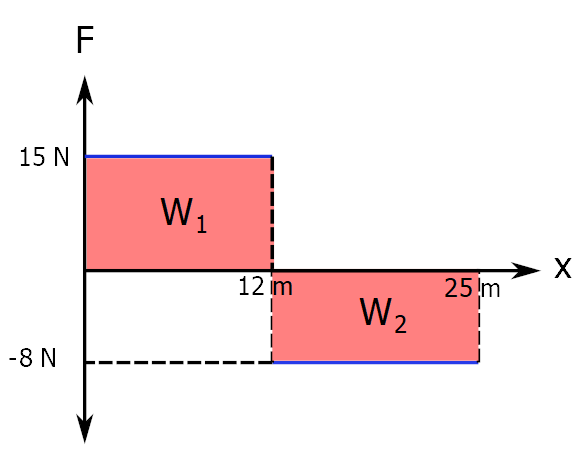
Önce bu grafik bize ne anlatıyor yorumlayalım. Önümüzde bir cisim var, sürtünmesiz düz bir yolda duruyor. Bu cismi önce 12 metre 15 Newton kuvvetle sağa doğru (+x yönünde) çekmişiz ya da itmişiz. Sonra 12 metreden 25 metreye kadar cismi sola doğru (-x yönünde) 8 Newton kuvvetle çekmişiz ya da itmişiz. Yani 12. metrede cisme uyguladığımız kuvvetin yönünü tam zıt olacak şekilde değiştirmişiz.
Şimdi iş hesaplayalım. İş bu grafiğin altında kalan alan demiştik. Şimdi altında kalan alan ne demek onu netleştirelim. Grafiğe tekrar bakın, pembe bölgeler, bu durumda dikdörtgen bölgeleri kastediyoruz. Yani toplam iş:
W = W1 + W2
X ekseninin üstünde kalan W1 bölgesinde yapılan işin pozitif, x ekseninin altında kalan W2 bölgesinde yapılan işin negatif olduğunu görüyoruz. Hesaplarsak:
W1 = 15 x 12 = 180 Nm = 180 J
W2 = -8 x (25-12) = -8 x 13 = -104 Nm = -104 J
W = 180 J + (-104 J) = 76 J
Sayıları yerine koyarken kuvvetin yönündeki eksi işaretine dikkat ederseniz toplam işi bulmanız kolay. Ama işarete dikkat etmeden sadece eksenin üstüne artı altına eksi iş değerlerini yazarsanız da toplam işi bulabilirsiniz.
Örnek soru
Sürtünmesiz yatay düzlemde duran bir cisim aşağıdaki kuvvet – konum grafiğine göre kuvvet uygulanarak hareket ettirilmiştir. Buna göre cismin üzerinde yapılan iş kaç joule’dur?
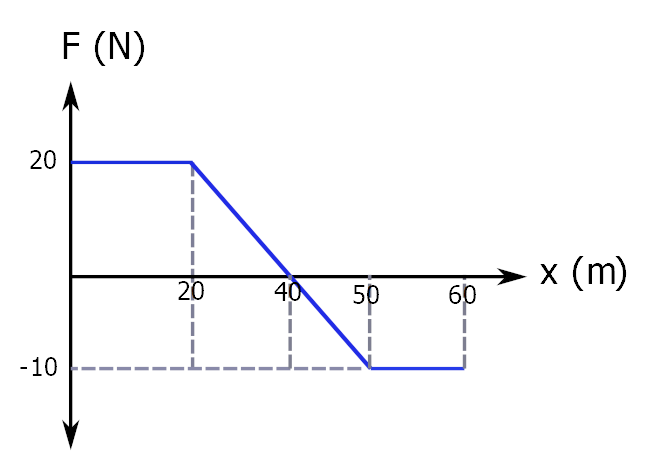
Çözüm
Bir önceki örnekte yaptığımızın aynısını yapacağız. x ekseninin üstünde kalan kısım pozitif iş, altında kalan kısım negatif iş. Ayrı ayrı hesaplayıp sonra birleştireceğiz.
İlk önce sol üstteki kısmı hesaplayalım. Dikkat ederseniz bu bir yamuk. Yamuğun alanını nasıl hesaplıyorduk:
Alan = \frac{alt \space taban + ust \space taban}{2} \times yukseklik
W1 = ((40 m + 20 m)/2) x 20 N = 600 J (pozitif olduğuna dikkat edin.)
Alttaki kısmı adım adım yapalım kafamız karışmasın.
Alt taban = 60 m – 40 m = 20 m
Üst taban = 60 m – 50 m = 10 m
Yükseklik = -10 N.
W2 = ((20 m+10 m)/2) x -10 N = -150 N (negatif olduğuna dikkat edin.)
Şimdi yapılan toplam işi bulabiliriz:
W = W1 + W2
W = 600 J + (-150 J) = 450 J
Kuvvet – konum grafikleri ile ilgili kazanımlar
2018 – 11.1.6.1. Yapılan iş ile enerji arasındaki ilişkiyi analiz eder.
- Kuvvet-yol grafiğinden faydalanılarak iş hesaplamaları yapılır.
- Matematiksel hesaplamalar yapılması sağlanır.