İtme nedir? İtme ve momentum ilişkisi nasıldır?

Duran bir kutuya kuvvet uyguladığınızı düşünün, kutuyu itiyor olun. Ne kadar çok kuvvet uygularsanız ve ne kadar uzun süre iterseniz kutu o kadar hızlanmaz mı? Fizikteki itme kavramı bu ilişkiyi anlatır. İtmenin formülü (tanımı ya da matematiksel modeli) kuvvet ile kuvvetin uygulanma süresinin çarpımıdır. İtme vektörel bir büyüklüktür, çünkü kuvvet vektöreldir. İtmenin yönü her zaman kuvvet vektörünün yönüyle aynıdır. İtme I simgesiyle gösterilir ve SI birimi Ns (Newton saniye)’dir. Ayrıca itme bir türetilmiş büyüklüktür. İtmenin formülünü bir de vektörel biçimiyle görelim:
\vec{I} = \vec{F}\Delta t

İtme ve momentum arasındaki ilişki

Newton’un hareket kanunlarını hatırlayalım. Newton’un ikinci kanunu bize bir cisme kuvvet uyguladığımızda cisme bir ivme kazandıracağımızı söylüyor. Artık çizgisel momentum ve itme kavramlarını da bildiğimize göre bu kanunu daha derinlemesine anlayabiliriz. Önce ikinci kanunu yazalım sonra adım adım ilerleyelim.
\vec{F} = m\vec{a}
İvmenin tanımının hız değişiminin zaman değişimine oranı olduğunu biliyoruz.
\vec{a} = \frac{\vec{\Delta v}}{\Delta t}
İvme yerine bunu yazalım.
\vec{F} = m\frac{\vec{\Delta v}}{\Delta t}
Şimdi bu denklemi düzenleyelim.

\vec{F}\Delta t = m\vec{\Delta v} = \Delta \vec{p}

Momentum değişiminin itmeye eşit olduğu sonucuna vardık. Şimdi günlük yaşamdaki deneyimimizle bu sonucu yorumlayalım. Bir cisme ne kadar uzun süre kuvvet uygularsak momentumunu o kadar artırırız. Gayet mantıklı görünüyor. Son olarak Newton’un ikinci kanunun asıl halini görelim.
\vec{F} = \frac{m\vec{\Delta v}}{\Delta t} = \frac{\Delta \vec{p}}{\Delta t}
Bu haliyle Newton’un ikinci yasası bize uygulanan kuvvetin birim zamandaki momentum değişimine eşit olduğunu söylüyor. Kuvvet uygulamak bir cismin momentumunun değişmesine sebep oluyor. Momentum değişiminin yönü (evet yönü var çünkü momentum bir vektör) uygulanan kuvvetle aynı yönde. Bu kavramı pekiştirmek için bir örnek soru çözelim.

Örnek soru 1

Şekilde gösterilen sürtünmesiz yatay düzlemde başlangıçta hareketsiz olan, 2 kg kütleli bir cisime 3 saniye boyunca 10 N büyüklüğünde sabit kuvvet uygulanıyor. Buna göre 3. saniyenin sonunda cismin hızı kaç m/s olur?

Çözüm

Aslnda bu soruyu Newton’un ikinci yasasındaki ivmeyi kullanarak çözebiliriz. Ama amacımız zaten Newton’un ikinci yasasının momentumun değişimi cinsinden ifade edilebildiğini sınamak. Önce hesaplayalım:

İtmeyi momentum değişimine eşitleyelim.
\vec{F}{\Delta t}=m\Delta \vec{v}

10(3) = 2\Delta \vec{v} \Delta \vec{v} = \frac{30}{2} = 15 m/s

İlk hız sıfır olduğu için hız değişimi son hıza eşit, yani son hızımızın büyüklüğü 15 m/s.

Şimdi ivmeyle çözüp doğru mu bu sonuç kontrol edelim.
\vec{F} = m\vec{a}

10 = 2\vec{a} \vec{a} = \frac{10}{2} = 5 m/s^2

Şimdi son hızı hesaplayalım.
\vec{v} = \vec{a}\Delta t

\vec{v} = 5(3) = 15 m/s

Gördüğünüz gibi aynı sonuca ulaştık ama daha az işlem yapmamız gerekti.

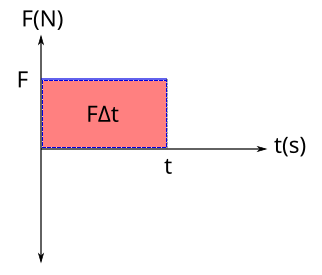
Kuvvet – zaman grafikleri ve momentum

Sıklıkla karşılaşacağınız soru tipleri arasında itmeyi kuvvet – zaman grafiklerini kullanarak hesaplamak olacak. Aşağıdaki grafikte kuvvet – zaman grafiğinin altında kalanın itmeye ya da momentum değişimine eşit olduğunu görebiliyoruz.

Şimdi bir örnek çözelim.

Örnek soru 2

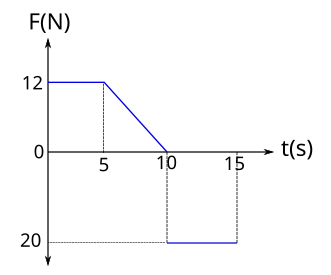
Sürtünmelerin ihmal edildiği yatay düzlemde bir cisme uygulanan kuvvetin zamana göre değişim grafiği şekilde verilmiştir. Buna göre cisme uygulanan itmenin büyüklüğü kaç Ns’dir?

Çözüm

Tüm itmeleri grafiğin altında kalan alandan hesaplayacağız. Sonra toplayacağız.

0 – 5 saniye arasında cisme sabit 12 N kuvvet uygulanmış.
\vec{I_1} = 12(5-0)=60 Ns
5 – 10 saniye arasında kuvvet doğrusal olarak azalmış. Bu bir dik üçgen, alanını hesaplayabiliriz.
\vec{I_2}=\frac{12(10-5)}{2} = 30 Ns
10 – 15 saniye arasında sabit 20 N kuvvet uygulanmış, ama yönü zıt, buna dikkat.
\vec{I_3} = -20(15-10)=-100 Ns
Toplam itmeyi artık bulabiliriz:
\vec{I} = 60 + 30 - 100 = -10 Ns
İtmenin büyüklüğü 10 Ns ama yönü eksi.

Momentum – zaman grafikleri

Bir başka soru tipi de momentumun zamana bağlı değişimini gösteren grafiklerle ilgili hesaplamaları ve yorumları içeriyor. Momentum zaman grafiğinin eğitimi uygulanan kuvveti verir. Çünkü eğim:
tan \alpha =\frac{\Delta\vec{P}}{\Delta t} = \frac{\vec{F}\Delta t}{\Delta t} = \vec{F}
Bunu da bir örnek çözerek görelim.

Örnek soru 3

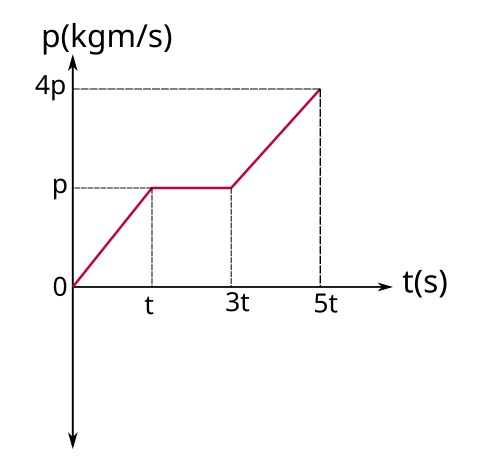
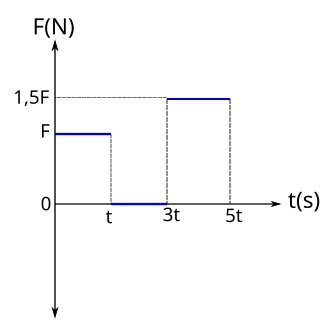
Sürtünmesiz yatay düzlemde hareket eden bir cisme ait momentumun zamana göre değişimini gösteren grafik şekildeki gibidir. Buna
göre cisme etki eden net kuvvetin zamanla değişim grafiğini çiziniz.

Çözüm

Zaman aralıkları için grafiğin eğimini hesaplayarak uygulanan kuvveti bulacağız.

0 – t aralığı için p/t = F₁ = F diyelim, yönümüz artı.

t – 3t aralığında eğim sıfır, momentum değişmemiş. Cisim sabit hızla gitmiş, dolayısıyla net kuvvet sıfır olmuş. F₂ = 0

3t – 5t aralığında momentum değişimi 4p – p = 3p, zaman değişimi 5- 3t = 2t. F₃ = 3p/2t, bunun 3F/2 yani 1,5 F olduğunu görebiliyoruz yönümüz hala artı. Artık grafiği çizebiliriz.

Örnek soru 4

Bir de kuvvet – zaman grafiğinden, momentum – zaman grafiği çizmeyi görelim. Örnek soru 2’deki kuvvetin zamana göre değişimini gösteren grafiği kullanarak cismin momentumunun zamana göre değişim grafiği nasıl çizilir?

Çözüm

Sırayla momentum değişimlerini hesaplayacağız. Bunu grafiğin altında kalan alanları hesaplayarak yapacağız.

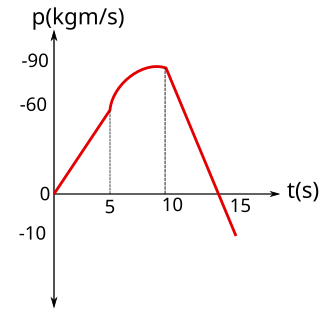
0 – 5s arasında sabit 12 N kuvvet uygulanmış. Momentum değişimini bulabiliriz. Momentum değişimi pozitif ve doğrusal.
\Delta \vec{p} = 12(5-0)=60 kgm/s
5 – 10 saniye arasında azalan bir kuvvet uygulanmış ama yönü artı, bu azalan bir parabol olacak çizerken. hala momentum değişimi pozitif.
\Delta \vec{p} = \frac{(12-0)(10-5)}{2}=30 kgm/s
t = 10 s için p = 60 + 30 = 90 kgm/s değerini elde ettik.

10 – 15 saniye arasında sabit ama eksi yönlü bir kuvvet uygulanmış. Momentum değişimi negatif olacak, ama doğrusal.
\Delta \vec{p} = (-20-0)(10-5)= -100 kgm/s
t = 15 s için p = 90 – 100 = -10 kgm/s değerini elde ettik. Artık momentum zaman grafiğini çizebiliriz.

İtme ve momentum ilişkisi ile ilgili kazanımlar

11.1.7.1. İtme ve çizgisel momentum kavramlarını açıklar.

• İtme ve çizgisel momentum kavramlarının matematiksel modeli verilir.

11.1.7.2. İtme ile çizgisel momentum değişimi arasında ilişki kurar.

• Öğrencilerin Newton’ın ikinci hareket yasasından faydalanarak itme ve momentum arasındaki matematiksel modeli elde etmeleri sağlanır.
• Öğrencilerin kuvvet-zaman grafiğinden alan hesaplamaları yapmaları ve cismin momentum değişikliği ile ilişkilendirmeleri sağlanır.
• İtme ve çizgisel momentum değişimi ile ilgili matematiksel hesaplamalar yapılması sağlanır.