Eylemsizlik momentini tanımlamadan önce eylemsizliği hatırlayalım, çünkü bu iki kavram yakından ilişkili. Eylemsizlik bir cismin hareket durumundaki değişikliğe karşı gösterdiği direnç olarak tanımlanır. Bir saniye durun ve düşünün hareket durumu ne demek, hareket durumundaki değişiklik ne demek? Hareket durumu bir cismin hızıdır (hızın vektörel olduğunu da hatırlayın). Hareket durumundaki değişiklik de hızın zamana göre değişmesi yani ivmedir. Bu durumda eylemsizlik dediğimiz cismin ivmelenmeye ne kadar direnç gösterdiği anlamına gelir, bunu da Newton’un hareket kanunlarından biliyoruz, bu kütle. Newton’un hareket kanunlarını daha önce incelediğimizde sadece öteleme hareketine bakmıştık. Peki dönme hareketinde Newton’un hareket yasaları nasıl bir hal alıyor? Bu soru bizi eylemsizlik momentini tanımlamaya götürecek.
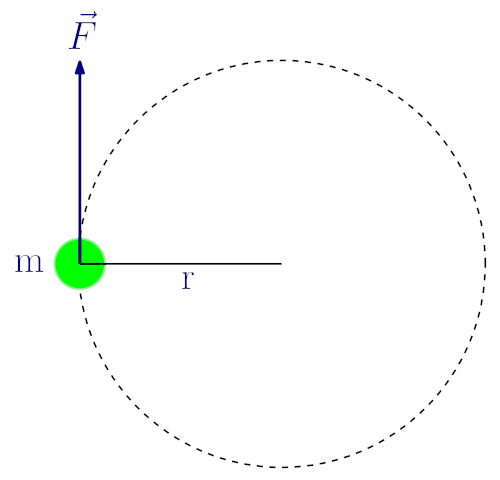
Yukarıdaki resimde m kütleli bir top r yarıçaplı bir yörüngede dairesel hareket yapıyor. Bu topa yörüngeye teğet bir F kuvveti uygulanıyor. Önemli soru şu: bu topun hareket durumu (yani hızı) nasıl değişir? Newton’un hareket kanunlarını ve çembersel hareket bilgilerimizi kullanarak inceleyelim.
\vec{F_T} = m\vec{aT}
Düzgün çembersel harekette çizgisel hız değişmiyordu bu nedenle açısal hızda bir değişim görmüyorduk. Ama çizgisel bir kuvvet uygularsak çizgisel hızımız da değişir.
\Delta \vec{v} = \vec{v_2} - \vec{v1}
Çizgisel hızla açısal hız arasındaki ilişkiyi hatırlayalım.
\vec{v} = \omega r
Dolayısıyla açısal hızımız da değişir.
\Delta \vec{v} = \omega_2 r - \omega1 r = r(\omega_2 - \omega1)
\frac{\Delta \vec{v}}{\Delta t} = r\frac{\Delta \omega}{\Delta t}
Bu durumda açısal ivme diye bir büyüklük tanımlayabiliriz. Bu açısal hızın zamana göre değişimi demek.
\alpha = \frac{\Delta \omega}{\Delta t}
Öyleyse çizgisel ivme ile açısal ivme arasındaki ilişki şöyle olur.
\vec{a_T} =r\alpha
Şimdi F = ma’da yerine yazabiliriz.
\vec{F_T} = m\vec{aT} = mr\alpha
Son numaramız dönme hareketiyle uğraştığımız için bu hareketle ilişkili bir büyüklük olan torka geçiş yapmak. Eşitliğin ikitarafını da r ile çarparsak torku buluruz.
F_T \times r = mr\alpha r
Çok uğraştık ama eylemsizlik momentinin formülünü bulduk.
I = mr^2
Şimdi bu formül ya da tanım ne anlama geliyor bunun üzerinde düşünelim. Bir katı cisme bir tork uygulayıp dönmeye zorladığımızda, yani hareket durumunu değiştirdiğimizde, bu değişikliğe karşı bir direnç gösteriyor. İşte bu dirence eylemsizlik momenti diyoruz. Yani dönen cisimlerin dönmeye karşı gösterdikleri direnç bu. Tıpkı eylemsizlik gibi. Öteleme hareketinde bu direnç kütleydi, dönme hareketinde ise eylemsizlik momenti.
Eylemsizlik momentinin toplanabilirliği
Eylemsizlik momentinin tanımını öğrendik, türetilmiş ve skaler bir büyüklük olduğunu da anlamış olmalısınız. İyi de bunu neden öğreniyoruz? Ne işimize yarayacak diye merak ediyor olabilirsiniz. Mühendislikte ve diğer bilimsel alanlarda sıklıkla kullanılıyor. Yukarıdaki örnekte tek bir parçacığa bakmıştık, şimdi katı cisimler için eylemsizlik momentini yorumlayalım.
Önce aşağıdaki resimde gösterilen gibi bir çubuk düşünelim. Bu çubuk katı, örgü şişi gibi birşey, ama o kadar hafif olsun ki kütlesini ihmal edelim. Sonra bu çubuğun farklı noktalarına oyun hamurlarını yerleştirelim. Sonra eylemsizlik momentlerini kıyaslayalım.
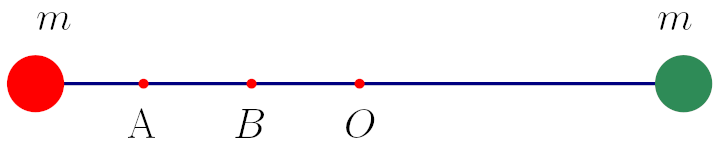
İlk sorum şu. Bu çubuğu hangi noktadan tutarsanız döndürmek en kolay olur. Bu eylemsizlik momentinin en küçük olduğu durum olmalı, çünkü torkun en az olduğu nokta eylemsizlik momentinin de en az olduğu noktada. O noktasının çubuğun tam ortası ve noktaların arasındaki mesafenin eşit olduğunu varsayalım. Bir ara bunu deneyebilirsiniz, bir çöp şiş iki üzüm yeter. Bu sistemi anlamak için ilk fark etmemiz gereken şey eylemsizlik momentinin toplanabilir bir büyüklük olduğu, tıpkı kütle gibi. Yani bu sistemin eylemsizlik momenti iki ucundaki kütlelerin ayrı ayrı eylemsizlik momentlerinin toplamına eşit.
Önce A noktasını ele alalım. Kırmızı kütle ile A arası uzaklık r olsun, AB ve BO arası da r. O noktasından yeşil kütleye olan mesafede r+r+r = 3r olur. Şimdi kütleleri ve uzaklıkları bildiğimize göre eylemsizlik momentlerini bulup sonra da kıyaslayabiliriz.
I_k = mr^2; I_y = m(6r-r)^2 = 25mr^2; I_A = I_k + I_y = mr^2(1+25) = 26mr^2
Şimdi B için yapalım:
Ik = m(2r)^2 = 4mr^2; I_y = m(4r)^2 = 16mr^2; IB = I_k + I_y = mr^2(4+16) = 20mr^2
Son olarak da O noktasına bakalım:
I_k = m(3r)^2 = 9mr^2; I_y = m(3r)^2 = 9mr^2; I_O = I_k + I_y = mr^2(9+9) = 18mr^2
Gördüğümüz gibi eylemsizlik momenti en az çubuğun tam ortasında çıktı.
Katı cisimlerin eylemsizlik momenti
Katı ve düzgün geometrik şekilli cisimlerin eylemsizlik momentini, cismi küçük parçacıklar gibi modelleyerek bulabiliriz. Ama integral işin içine gireceği için, 12. sınıf seviyesinde burada durmak isterim. Sadece sık kullanılan bazı katı cisimlerin merkezlerini dönme ekseni aldığımız durumlar için hesaplanmış eylemsizlik momentlerini listeyelim.
Uzunluğu L, kütlesi m olan çubuğun merkezine göre:
I = \frac{1}{12}mL^2
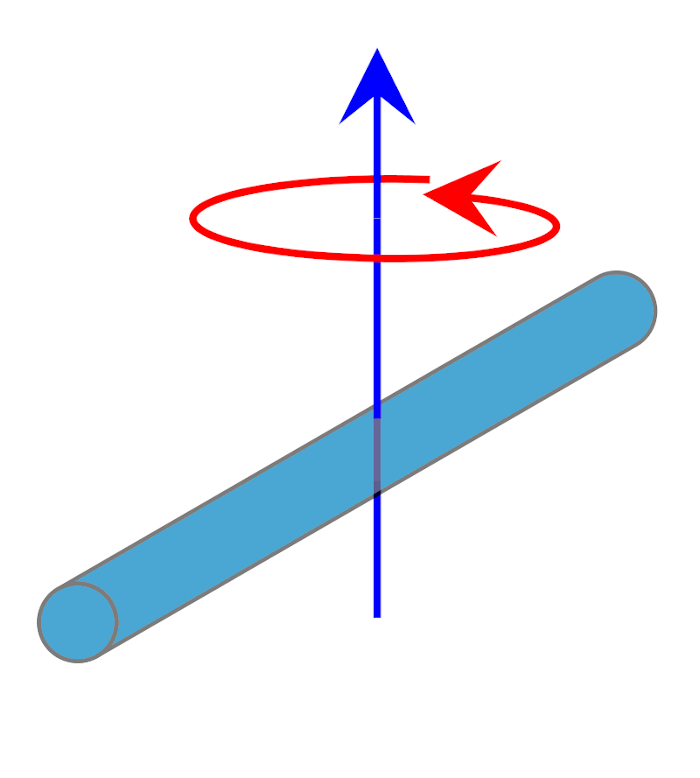
Uzunluğu L, kütlesi m olan çubuğun herhangi bir ucuna göre:
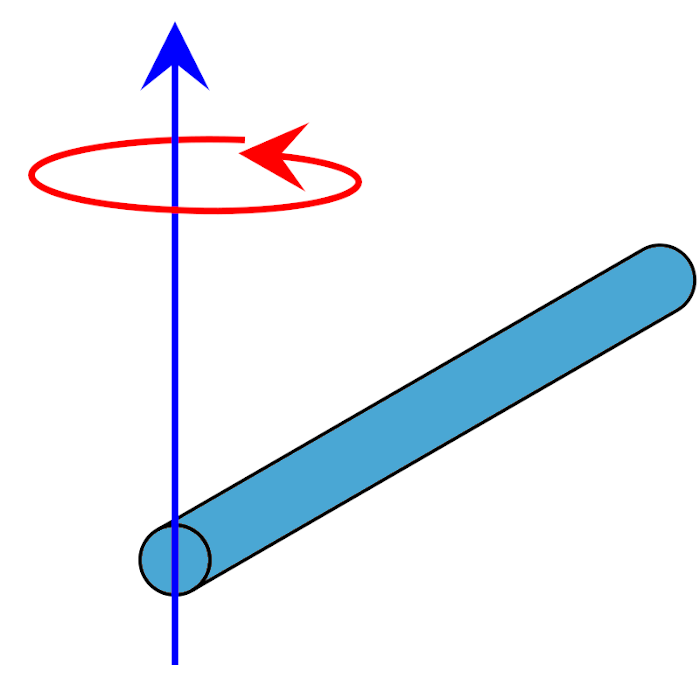
I = \frac{1}{3}mL^2
İçi dolu disk: yarıçapı r kütlesi m:
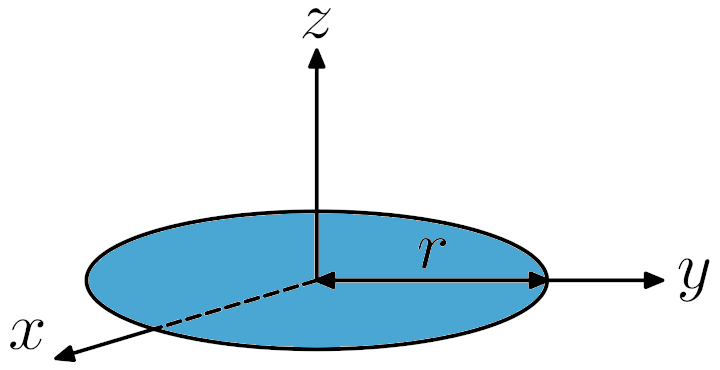
İçi boş ince çeperli silindir:
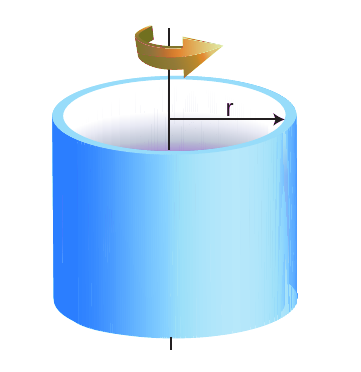
I = mr^2
İçi dolu silindir:
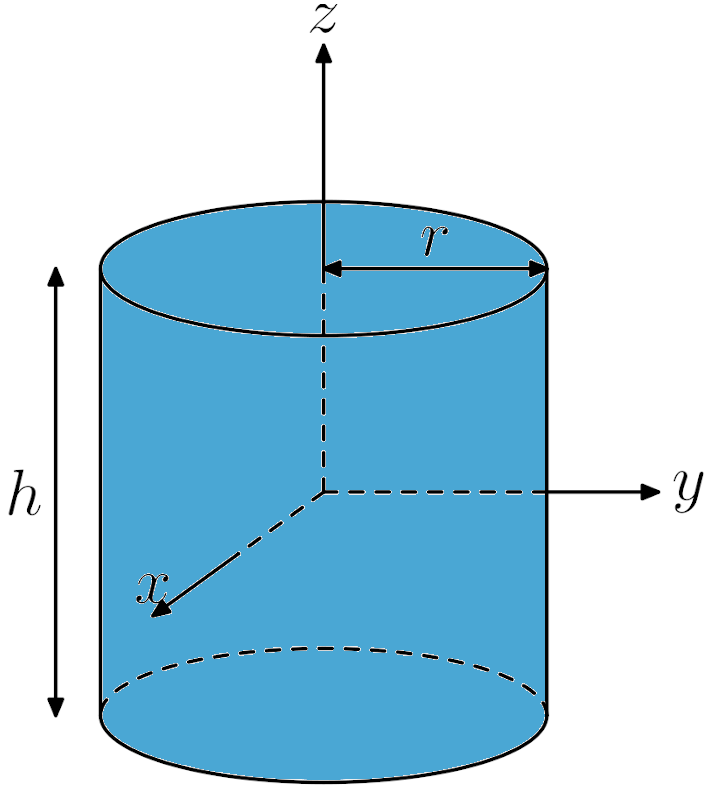
I = \frac{1}{2}mr^2
İçi boş küre:
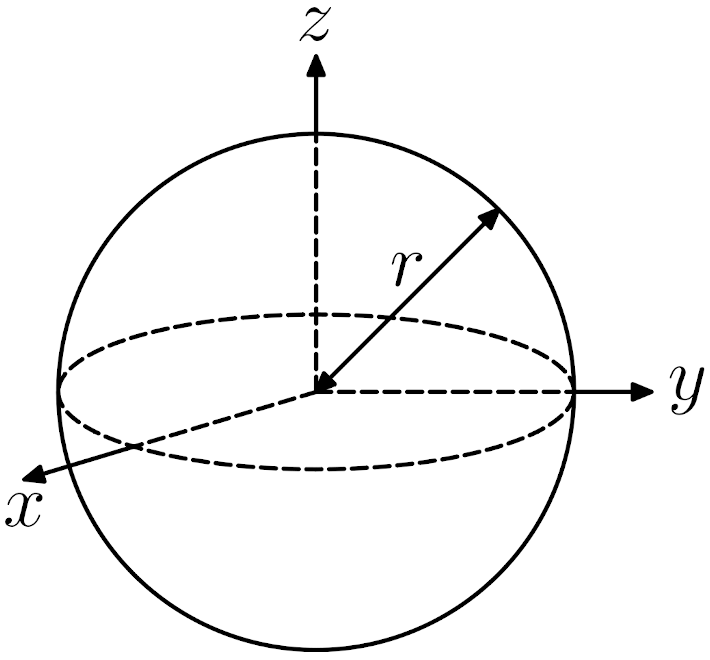
I = \frac{2}{3}mr^2
İçi dolu küre:
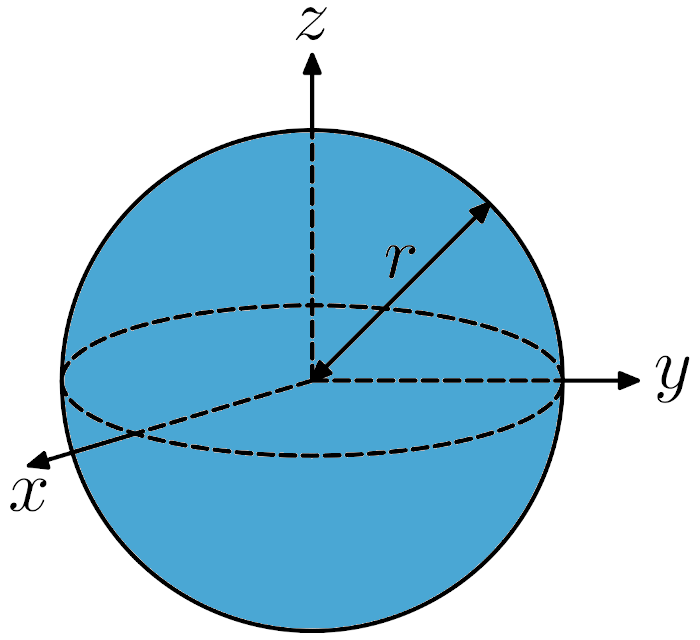
I = \frac{2}{5}mr^2
Eylemsizlik momenti ile ilgili kazanımlar
12.1.2.2. Eylemsizlik momenti kavramını açıklar.
- Eylemsizlik momenti ile ilgili matematiksel hesaplamalara girilmez.
A nın momentını bulurken kırmızı için mr2 mavi için 6mr2 yazılmış, mavi için 6-1 den 25mr2 yazılması gerekmıyor muydu
aynısı B için buldugumuzda da geçerli 6-2 den 16mr2 seklinde olması gerekmıyor mu? çap 6 r yarıçaplar 2 ve 4 r olarak dagılması lazım degıl mı ?
Dikkatiniz harika düzeltildi.