Çıkrık, bin yıllardır kullanılan bir basit makine sistemidir. Çıkrık sistemi iki türlü kurulabilir. İlkinde eksenleri aynı yarıçapları farklı iki silindir bulunur. Bu silindirler aynı ortak eksen etrafında dönebilecek şekilde yerleştirilir. Diğer çıkrık türünde ise bir silindire silindirin merkezine bağlı bir kol eklenir. Günlük yaşamda çıkrık sistemi su kuyularında, el matkaplarında, bisiklet pedallarında ve olta makinesinde kullanılır. Şimdi bir şekil üzerinde çıkrığın özelliklerini inceleyelim.
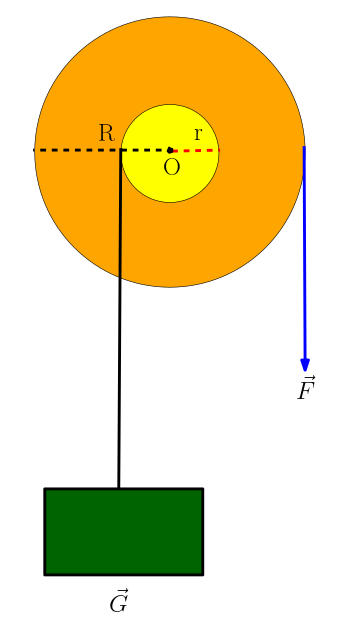
Bu şekilde çıkrığa tam karşıdan bakıyoruz. İçeride sarı renkli ve r yarıçaplı küçük silindir, dışarıda turuncu renkli ve R yarıçaplı büyük silindir var. Ağırlığı G olan cismi küçük silindire bir halatla dolamışız. Büyük silindire uyguladığımız F kuvvetiyle de bu ağırlığı dengeliyoruz. Eğer sistem dengedeyse ki öyle olduğunu söyledik, G ağırlığının ve F kuvvetinin O noktasına göre torklarının eşit olması gerekir:
Gr = FR; \space F = G\frac{r}{R}Çıkrık kolu (yani büyük silindirin yarıçapı) F büyüklüğündeki kuvvetle bir tur döndürüldüğünde halatın sarılı olduğu yük kolu (yani küçük silindirin yarıçapı) de bir tur döner. Demek ki yük, küçük silindirin çevresi kadar yer değiştirir. Çıkrık kolu (büyük silindir) n tur döndüğünde yük h kadar yer değiştiriyorsa, enerji korunumu yasasına göre kuvvetin yaptığı iş, yüke aktarılan enerjiye eşit olur:
F(2\pi R)n = Gh
Sonucumuzu yorumlayalım: Yükün yer değiştirme miktarı (h), uygulanan kuvvete (F), yükün ağırlığına (G) ve çıkrık kolunun uzunluğuna (büyük silindirin yarıçapına) bağlı değildir. Şimdi soru çözelim.
Örnek soru 1
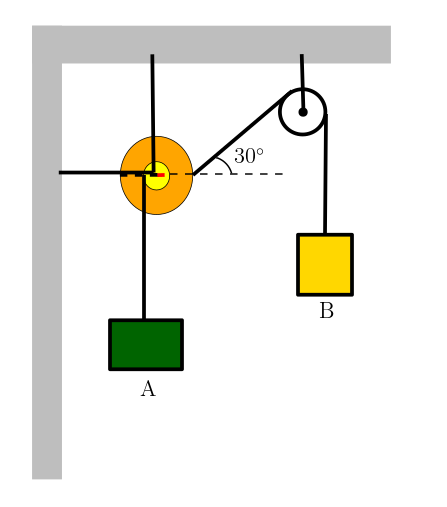
Şekilde gösterilen çıkrık ve sabit makaradan oluşan sürtünmelerin ihmal edildiği sistemde ağırlıkları sırasıyla GA ve GB olan A ve B cisimleri dengededir. Çıkrığın küçük silindirinin yarıçapı büyük silindirinkinin dörtte biri uzunluktadır. Buna göre A cisminin ağırlığının B cisminin ağırlığına oranı kaçtır?
Çözüm
Öncelikle sabit makaralarda kuvvetin büyüklüğünün değişmediğini sadece yönünün değiştiğini biliyoruz. Öyleyse çıkrığın kuvvet koluna (büyük silindire) etkiyen kuvvet B cisminin ağırlığına eşit GB.
Şimdi çıkrığa bakalım. Aşağıdaki şekildeki gibi bu kuvveti de x ve y bileşenlerine ayıralım. GBx bileşeninin yarıçapla aynı doğrultuda olduğunu dolayısıyla torkunun sıfır olduğunu gördünüz mü? Öyleyse bizi sadece kuvvetin y bileşeni ilgilendiriyor GBy.
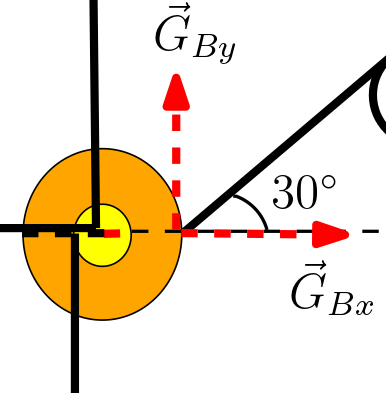
Artık tork denklemimizi yazabiliriz. R = 4r olduğunu biliyoruz. (r küçük, R büyük silindirin yarıçapı). Soruda verilmiş bu bilgi.
G_{By}(4r) = G_A(r)
Bu sistemin mekanik avantajının (kuvvet kazancının) iki kat olduğunu bulmuş olduk.
Örnek soru 2
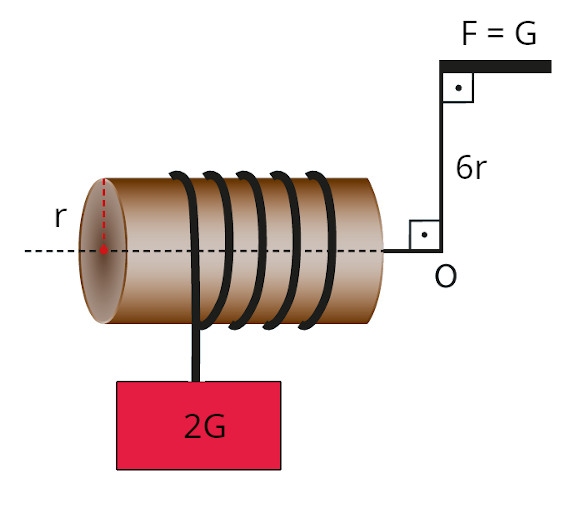
Şekilde gösterilen çıkrık sisteminde ağırlığı 2G olan cisim, G büyüklüğündeki kuvvetle ancak dengelenmiştir. Çıkrığın iç silindirinin yarıçapı r, çıkrık kolunun uzunluğu 6r olduğuna göre bu çıkrığım verimi kaçtır?
Çözüm
Verimin ne olduğunu hatırlayalım. Sistemden alınan enerjinin sisteme verilen enerjiye oranı. Önce çıkrık kolunun yaptığı işi bulalım. Çıkrık bir tam tur döndüğünde çıkrık kolunun çevresi kadar yol alır.
W_1 = G(2\pi)(6r) = 12G\pi r
Şimdi de yük koluna yapılan işi bulalım. Merkezleri çakışık olan bu silindirler birlikte dönüyor. Yani çıkrık bir tam tur attığı zaman yük kolunun çevresi kadar yol alır.
W_2 = 2G(2 \pi r) = 4G\pi r
Artık verimi hesaplayabiliriz:
Verim = \frac{W_2}{W_1} = \frac{4G \pi r}{12G \pi R} = \frac{1}{3} \approx %33.3
Bu pek de verimli bir çıkrık değilmiş.
Çıkrık ile ilgili kazanımlar
11.1.10.1. Günlük hayatta kullanılan basit makinelerin işlevlerini açıklar.
- Kaldıraç, sabit ve hareketli makara, palanga, eğik düzlem, vida, çıkrık, çark ve kasnak ile sınırlı kalınır.
11.1.10.2. Basit makineler ile ilgili hesaplamalar yapar.
- İkiden fazla basit makinenin bir arada olduğu sistemlerle ilgili matematiksel hesaplamalara girilmez.
- Hesaplamaların günlük hayatta kullanılan basit makine örnekleri (anahtar gibi) üzerinden yapılması sağlanır.
- Basit makinelerde verim ile ilgili matematiksel hesaplamalar yapılması sağlanır.